问题

一、设情景—乐寻疑—激发创新欲望。

“问题解决”是一个“让学生在教师的指导下，在教师创设的问题情境中不断进行探索活动的过程”。在这个过程中，我们应重视考虑问题的“原型”，尽可能从生产、生活的数学学习中提炼好的问题，并且要不断创设问题情境，设计探索性和开放性的问题，让学生能独立思考，自己提出问题。

如：学习“圆的面积计算”时，一开始，就故意让学生计算下面四个图形的面积：

学生就会提出：圆的面积计算还没有学，它的面积该怎样计算？在学生主动提问的基础上，提出以下问题让他们继续思考：你知道左、右两个圆哪个面积大？想一想，圆的面积大小到底与什么有关？有什么关系？我们能否像用“割补法”推导平行四边形面积计算公式一样来推导圆的面积计算公式？这样就使学生有产生问题的体验。

又如：学习“角的度量”一课，在认识量角器时，让学生自已观察量角器，问：你发现了什么？你有什么问题可以提？通过观察、思考，有的说：“为什么有两个半圆的刻度呢？”“内外两个刻度有什么用处？”“只有一个刻度会不会比有两个刻度更方便度量呢？”为什么要有中心的一点呢？”等等，学生提出各种不同的看法。在度量形状如“√”时，有的学生提出不必要用其中一条边与量角器刻度线重合的办法。通过教师的精心设计，让学生发现问题、提出问题、敢于提出问题，大大激发学生的创造欲望，让他们学会创造性地思维。

二、给时空—善探疑—激发创新意识。

在“解决问题”的过程中，我们应创设各种解决问题的途径和方法，给学生提供一个充分的创新机会，深入课堂抓住问题，从独探到共探，由小组共探到全班共探，让学生在解决问题中，尝试到探索成功的乐趣，使每个人在教学活动中都得到不同的发展。

如：学习“9加几”时，进行以下数学活动。教师：学校关心小朋友的身体健康，买了好多皮球。一盒装满了是几个，现在盒子里面有多少个皮球（9个）？外面呢？（2个）一共有多少个皮球？（边说边出示图片）

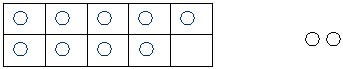
以小组为单位进行讨论。指名回答后，又问：你是怎样知道的？生A：我是一个一个地数，刚好是11个。所以一共有11个皮球。生B：从9个往下数是10，再往下是11个。生C：我先从盒子外面拿1个皮球放到盒子里面，刚好是一盒10个球，再加上外面剩下的1个球，一共有11个球。接着，师提出：这三种方法哪一种最好？为什么？（指名回答）完成“9+2”后，让学生用刚才的方法算一算“9＋8＝（  ）”。这时我们大胆改变例题顺序，把例2的“9+3”改成“9+8”。因为“9+3”与例1情形相近，都是第二个加数偏小，对学生形成发现“凑十法”的意义不大，而选第二个加数是8是开放思维过程的训练，因为8可以分成7和1，6和2，5和3，4和4。为什么计算时只要把8看作1和7呢？再让学生以小组为单位进行探索，激活了学生的思维，在学生心中种下了创新的种子。

又如：学习认识数“6”时，先让学生利用6根小棒摆出自己喜爱的图形，经过学生的动脑、动手、交流合作，摆出以下图形：

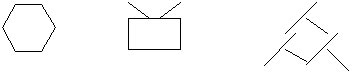
借此机会向学生提问：“6”这个数是由几和几合起来的？用小棒摆一摆、比一比，看谁摆法最多？这时，同学们的积极性更高，个个聚精会神地寻找组成6的几组数。紧接着让同学们互相交流摆的方法，讨论怎样摆得快，这样他们就能按一定顺序排列：

如：

通过学生自己动手操作，互相讨论，大家很快认识了组成“6”的两个数、三个数……直至6个1组成6。

三、给策略—共析疑—提供创新保证。

在析疑时，引导学生积极探索知识，寻求解决问题的策略，使学生建立起一个新的认知结构。师生以创新性为标准，各抒已见，共同评价学生的思维知识，对探索性我们要求学生共同寻求问题解决，使学生建立起一个新的认知结构。师生以创新性为标准，各抒已见，共同评价学生的思维结论，对探索性、开放性的问题树立尊重差异性，追求新颖性的概念，通过发散性的答案引导学生以创新性为标准去评价别人与自己的思维成果。

如：学习“6+7”时，学生通过动脑、思考的方法有：

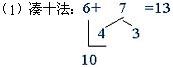（2）调换加数的位置：7+6=13

（3）6+6=12，12+1=13

（4）7+7=14，14-1=13

（5）6+10=16，16-3=13。……

（6）通过规律作答，和的个位比第二个加数少3，就是1个十、3个一合起来是13。

四、课末处—巧留疑—提高创新能力。

在课末，留下富有启发性和开放性的思考问题，它是知识的应用阶段，能给学生极大的思索余地和广阔的探究空间，知识只有在创造性运用中才能产生巨大的力量，也才能超过原有价值。

如：学习“9加几”后，出示以下题目：马路上开来一辆公共汽车，车上坐了几名乘客？还有几人在排队上车？（出示媒体），他们全上车了，车开走了，谁知道现在车上有几名乘客？你是怎么知道？再让学生举出生活中“9加几”的例子。

学习“简单的加减法”应用题后，让学生“唱儿歌，巧算题”：小河水，哗哗啦，一行小鸭水上游。其中有只小花鸭，伸长脖儿嘎嘎嘎。顺着数，它第九，倒着数，它第八。多少小鸭水上游？算对心里乐开花。

在学习“两位数减一位数的退位减法”时，课未设计以下习题：45-（  ）=（  ）、（  ）-6=（  ）、（  ）-（  ）=（  ），要求在（  ）里填上适当的数，使这些算式成为当天学过的习题。

总之，我们在教学中，要尽可能地给学生提供自主探索的机会，让学生主动参与发现问题、提出问题到解决问题的全过程，从而充分发挥自己的潜能，迸发出创造的火花。同时，在探究问题的过程中学会与他人合作、学会表达和交流解决问题的过程与结果，体验解决问题策略的多样性，充分感受到学习数学的实用性。