在困惑中走进新课程

教师在职教育有多种形式,如短期课程培训、单元式工作坊、教学观摩和研讨会等,所有这些形式都要面对理论到实践的转移问题。面对着新课程，如何更好把握新课程理念，逐渐走进新课程呢？下面是我三教《乘法分配律》的体验与感受。

【实践与思考】

【教材分析】乘法分配律是九年义务教育六年制小学教科书的内容，是乘法运算定律中学生最难理解与掌握的内容。学生在运用乘法分配律进行简便计算时，往往出错，其根源就在于没有很好地理解与掌握乘法分配律。依据教材编排的意图，通过用两种方法计算长方形的周长，来说明两种算法都是求一个长方形的周长，结果相同，所以两种算法的算式有相等关系，即（5＋3）×2=5×2＋3×2,，然后让学生通过几组类似的算式的计算，引导学生发现规律,用这样的方法进行教学怎样呢？

一教乘法分配律

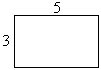1、提供素材一：看图计算长方形的周长（单位：厘米）

（老师根据学生的计算板书两种计算方法，并用等号联接）

2、提供素材二：题组计算、比较。

（12＋8）×5 ○12×5＋8×5

14× (10＋3)○14×10＋14×3

(30＋4)×25○30×25＋4×25

（1） 通过计算，你发现了什么？

（2） 讨论与发现：这三组算式，每组两个算式之间有什么共同的特点？从这些例子里你能发现什么规律吗？

3、引导学生观察、比较，归纳乘法分配律。

发现问题：

1、有部分学生不能用两种方法正确计算长方形的周长，因而这两种方法对于他们来说，就不具有普遍意义。

2、教师提供的素材过于枯燥，限制了良好的自主探索氛围的营造，学生自主探索的热情不高，兴趣不浓，只有部分学生参与，效果不理想。

3、学生用数学的语言来表达乘法分配律，比较困难。

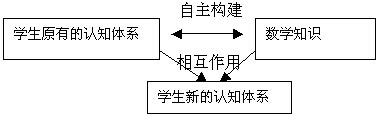
体验与感悟：学生的数学学习过程是一个自主构建自己对数学知识的理解的过程，即他们带着自己原有的知识背景、活动经验和理解走进学习活动，并通过自己的主动活动，包括独立思考、与他人交流和反思等，去建构对数学的理解。用图表示如下：

教学中提供的素材，一是没有充分考虑学生原有的知识背景、活动经验和理解，使部分学生的新旧知识之间出现脱节，二是没有挖掘学生这一潜在的资源，没有让学生从自己的角度提供丰富的素材，因而，不能有效地激发学生自主探索的热情。

自我改进策略：

1、 可以课前通过适当的复习，使所有的学生都掌握用两种方法计算长方形的周长；

2、 是在教师提供素材的基础上，让学生自己举出例子，追求素材的丰富性和多样化，也许可以促进学生数学地思考问题与表达自己的想法。

二教乘法分配律：

1、 课前帮助用两种方法计算长方形周长有困难的学生。

2、提供素材一：看图计算长方形的周长（单位：厘米）

（老师根据学生的计算板书两种计算方法，并用等号联接）

3、 提供素材二：你能举像这样的例子吗？（学生举例，老师板书）

a) 通过计算，你发现了什么？

b) 讨论与发现：这几组算式，每组两个算式之间有什么共同的特点？从这些例子里你能发现什么规律吗？

4、引导学生观察、比较，归纳乘法分配律。

发现问题：

（1） 学生虽然能够很熟练地用两种方法计算长方形的周长，但是学习的热情不高。

（2） 学生举的例子，大部分是模仿的，因而观察与探索规律的兴趣不浓，用数学的语言来叙述，仍然困难多多。

体验与感悟：为什么从学生原有的知识水平出发，通过学生自我举例，在此基础上引导学生观察比较，仍难以达到预计的教学效果呢？从这两节课看来，学生对于像长方形周长计算这样的素材兴趣不大，学生对怎样的素材感兴趣呢？研究表明：每个学生都有分析、解决问题和创造的潜能，关键是要为儿童提供那些对学生来说具有现实的、与生活实际相联系的素材，要重视学生的直接经验，重视第一手材料，为学生的数学学习提供具体形象的认识支柱。

自我改进策略：

1、 通过实践活动为学生积累第一手感性材料；

2、 从与学生生活实际相联系的角度选取素材；

3、 可鼓励学生用适合自己的认知方式来表达对乘法分配律的理解。

三教乘法分配律：

1、课前调查。分成若干小组，对扬子广场的部分食品的单价进行调查，如下表：

思考一：任选其中两种食品，购买的数量一样时，一共用要付多少元？你能编一道这样的应用题吗？

思考二：你能用两种方法来解答吗？

2、提供素材。

（1） 老师提供富有情境性的素材。如图：

启发讨论：如果一个同学只会用其中一种方法解答，你能帮助他学会第二方法吗？

指导观察比较：这两个算式什么地方发生了变化？

（2） 学生自主提供富有生活气息的类似于这样的实例。

要求：你能向同学们解释你是怎样解决的吗？

3、引导学生观察、比较，归纳乘法分配律。

你能发现其中的规律吗？可以用不同方式来表示：如用语言、动作、字母等方式来表示你的发现。

通过课堂教学实践发现：

（1）学生通过课前的实践调查活动，能够熟练地任选其中两种食品，构建类似于这样的应用题：今天我去扬子广场买食品，牛排每袋3元，鱼排每袋2元，牛排和鱼排各买4袋，我一共要付多少元？并且能够熟练地运用两种方法进行解答。

（2）学生极其认真地教他人学会用第二种方法进行解答。

（3）学生提供了极其丰富且多样化的实例，如购买食品、相遇应用题中求路程的问题、求长方形的周长等等。

（4）学生在探索乘法分配律的时候，用不同的方式表示了对乘法分配律的理解，如有的学生用手势，有的学生用语言加手势来说明，而有的学生则擅长于用字母来表示，有的学生则用符号来表示：（○＋□）×◎＝○×◎＋□×◎……表示的方式丰富多彩，极具情趣，使课堂上处处洋溢着和谐的气氛。

体验与感悟：

一、对于小学生来说，具有现实意义的、与生活实际相联系的内容，更易数学化。

走进新课程，实施新课程改革，数学教学就必须面向学生、面向自然、面向社会、面向实际。其实实践一直是数学发展的丰富源泉，数学脱离了现实就会变成"无本之木""无源之水"。著名数学家J.V.Neumann早在1947年就说过："远离了它的实践的源泉之后，或者太多'抽象'的近亲繁殖之后，数学学科就处在退化危险之中。在开始的时候，款式通常是经典的；当它有迹象表明成为巴洛克式时，那么，危险的信号就升起了。" 从小学生学习数学的认知、情感发展的阶段性特点来看，小学生更多地关注"有趣、好玩、新奇"的事物。因此，学习的素材的选取与呈现以及学习活动的安排都应当充分考虑到学生的实际生活背景和趣味性，使他们感觉到学习数学是一件很有意思的事情，从而愿意接近数学。案例三的改进之处，就在于它为学生探索乘法分配律提供了丰富的来源于学生生活实际的素材：通过课外调查，了解扬子广场的部分食品的价格；通过购买蓝球和排球各5只，进一步地唤醒学生元认知；通过腾出时空，让学生自由列举生活的实例，强化数学与生活的联系。有这样丰富的取材于学生生活实际的素材，就为学生进一步地探索规律奠定了良好的认知和情感基础，提供机会让学生经历"从具体情境实例符号化"，即让学生在不知不觉中经历数学化的过程。

二、对于小学生来说，富有情趣的、挑战性情境，更易兴趣化。

案例二中，为什么基于学生原有认知基础上的自主探索，仍然没有出现学生的数学学习活动应当是一个生动活泼的、主动的和富有个性的过程场面呢？我们不妨把案例二与其它两个案例进行比较，案例二与案例一比较，改进的是发现学生原有认知存在缺陷，因而课前采取了补救措施，案例二与案例三比较，案例二注重的是从大量的等式中，引导学生抽象概括出乘法分配律，它缺少的是案例三中每一个等式都蕴含着学生对它独有的情趣（因为案例三中每一个等式都是学生从他们各自经历的生活中挖掘出来的）。在数学课程目标的改革中，《标准》对"过程"赋予了更为深刻的含义，明确了"过程"的定位：过程本身就是一个课程目标，即首先必须要让学生在数学学习活动中去"经历……过程。" 但经历过程不单单是为了一些结果，如案例二中通过举出一些等式，引导学生探索乘法分配律，这样一个过程关注更多的似乎是乘法分配律这个结果。而案例三中课前调查，分成若干小组，对扬子广场的部分食品的单价进行调查，然后思考与尝试：任选其中两种食品，购买的数量一样时，一共用要付多少元？你能编一道这样的应用题吗？你能用两种方法来解答吗？作为一个调查，这中间似乎并不含有多少确定性，但学生通过一个充满探索、思考和合作的过程学习数学，获取知识，收获的将是自信心、责任感、求实态度、科学精神、创新意识、实践能力，这些远比一个结果更为重要。从这富有情趣、挑战性的情境中收集来的素材，无一不包含着学生个体独特的情感与感受，也正是这些富有情感化的素材，当学生对这些素材进行观察比较、抽象概括、演绎推理时，学生更带有倾向性、专注性与主动性，无论探索的结论是否正确，都能进一步地激发怀孕与培养学生学习数学的兴趣，强化学生数学学习积极的情感与养成良好的学习数学的态度。

三、 对小学生来说，富有个性地学习数学，更易情感化。

案例三与其它两个案相比较，其改进之一也在于：让学生用自己擅长的方式来表示自己发现的规律：可以用语言、可以用动作、可以是语言加动作，也可以是字母、符号等等。从课堂教学实践反映的情况看，学生用了很多种表示的方法，有的学生甚至用：（单价1＋单价2）×数量=单价1×数量＋单价2×数量来说明乘法分配律的意义。与单纯地用数学的语言来表达乘法分配律相比较，在这节课上学生个个眉飞色舞，课堂氛围轻松而热烈。这又是为什么呢？人的智力结构是多元的，有的人善于形象思维，有的人长于计算，而有人的擅长逻辑推理……。另外，每个学生都有自己的生活背景、家庭环境和一定的文化感受，从而导致不同的学生有不同的思维方式和解决问题的策略。因此，对于同样一个数学知识，学生理所当然地可以从他们各自的角度去理解、去感悟、去内化。因而，我们的数学教学就必须尽可能多地让学生经历数学交流活动，使得学生能够在交流活动中感受别人的思维方式和思维过程，在相互交流中，相互补充，相互接纳，不断创新，共同提高，使学生经历"从具体事物学生个性化学习学会数学"这样一个过程。学生这种富有个性的数学学习过程，使看似单调的数学知识与学生原有的丰富多彩的元认知有机地结合在一起，使数学知识更具情感化、生命化。

作者简介：

彭德春，男，1969年1月生，教龄17年，小学高级教师，本科学历，任教小学数学。

邮编：213341 电话：0519－7521152；7522694