小学数学考试命题改革的尝试与探索

那么，新课程下的评价试题为什么要发生变化呢？作为教师和家长应该如何把握新的命题方向，有的放矢的辅导学生迎接考试呢？我们龙亭区教研室在这方面做了一系列的探索和尝试，并积累了一些经验和体会。

首先，我们认为新课程标准下试卷命题的主要意图，是考察学生是否具有数学意识和综合应用数学知识解决实际问题的能力。

数学意识包括：（1）数学是客观存在的，数学知识在我们的生活中无处不在，我们生活中的各个方面都离不开数学知识。（2）数学知识是有用的，数学知识是为解决生活中的问题服务的。因此，现在的试题在选材上要拉近数学与学生生活的距离，多选取一些学生感兴趣的、学生身边的事例，让学生感受到数学知识的存在，感受到数学知识的价值。

综合数学知识解决实际问题的能力包括：（1）发现数学问题的能力，凭借对数学问题的敏感，能发现隐藏于现实生活之中的数学问题；（2）提出数学问题的能力，具有一定的数学头脑，能够从数学的角度分析和解决生活中的问题；（3）收集信息的能力，能够在现实生活中通过各种渠道收集解决问题所需要的各种信息；（4）信息处理能力，能够在繁杂的各种信息之中，筛选出对解决问题有用的信息；另外还有灵活解决问题的能力等等。因此，现在的试题所提供的信息不像原来那样整齐、有序，变得有些零乱、内隐，需要学生对信息重新组合、筛选，目的就是考察学生综合数学知识解决实际问题的能力。

那么，怎样能够在试题中培养学生的数学意识和综合运用数学知识解决实际问题的能力呢？我们在考试命题实践中从以下几个方面进行了初步的探索和尝试。

一、试题选材上的变化

1. 现实性：试题选取一些学生生活关系密切的题材，或创设一些学生生活中的一些情境，拉近数学知识与学生生活的距离。

A、选取学生身边熟悉的事物作题材。

如例1：我国的国旗是按照一定的长宽比例制成的，阳光小学校园内飘扬的五星红旗长144厘米，宽96厘米，那么，国旗的长与宽的最简单的整数比是（ ）。

B、创设一些现实的情景作题材。

例2：小明和小军进行滚铁环比赛，最后小明输了。小明对小军说：“主要是因为你的铁环的直径是我的2倍，所以你的铁环滚1圈，我的要滚4圈才追上你”。小明说的对吗？

C、选取一些新闻大事作题材。

例3：“神舟6号”载人飞船原来设计的重量约是11500千克。我国科学家在实际制造飞船时使用了碳纤维复合材料，这样飞船的重量就比原来减轻了30% 。请你算一算，现在“神舟6号”载人飞船的重量是多少千克？

2. 知识性：学生既解决了数学问题，又能获得其他方面的知识，考有所得，这更符合新课程标准所倡导的评价改革中的发展性原则。

例4：地球上的物质，大都会热胀冷缩。但水结成冰以后，体积却增加 1/10。现在有一块冰，体积是3.3立方米，请你算一算，它融化后的体积是多少立方米？

3. 教育性：新课程标准特别关注对学生情感、态度和价值观的培养，因此，试题可以选取一些对学生有教育意义的题材。

A、环境保护的教育

例5：根据以下信息提出一个数学问题并解答。资料显示，我国森林草地破坏形势不容乐观。20世纪的50～90年代间，西双版纳热带雨林消失了1/3，解放初期海南岛森林面积有8 4万公顷，可现在海南岛的天然林面积只有解放初期的1/4。我国现有退化草地135万平方千米，约占我国可利用草地面积的1/3。

B、节约用水的教育

例6：我国是世界上13个人均水资源最贫乏的国家之一。2005年世界人均拥有淡水资源量为9200立方米，而我们国家人均拥有量仅为世界平均水平的1/4，在扣除一些难以利用的水资源后，我们国家实际人均可利用的淡水资源只占到拥有量的9/23。（1）根据以上信息，请你求出我们国家实际人均可利用的淡水资源量是多少立方米？（2）看到本题的有关信息，你有什么想法？请你简要谈一谈。

4. 探索性：试题的考察不是停留在记忆和判断的层面，而是要求学生在自己学到的知识的基础上，进行一些尝试和探索，然后找到解决问题的方法。

例7：根据下表中的数据判断哪一种水果含的水分多？ （ ）

A.苹果 B.葡萄 C.一样多

试题的呈现形式改变了过去的纯文字描述，变得丰富多样：

1. 表格。如例7

2. 图画。如例8

3. 对话。如例9

4. 图形。如例10

5. 文字。如例1～6

三、试题强调对信息的选择和判断

如例8：

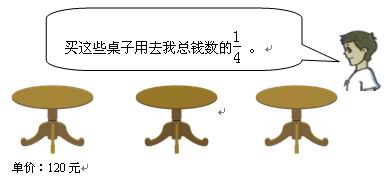
算一算他剩下的钱还能买多少张这样的桌子？

在这一道题中，桌子的个数这个信息是用图画的形式呈现的，需要学生根据要解决的问题从图中收集出来，而桌子的单价这个信息可以有选择的使用，如果选用简单的方法，它就是一个多余信息了。

四、试题的开放性

新课程标准强调“不同的人在数学上有不同的发展”，学生的年龄不同、生活背景不同、知识经验不同，思考问题的角度和解决问题的方法也会个性化和多样化。

1. 解决问题策略的开放性

（1） 如例9：根据以下信息求出五年级一共要种多少棵树苗？

小红：五年级的三个班参加植树活动。

小明：我们五(1)班种了树苗总数的3/10，

小玲：我们五(2)班种了100棵，

小华：我们五(3)班种棵数的比五(2)班多 ，

老师：五(1)班和五(2)班刚好种了树苗总数的一半。

这道题可以从两个角度考虑：

A、根据“我们五(1)班种了树苗总数的3/10”和“五(1)班和五(2)班刚好种了树苗总数的一半”，先求出五(2)班种了树苗的几分之几，再求出所求问题。

B、根据“我们五(2)班种了100棵”和“我们五(3)班种棵数的比五(2)班多 ”，先求出五(3)班种的棵数，再求出“五(3)班种了树苗的几分之几”，最后求出所求问题。

2. 答案的开放性

如例10：下图是一张圆形纸片，圆中间画一条线段，你能判断这条线段是不是该圆形纸片的半径吗？请把你判断的方法简要的写出来。

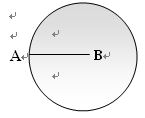
这道题判断的方法有很多种，比如：

（1）假设B点是圆心，AB是圆的半径，以B点为圆心，AB为半径画圆，看得到的圆是不是现在的圆。

（2）将圆形纸片对折几次，看得到的圆心是不是在B点处。

（3）过B点做AB的垂线，看看到的两条“半径”是不是和AB一样长。

（4）延长AB交于圆上的点C，看看AB和BC是不是一样长。