在数学教学中培养学生的创新思维

一、创设问题情境，激起创新欲望

心理学告诉我们：在人的心灵深处，都有一种根深蒂固的需求，那就是希望自己有朝一日成为一个发现者、研究者或探索者。在数学教学中，教师应该经常有意识地创设一些问题情境，把学生这种潜在的需求激发出来，使之产生创新的欲望。

例如，教学“圆的周长”时，教师设计如下矛盾冲突：用直尺直接测量一个圆的周长，你能不能想出一个好办法来？（生1：把圆放在直尺边上滚动一周，用滚动的方法测量出圆的周长；生2：用绳子在圆上绕一周，再测出绳子的长短，得到这个圆的周长）。随后，教师甩动绳系小球，形成一个圆，问：小球运动形成一个圆。你能用刚才的方法测量出圆的周长吗？（学生面面相觑，面露难色）于是，教师抓住时机：“看来，用滚动、绳绕的方法可以测量出圆的周长，但却有一定的局限性。我们能不能探讨出求圆周长的一般方法呢？”学生一下活跃起来，并经过讨论和教师的引导，很快就得出求圆周长的一般方法。通过教师施问创境，诱发学生主动参与问题解决的“再创造”过程，这样，就激起了学生的兴趣和探究的强烈愿望。

二、引导猜想，培养创造性思维能力

猜想是一种创造性思维活动，它可导出新颖独特的思维成果。在数学课堂教学中，教师要引导学生勤于猜想，敢于猜想，善于猜想，鼓励学生思考，让他们自由想象，从而达到培养学生的创造性思维能力。

1．通过猜想，培养思维的独创性。

现代教学是发生在教师和学生之间互相传输信息的过程，因而在教学方法上，教师必须最大限度地调动学生的学习积极性，鼓励他们“标新立异”，激发他们猜想更好的方法。

例如，计算8＋98＋998＋9998＋99998＝？若采用逐项累加法，结果非常繁琐。若引导学生猜想将8分解成2＋2＋2＋2，然后利用加法交换律和加法结合律进行计算，即原式＝2＋2＋2＋2＋98＋998＋9998＋99998＝（2＋98）＋（2＋998）＋（2＋9998）＋（2＋99998）＝100＋1000＋10000＋100000＝111100，很快就得出了式题的计算结果，让学生体验到学习的乐趣。这样，通过充分引导学生大胆猜想，激发了学生的学习兴趣，同时也培养了学生思维的独创性。

2．通过猜想，培养思维的发散性。

发散思维是创造思维的重要组成部分。它不受一定的解题模式的束缚，从问题个性中探求共性，寻求变异，沿着不同方向，不同角度去猜想、延伸、开拓。在数学教学中，一般可采用一题多解的训练，培养和锻炼思维的发散性。

例如，李军家与学校之间的距离是1020米，李军3分钟走255米，照这样计算，李军到学校还需几分钟？启发学生用不同的思考方法探解。

解法1：求李军到学校还需几分钟，就是求余下的路程所需的时间。“从3分钟行255米”，可求出李军速度为255÷3，而余下的路程是（1020－255），然后根据“路程÷速度＝时间”得出：（1020－255）÷（255÷3）＝9（分钟）。

解法2：求李军到学校还需几分钟，也可先求李军走完全程的时间，然后减去已行路程的时间，即得到余下路程的时间1020÷（255÷3）－3＝9（分钟）。

解法3：用倍比法解，将已行的路程255米看作“1”倍数，全程1020米是已行的255米的4 倍，行255米用3分钟，那么行完全程1020米就得用12分钟，然后减去已行的时间，即得出：3×（1020÷255）－3＝9（分钟）。

通过上述的练习，引导学生从多种角度，不同方向思考问题，这不仅能提高学生灵活运用知识的能力和解题技巧，而且可以发挥学生的独特见解，促进思维发散性的发展。此外，一题多变、一空多填等训练，同样也能培养和锻炼学生思维的发散性。

3．通过猜想，培养思维的灵活性和敏捷性。

“好动、好想、好奇”是学生共同具备的心理特征。教师应抓住学生这一心理特征，鼓励学生大胆猜想，使学生自觉地沟通数学知识的纵横联系，挖掘隐含条件；巧妙地构造某个数学对象，迂回转化；灵活地运用各种思维方法和方式，找出解题的各种途径。

例如，求下图的周长（单位：cm）

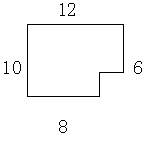
若此题仅会运用周长定义把每条边长相加：10＋12＋6＋8＋（12－8）＋（10－6）＝44（cm），这就显得思维呆板了。若能猜想到将原多边形添上辅助线转化成一个长方形。如图：

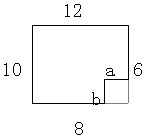
原线段a和b的长度就是两条辅助线的长度，这时只需采用长方形周长计算公式进行运算，就能得到本题的结果，即（12＋10）×2＝44（cm）。

三、提倡质疑问难，培养创新精神

学起于思，思源于疑，疑是点燃学生思维的火种。学生发现问题，大胆怀疑，探果索因，追根问底，是他们创新的开端。在课堂教学过程中，要注重学生的思考过程，启发学生多方面思维寻求正确结论，引导学生对信息自主的加工，鼓励学生质疑问难，激发他们主动创新的精神。

例如，在教学“分数的初步认识”时，有这样一道题：请你表示下面这个正方形的1/4？没过多久，全班出现了好多种表示方法，如：

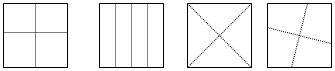
这时，老师就问：还有不同的表示方法吗？学生一听，还有别的表示方法，有的表示怀疑，有的试着找其它方法，过了一会儿，有学生站起来说：“只要固定正方形对角线的交点，旋转两条对角线就能把这个正方形平均分成四份。”话音刚落，很多学生说，这是不可能的，这时，老师因势利导，让同学们按他的方法试一试。结论是一样的。通过这样的教学，保护了学生大胆猜想的积极性，教给了学生探究新知的方法，激励了学生的创新精神。

总之，数学课堂教学是实施素质教育的主渠道，教师必须树立现代的教学观，引导学生自主学习，培养其创新思维，以适应新时代科学知识迅速发展的需要。