中国数学网

美丽的“陷阱”

在一次小学数学毕业测试中，有这么一道应用题：“有一个啤酒厂为了回收空啤酒瓶，规定每3只空啤酒瓶可以换1瓶啤酒。一天，李师傅买了两箱啤酒共24瓶，喝完之后拿空瓶换啤酒喝，李师傅最多可以喝到多少瓶啤酒？”测试完毕，引起老师们的争议：有些老师认为李师傅最多可以喝到35瓶啤酒；有些老师认为李师傅最多可以喝到36瓶啤酒。老师们各抒己见，众说纷纭，正确答案到底是多少呢？下面我们不防先撷取不同思维层次学生（随机取样）的一些解题方法，以飨同行！ 初始水平学生的解题方法： 方法1：24÷3=8（瓶酒）方法2：24÷3+24=32（瓶酒）方法3：24÷3=8（瓶酒）；8÷3=2（瓶酒）……2（个空瓶）； 8+2=10（瓶酒）方法4：24÷3=8（瓶酒）；8÷3=2（瓶酒）……2（个空瓶）；（2+2）÷3=1（瓶酒）……1（个空瓶） 8+2+1=11（瓶酒） [通过对一个学校的学生进行卷面随机取样抽查（以下呈现的数据方法同样），发现用以上四种解题方法解题的学生占抽查总数的33.6%，再通过事后与部分学生的交谈，在他们的思维领域中，解决“李师傅最多可以喝到多少瓶啤酒？”这个问题时，这部分学生有些忽略了原装的24瓶酒，有些没有形成空瓶循环换酒的思维策略。] 中等水平学生的解题方法： 方法1：24÷3=8（瓶酒） 8÷3=2（瓶酒）……2（个空瓶） 24+8+2=34（瓶酒）方法2：24÷3=8（瓶酒） 8÷3=2（瓶酒）……2（个空瓶）（2+2）÷3=1（瓶酒）……1（个空瓶） 24+8+2+1=35（瓶酒）最后余2个空酒瓶，不够换1瓶啤酒。方法3：24+24÷3+（24÷3+1）÷3=35（瓶酒） [这部分学生在解决“李师傅最多可以喝到多少瓶啤酒？”这个问题时，已经初步具有空瓶循环换酒的策略意识以及李师傅最多可以喝到的啤酒瓶数应该包括原装的24瓶啤酒，只是在最关键处即换剩2个空啤酒瓶时不懂得如何去取舍（包括我们部分教师在内），这也是教师们激烈争论的问题焦点。通过调查统计，运用这种解题策略的同学约占抽查总数的 28.7%。] 思维水平比较高的学生的解题方法： 1×12+24=36（瓶） [这种思维的学生用24个“○”表示24个空啤酒瓶。第一次先用3个空啤酒瓶换得1瓶啤酒，喝完换来的这瓶啤酒后再另外拿两个空啤酒瓶凑够3个空酒瓶又换得1瓶啤酒，依此类推，每次喝完就换，一步一步记下喝过的啤酒瓶数，当喝完换来的第11瓶啤酒时，与余下的1个空啤酒瓶加上借来的1个空啤酒瓶，又可以换得第12瓶啤酒，喝完第12瓶啤酒后再去还瓶子,因此最后得出李师傅最多可以喝到36瓶啤酒。] 方法2：喝完两箱啤酒（共24瓶）后，第一次换啤酒： 24÷3=8（瓶酒）；喝完第一次换来的8瓶啤酒后进行第二次换啤酒： 8÷3=2（瓶酒）……2（个空瓶）喝完第二次换来的2瓶啤酒后，加上余下的2个空瓶，进行第三次换啤酒：（2+2）÷3=1（瓶酒）……1（个空瓶）喝完后有一个空瓶+余下的1个空瓶=2个空瓶此时剩下2个空啤酒瓶。李师傅可以向亲戚、朋友、邻居、厂家或商店借一个空啤酒瓶，凑够3个空瓶，然后换得一瓶啤酒，喝完之后再去还瓶子；或者李师傅在商店当场喝啤酒并马上退瓶子。 24+8+2+1+1=36（瓶酒） [从这个思维角度思考的学生，通过一步一步的记下每次换得的啤酒瓶数，当最后换剩两个空啤酒瓶时想尽一切办法先“借”后“还”，因此最后得出李师傅最多可以喝到36瓶啤酒。] 方法3：24÷3=8（瓶酒）（8+1）÷3=3（瓶酒）先从别处借来1个空瓶 3÷3=1（瓶酒）喝完这瓶酒后再去还瓶子 24+8+3+1=36（瓶酒） [喝完两箱啤酒（共24瓶）后，第一次换得8瓶啤酒，喝完换来的8瓶啤酒后，此时李师傅可以先借来一个空啤酒瓶，凑够9个空瓶，然后又换得3瓶啤酒，当又喝完换来的3瓶啤酒后，最后用这3个空瓶换1瓶啤酒，喝完这瓶酒后即可还瓶子] [不管是用“○”图形表示空啤酒瓶（方法1）；还是通过一步一步的推理（方法2、方法3），这部分同学思考的角度都是想方设法先“借1”后“还1”的解题策略，最后才得出李师傅最多可以喝到36瓶啤酒。通过调查统计，运用这种解题策略的同学约占抽查总数的9%。] 方法4：假设空啤酒瓶为a，瓶中酒为b。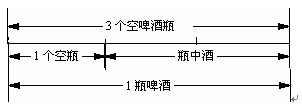 3a=a+b 2a =b 24+24÷2=36（瓶酒）方法5： 24+24÷（3-1）=36（瓶）方法6：由空啤酒瓶换啤酒的规定：每3只空瓶可以换1瓶啤酒，可以知道每3只空瓶可以换一只空瓶和一只瓶子里的啤酒。这就相当于用2只空瓶换一瓶啤酒（不含酒瓶），算式：24+24÷2=36（瓶酒） [用字母表示（方法4）、用线段图表示（方法5）、用语言叙述（方法6）这三种解法的学生，他们思考的角度都是先找出3只空瓶换一瓶啤酒的对应关系即用2只空瓶换一瓶啤酒（不含酒瓶），然后用一一对应的除法求得李师傅最多可以喝到36瓶啤酒。通过调查统计，运用这种解题策略的同学约占抽查总数的6%。]以上撷取的是不同思维水平的学生比较有代表性的解题策略，同时展示了部分学生最原始的思维过程（检测完毕后进行的部分同学交谈和随机抽样的卷面分析），学生有最初的理解策略，即认为“李师傅最多可以喝到8瓶啤酒、10瓶啤酒、11瓶啤酒、32瓶啤酒；逐步过度到35瓶啤酒和36瓶啤酒”，他们在理解题意时有的借助“○”图形、有的借助“线段图”、有的借助a、b等字母符号、有的通过动手画一画、动手摆一摆、一步一步的记下喝过的啤酒瓶数，有的丢掉了思维“拐杖”，直接上升到语言表述，总而言之，学生经历了具体到形象，直观到抽象的思维过程，最终形成自己的解题方法和策略。下面谈谈老师们激烈争议的问题焦点：第一种意见认为：李师傅最多可以喝到35瓶啤酒。理由是：题目中没有说明可以借啤酒瓶，并且向亲戚、朋友、邻居、商店老板借酒瓶或者说在商店当场喝啤酒后马上退酒瓶都是不现实的举措，通俗的讲在现实生活中是难以实现的。所以当最后换剩2个空啤酒瓶时，不符合“每3只空啤酒瓶可以换1瓶啤酒”的规定，理应“忍痛”舍去2，因此李师傅最多可以喝到35瓶啤酒。第二种意见认为：李师傅最多可以喝到36瓶啤酒。理由是：题目的问题是“李师傅最多可以喝到多少瓶啤酒？”问题强调的是“最多”。并且条件是喝完两箱啤酒（共24瓶）之后拿空瓶换啤酒喝。在不再多花钱（或不负债）的基础上，不管用什么方法（先借“1”后还“1”或者……），只要能求出李师傅最多可以喝到的啤酒瓶数即可。所以第二种意见的老师以及笔者本人赞成李师傅最多可以喝到36瓶啤酒的几种解题策略。《数学课程标准（修改稿）》提出：“有效的数学教学活动是教师教与学生学的统一，学生是数学学习的主体，教师是数学学习的组织者与引导者。因此学生的学习应当是一个生动活泼的、主动的和富有个性的过程，除接受学习外，动手实践、自主探索与合作交流也是学习数学的重要方式……”尤其是“合作交流”是针对当前时代和社会对人才综合素质能力的需求提出的，而笔者认为本题向“亲戚、朋友、邻居或商店老板借一个啤酒瓶”，正是“合作交流”这个教学理念在社会生活中的具体体现与检测学生运用所学知识解决实际问题的综合能力，反映我们所培养的学生是否具有“与人合作、与人交流”的人际交往能力。并且我们的学生接触的学习内容是现实的、有意义的、富有挑战性的，所以当学生形成解决问题的一些基本策略后，更应进一步体验解决问题策略的多样性，解题策略的开放性和思维的灵活性和广阔性。题中隐藏有一个美丽的“陷阱”，即当最后剩下2个空啤酒瓶时，是“借1”还是“弃2”呢，这是本题的关键所在，也是问题争论的焦点，同时也彰显我们所培养的学生是“循规蹈矩，不敢越雷池半步”还是“思维开阔、富有创新精神呢”，从侧面也反映我们一部分教师对课改新理念的理解比较滞后。从上面呈现的数据可以发现，处于初始理解水平的学生大约占了33.6%，他们对于题意的理解比较困难，所以这部分学生基本上没有考虑到原装的24瓶啤酒，或者没有形成空啤酒瓶循环换酒的策略意识，所以我们的教师在教学中，要注意引导学生借助图形、符号、线段图以及让学生动手画一画、动手摆一摆或者一步一步的记下换酒瓶数、一步一步的进行推理等策略来帮助不同思维层次的学生对题目的理解，同时要注意鼓励与提倡解决问题策略的多样化，要注意尊重学生在解决问题过程中所表现出的不同思维水平，并且教师对数学问题的设置要力求具有启发性、探索性、发展性、挑战性，设计一些思维含量比较高的问题，从而激发学生的学习热情和主动探索的精神，培养学生对信息材料的处理和对问题的合情推理能力以及灵活应变能力，让学生的综合素质得到应有的发展，成就数学教学的有效性和高效性。