【摘要】真实的课堂不存在完全正确的答案,课堂中的错误往往是学生最朴实的想法,其中蕴含着对问题的思考,也不乏智慧的闪光点。对于学生在课堂上出现的错误,作为21世纪的教师不能急于解释、下定论,而是要把错误抛还给学生,引导他们从正反不同角度去修正错误,给他们一些研究争论的时间和空间;更应该凭借着教师的教学机智,应时制宜,积极应变,善于将学生的 “错误”合理利用起来,挖掘“错误”中合理的成份,从而让学生在争论中分析、反驳,在争论中明理,在争论中内化知识。
【关键词】错误 制造 引出 将错就错 善待
走进新课程,教学的最高宗旨和核心理念是“一切为了每一个学生的发展”。在以“一切为了学生的发展”为基本理念的新课程实施之际,一个老生常谈的话题——学习错误,我们应该站在新的视角对其“价值”进行重新定位,对其进行新的探索和实践,这将是很有意义的尝试,它的最终受益者无疑将是学生——使学生得到积极主动、生动活泼的发展。教学时教师往往原本在思维程序中早已准备好的一份标准答案,突然从“半路上杀出个程咬金”,这样突如其来的插曲往往令教师有些措手不及。因害怕学生会再说出些什么“稀奇古怪”的错误观点,教者便阻挠、制止学生,并且不假思索地将学生本来正确的观点定性为“乱说”,最后,甚至强制性地将学生按在了座位上。这种对学生犯错畏之若虎的态度却恰恰掩盖了学习本来的面目,违背了课改的初衷,也掩盖了学生真实的思维活动。敢于冲破教师设置的思维围墙,充满自信地“固执己见”引经据典,这需要多大的勇气呀!我们怎能不为之喝彩?为孩子的勇气喝彩,也为其中闪现出来的亮丽的思维创新的火花喝彩,这就是“错误”成为数学课堂教学的一个亮点吧!怎能不倍加珍惜呢!
一 制造错误,争中分析
在课堂教学中教师将错误制造,让学生在“尝试错误”中比较、分析、甚至引发争议;让学生从分析错误中学会反思,深化了对知识的理解和掌握,培养了学生的批判意识;让学生内心的“不平衡”通过探究寻找了“平衡”的支点。比如,教学“圆锥的体积”时,我把学生四人一组做实验,要每组的桌上放了大小不一的圆柱与圆锥,学生可以自己选择。我有意识地安排实验工具,有的组是等底等高的圆锥与圆柱;有的组圆锥与圆柱不等底等高;有的组两种都有。小组代表在教具中取实验用的空圆锥圆柱各一个,分头操作。
实验开始后,教室里热闹起来了。有的学生取沙,有的在看沙子的多少,有的在记录,还有的学生之间意见发生了分岐,正在争论……看他们的样子,都极为投入,每个人都在忙碌着。忙不是最终目的,操作是形式,找到答案才是目的,任何形式都是为目的服务的。
实验之后各小组之间出现了不同的实验结果。
“我们将空圆锥装满沙子,然后倒入空圆柱中,三次正好装满,说明圆锥的体积是圆柱的三分之一。”第一组的学生说。
“我们也是三次倒满,圆锥的体积是圆柱的三分之一。”第二组的学生马上接了上来。
“不对,是四分之一,我们倒了,而且每次都看得很准,四次正好装满。说明圆锥的体积是圆柱的四分之一。”第四小组的学生很肯定地说着。
“我们在空圆锥里装满沙子,倒到空圆柱中,不到三次就装满了?”第三小组的学生有点疑惑不解了。
“是三分之一”
“是四分之一” ……
教室里沸腾了,通过动手操作,在实践中学生找到了不同的结果,在相互的交流中碰撞出了思想的火花。
我故意装着不解地说:“到底是几分之几呢?我也想试试!”
我从教具中随手取出一个空圆锥一个空圆柱,举起来说:“你们看, 将空圆锥装满沙子,倒入空圆柱里。一次,再来一次,两次正好装满,圆锥的体积是圆柱的二分之一?”
教室里的声音又大了起来,学生们议论纷纷。
“老师,你取的圆柱太大了。”有个学生看了出来。我在他的推荐下重新使用一个空圆柱继续实验,三次正好倒满。然后学生调换教具,再试,果然都是三次了。
我马上问道:“看来圆锥的体积是圆柱的三分之一,前提条件是什么?”
学生恍然大悟,原来是老师制造了一个小小的错误,故意选用了一个大的圆柱容器。“噢,我明白了,圆柱与圆锥只有在等底等高的情况下,圆锥的体积才是圆柱体积的三分之一。”这次学生真的明白了,欢快地叫了起来,教室里充满了欢笑声。
对于“等底等高”,学生往往会出现错误的理解,教师没有回避或遮掩,而是故意暴露错误,让学生动手操作,在看似“混乱无序”的实践中,增加了学生对实验条件的辨别及信息的批判。学生学得主动,经历了一番观察、分析、发现、合作、创新的过程,既圆满地推导出了圆锥的体积公式,又促进了学生实践能力和批判意识的发展。而这些目标的达成完全是从正确对待实验中的一些“错误”开始的。有时候在教学中设计一些错误,给学生设置一些障碍,让他们走一点弯路,把思考问题的实际过程分析出来,学生对所学的知识理解才会更深,体验才会更真。
二 引出错误,争中反驳
在课堂教学中,学生会出现各种各样的错误,有的老师在学生出现错误时,采取“马上制止”或“立即纠正”的方法,但这样做却忽视了错误的价值。我在教学“三角形内角和”一课时,有意识地进行灵活调控,变错为宝,使课堂变得更加精彩。例如,在探究得出三角形内角和是180°后,学生顺利完成了基础练习,接下来是一道拓展练习题:四边形的内角和是多少度?学生独立思考后,有下面一段课堂对话:
生1:四边形内角和是360°。因为长方形内角都是直角,和是360°。所以我猜想一般四边形内角和是360°。
师:他从特殊到一般,得出四边形内角和是360°的猜想,大家能进一步说明为什么吗?
生2:我在一个四边形里画一条直线(展示她的画法,实际上是一条对角线),把它分成两个三角形,每个三角形内角和都是180°,两个就是360°。
师:大家同意她的意见吗?
学生们表示同意,正当我准备进行课堂小结时,一个学生站了起来,反驳了她的发现。
生3:老师,我不同意刚才生2的意见,我认为她的方法是错的。我用她的方法试了试,在四边形里面画两条这样的线,就分成四个三角形,内角和一共是720°,多了360°。
他的一番反驳,让我犯难了。谁能简单地说她的发现是错的吗?怎样让大家都理解这多在哪里呢?我把问题抛给了学生。
师:这位同学很细心,发现画两条对角线就多出了360°。为什么会多出360°呢?请大家和这位同学一样,在四边形里画出两条对角线,仔细思考,分成的四个三角形内角和与原来四边形的内角和有什么关系?然后小组讨论。
这次意外的缘起是学生画一条对角线,引起错误的“发现”进行反驳,这个错误本身富有研究价值。讨论中同学们发现,多出360°是因为在对角线交点处,新增加了一个周角,周角恰好是360°。而这个周角不属于四边形的内角,在计算四边形内角和时,要减掉这多出来的360°。寻找、思考、交流和反驳的过程,正是学生的空间思维和逻辑思维能力得到发展的过程。这是一个错误,更是一次机会。当时我没有往下进行预设的小结,而是把课堂还给学生,让他们去操作,去分析,去讨论,去反驳,从而把这个错误转化为宝贵的课程资源。
三 将错就错,争中明理
在课堂教学实践中,教者大可不必视学生的“错”为洪水猛兽,只要错的合理,错得其所,教师也不妨试一试“将错就错”,让学生在争论中明理,因为学生在去伪存真、去粗取精的求知过程中,所习得的本领才是真正被他们所内化吸收的本领。比如,我在教学“分数除以分数”之后的一节练习课中,“学校小星星合唱团有团员32人,其中六年级学生占25%,五年级学生占![]() 。合唱团中五、六年级学生各有多少人?
。合唱团中五、六年级学生各有多少人?
大部分学生很快列出了算式:32×25%=8(人);32×![]() =12(人);少部分学生由于受思维定势的干扰,列出了算式:32÷25%=128(人);32÷
=12(人);少部分学生由于受思维定势的干扰,列出了算式:32÷25%=128(人);32÷![]() =85
=85![]() (人)。
(人)。
此时,群起反对,引起了哄堂大笑。我微笑着说:我也觉得少部分同学的解法有道理,那谁能用什么办法说服我们接受你们的观点呢?学生你一言我一语地争论开了:
生1:根据题意,学校小星星合唱团的人数才32人,而第二种解法的计算结果表明,无论五年级合唱团的人数还是六年级合唱团的人数都比全校合唱团的总人数还要多,不符合常理,因此,不用计算就可以知道,第二种解法是不对的。全班学生掌声祝贺。
生2:我再补充一点,如果依据第二种想法,把五、六年级合唱团的人数合并起来,已经有210人左右,比题意中的学校小星星合唱团的人数多出180人左右,太离谱了。还有五年级合唱团人数不是整数,很明显是不对的。
此时,做错的一生自告奋勇地说:噢!明白了,之前是因为我没有认真审题,贸然采取了除法计算。听了大家的争论,通过仔细审题,可以知道,六年级合唱团的人数占全校合唱团人数的25% ,所以,求六年级合唱团的人数就是求全校合唱团人数的25%是多少,也就是求32人的25%是多少,当然用乘法计算,同理可得求五年级合唱团的人数也应该用乘法计算。全班同学响起雷鸣般的掌声。
针对以上的“错解”,我没有急于解释,而是把错误抛还给学生,将错就错,学生则综合运用了估算、联系生活实际、认真审题等解题策略,这对锻炼学生的思维是何等的珍贵;由于我坚定地站在弱势群体这边,既让全班大部分学生在思维碰撞的过程中体验到成功的喜悦,又巧妙地保护了一小部分学生的学习积极性,可谓一箭双雕;采取了“将错就错”的策略,巧妙地创造了一个民主、平等的教学场,使学生敢想、敢说、敢做,思维被彻底激活了。
四 善待错误,争中内化
记得有人说过:“教室——学生出错的地方”。错误是伴随着学生一起成长的。善待学生的“出错”,课堂能够得到有效生成,也能在争论中内化知识。比如,我在教学《平行四边形面积公式的推导》一课时,请学生们拿出事先准备好的平行四边行的框架来玩一玩,启发学生从中发现。学生们一边使这个框架不断地变大、变小,一边在积极地思考着,相互地商量着。终于,一位学生带着探究后发现的兴奋走上讲台,俨然是一个“小老师”的模样用一个框架边演示边讲解:我把长方形(如图1)稍稍一拉成平行四边形(如图2)后,问同学:“你们知道现在平行四边形的面积是多少吗?为什么?”
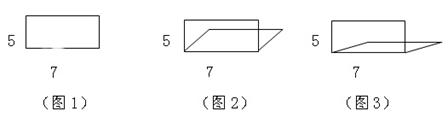
让我始料未及的是几乎全班都是“7×5=35”,这位“小老师”还慷慨陈词了----因为两条邻边还是7和5,没变!无疑,已有的“长方形面积计算”的认知基础局限了孩子们的视野, 这的确就是孩子们的看起来似乎有些糟糕的“思维实际”,不过从中我们不也正能窥见孩子们数学建模的一面吗?孩子们潜意识里已试图运用已有的“邻边相乘”旧知识解决新问题了呀,不正说明“转化”的数学思想已深入孩子们的小心灵了吗?课得白銀继续啊!----“怎么办?”真是急中生智:我一声不吭,继续请“小老师”演示,只见“小老师”微笑着一拉、再拉,拉至几乎上下邻边挨近时(如图3)我故意提高嗓门问:“那照你们的想法一定还是五七三十五喽?”孩子们或搔头挠耳或面面相觑,还窃窃私语----他们相邻的两条边的长度不变,乘积也应该不变,但是这个平行四边行明显地越来越小了,也就是面积变了,所以平行四边行的面积的计算不能用相邻的两条边的乘积!教室里充满了欢笑声。
学生错误“错”得顺其自然,在面对这个真实的错误后,老师没有回避,也不是等待,而是善待错误,顺水推舟,让学生不断的拉着那框架,在思考、争论、实践中内化知识,这就是“错误”带来的附加值。课堂生活本身就是丰富多彩的,“偏差”、“失误”也必然是其中的一部分,当我们追求课堂的真实自然,敢于暴露学生的“错误”时,“节外生枝”的不顺反而会给课堂注入新的生命力,茅塞顿开、豁然开朗一定是孩子们的共同兴奋点,课堂更是呈现出风回路转、柳暗花明的神采!
错误是正确的先导,是通向成功的阶梯,有时更是创新火花的闪现。教师在教学中要善于把握机会,要创造性地对待学生的“错误”,让学生从错误中获得更多更完美的知识。学生的“错误”是宝贵的,课堂正是因为有了“错误”才变得更加精彩;因为有了“错误”,课堂才生机和活力;因为有了“错误”,师生才更具灵性和个性。“宁要真实的缺憾,不要虚假的完美”将是我一生教学中不变的追求。最终,让错误成为数学课堂教学的一个亮点,为数学教学添上一道亮丽的风景线。
参考文献:
1、《数学课程标准解读》
2、《小学青年教师》
3、《小学数学教育》