概念是人们对事物本质的认识,是逻辑思维的基本单元和形式。人类对外部世界的正确认识,是在概念的不断形成、发展与完善中,在旧的概念向新的概念不断重组、转化和更新中实现的。所以,概念的变化与发展,反映了人类认识世界的进步和发展。
在数学学习活动中,学生从生动的直观到抽象的思维,形成一系列数学概念,这些数学概念的真理性又返回数学实践中接受检验。在这个过程中,数学概念经过了不断的发展与变化,正是这种概念的发展与变化,使学生的认知不断地实现“同化”与“顺应”,认知结构不断重组、优化,学生的思维得到进步和发展。
在数学教学中,教师要正确把握概念表现出的不同方面,充分展现概念的形成过程,从而帮助学生真正地理解概念。
一、动手操作中层现概念形成过程,帮助学生自主建构概念。
学生数学学习的过程是一个建立在经验基础上的主动建构的过程,而且小学生的思维处在具体运演阶段,其对于概念的理解是建立在直观形象的基础之上的,所以在数学概念教学中,教师必须给学生充分动手操作的机会,在动手操作中展现概念的形成过程,让学生亲身经历数学概念形成过程中形象而生动的性质,充分展现概念发生、发展、形成的过程;让学生充分经历“个性化”的定义过程,以便使学生对概念的自主建构和真正理解成为可能。
例如长方体的长、宽、高的概念的形成过程。
首先,学生动手操作,利用小棒和橡皮泥制作一个长方体,其棱(小棒)和顶点(橡皮泥)一目了然。
其次,引导学生思考:如果我们拿掉其中的一根小棒,还能看出这个长方体的大小吗?学生拿掉其中一根小棒后发现,根据剩下的11条棱,我们仍然能够看出长方体的 大小。
再次,引导学生思考:最多可以拿走多少根小棒,最少剩下哪几根小棒,我们仍然可以看出长方体的大小?让学生想一想,试一试。
最后,学生通过动手实践后发现,最多拿走9根小棒,剩下相交于同一个顶点的3 根小棒后,仍然可以确保我们看出一个长方体的大小。
这样,长方体的长、宽、高的概念便水到渠成地得出。此时概念的获得过程是学生自主建构概念的活动过程,原本抽象的数学概念在学生的动手实践中得以自主建构,概念的形成更加外显,概念的获得更加鲜活,概念的抽象变得形象,概念的理解更加深刻。
二、反面例证中层现概念形成过程,帮助学生全面认识概念。
没有比较就没有鉴别。一个数学概念在学生头脑中初步形成之后,如果缺少相应的变式”的理解,将会是模糊的、不全面的。只有通过正面的强化理解与反面的对比认识的互相沟通,让学生的思维经历从“立”到“破而后立”的螺旋式上升的认识过程,才能真正帮助学生建立起对数学概念的深刻理解。同时帮助学生在理解概念的基础上,进一步沟通核心概念及其相关概念的联系,起到举一反三、触类旁通的学习效果。
例如三角形的概念的形成过程。
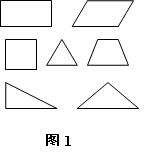
首先,让学生准备好各种平面图形卡片(如图1),引导学生思考:将所有这些图形分成几类,你会怎么分?为什么?学生能够容易地得到:可以将三角形单独分为一类,因为它们都是有三条线段的图形。
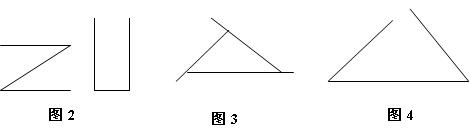
其次,针对“三条线段”的图形,我们可以出示反例(如图2):这两个图形也是由三条线段组成的,它们是三角形吗?为什么?学生意识到,三角形不仅仅是由三条线段组成,而且是由三条线段围成的。
再次,针对“三条线段围成”,我们进一步出示反例(如图3):像这样,由三条线段围成的图形是三角形吗?很显然,这时的三条线段没有首尾相连,因而组成的图形不是三角形。
最后,为了强调“首尾相连”,我们可以继续出示反例(如图4):像这样,你认为它们是不是符合首尾相连的要求,是三角形吗?这时,学生会认识到,三条线段没有全部首尾相连,还有一个缺口,没有封闭。
通过反例,激起学生认知冲突,促使学生在层层递进的矛盾解决中建立起数学概念,丰富对数学概念的理解,形成对数学概念全面、深刻的理解。
三、概念限制中层现概念形成过程,帮助学生逐步抽象概念。
我们可以通过概念的限制,把一个外延较大而内涵小的概念逐步丰富变化为一个外延小而内涵丰富的新的概念。概念的限制过程就是一个强抽象的过程,它立足于已有概念,引入新的特征或条件得到新的概念,使新的概念成为原概念的一个特例。概念的限制过程既展示了概念的逐步抽象过程,又向学生渗透了获取知识的方法。
如“因数”、“公因数”、“最大公因数”等概念的认识过程。
从学生的认知规律和知识的逻辑体系考虑,我们首先学习了“因数”的概念,此时学生能够求出一个数的因数。在此基础上,我们就可以求出两个或更多数的因数,其中它们共有的因数即为“公因数”。这时的“公因数”的概念就是利用概念的限制,缩小了“因数”概念的外延得到的一个新的概念。同理,我们继续缩小“公因数”概念的外延,将“公因数”限制在“最大”的条件内,得到“最大公因数”的概念。
因为概念的限制过程注重将未知转化为已知,由已知得到未知,立足原有知识经验基础,所以,利用概念的限制来获得和认识新的概念,知识发展脉络会更顺畅,认识过程会更符合学生学习的心理特点和认知规律。
四、类比推理中层现概念形成过程,帮助学生形象理解概念。
类比推理是根据两个对象具有某些相同的属性,其中有一个对象还有另外某个属性,从而推论出另一个对象也可能具有这个属性。它是一种根据事物的相同点,从已知到未知,探求新知识的方法,非常便于学生发现、理解和生成新的数学概念,扩大认识成果,启发学生认知。
例如在教学“梯形”概念时,“只有一组对边”和“一组对边”有何不同,学生理解起来十分困难。如何帮助学生理解呢?
首先,引导学生比较“老师会用筷子吃饭”和“老师只会用筷子吃饭”这两个句子有什么不同?学生认识到,“会用筷子吃饭”就是说老师除了会用筷子吃饭外,还能够用其他的东西吃饭,比如勺子、叉子等等,而“只会用筷子吃饭”就是说老师除了筷子,就不会用其他的东西吃饭。这样,学生在熟悉的生活情境中,理解了“有……”和“只有……”的区别。
其次,理解“梯形”的概念,并把它与“平行四边形”的概念进行对比。有了前面的铺垫,学生认识到,梯形和平行四边形都有两组对边,但是平行四边形的两组对边都要平行,而梯形的两组对边中,只有一组对边平行,另一组对边不平行。另有学生补充,如果不强调“只有一组”的话,那两组对边平行时我们也可以说其中有一组对边平行。这样,学生对于梯形的概念有了更明确的认识。
为了认识和解释某些数学概念,我们往往可以找出另一种和它相似的事实或原理,然后通过类比推理进行说明。类比推理可以把未知的变成已知的、深奥的变成浅显的,这有利于学生根据数学概念之间的相似点去认识新的数学概念,有利于启发学生思维,起到举一反三、触类旁通的学习效果.