一.教学任务分析
学生学习平面解析几何后,对运动对象的不变性有了一定的了解。本课的教学任务是让学生通过对满足一定条件的动直线的不变性(如恒过某定点)的探究,了解“囿变几何对象的不变性”探究的基本方法,这是解析几何中的常见问题,也是学生数学学习的一个难点。这类问题之所以成为学生学习的难点,主要是所研究的几何对象动不起来。为此,我们利用TI图形计算器这一平台可以解决这一困难. 本节课的主要教学目的是训练学生从特殊到一般的归纳能力,以及从运动变化的事物中寻求“规律”的能力. 学生这些能力的形成,会使他们即使有一天忘记了曾学习过的某些具体问题,但是研究这些问题的思想与方法却已深深地烙在他们的脑海中了。
二.教学重点难点
重点:训练学生从特殊到一般的归纳能力,以及囿变几何对象的不变性的探究方法。
难点:在获得囿变几何对象的不变性后,如何从数学上加以严格的证明.
三.教学基本流程

四.教学情景设计
|
问 题 |
问题设计意图 |
师生活动 | |
|
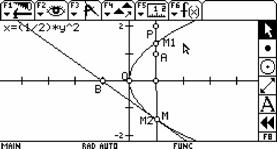
1.已知抛物线 |
在运动中发现结论:动直线恒过某定点. |
师:让学生动手操作,或老师在屏幕演示
| |
|
略解:设 由 将 另一方面,设直线 | |||
|
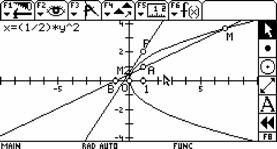
2.如果点 |
发现新的问题 |
生:猜想结果,观察动画,发现规律,验证猜想. | |
|
结论:不论点 | |||
|
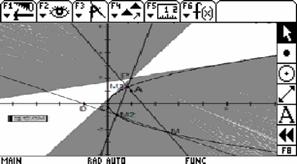
3.已知点 |
进一步研究较为复杂的动直线恒过定点的问题. |
生:通过观察,发现定点的大概位置,并形成解题思路 | |
|
略解:设
与抛物线方程
同样的方法可求得 设直线 与抛物线方程
即 按字母 由 | |||
|
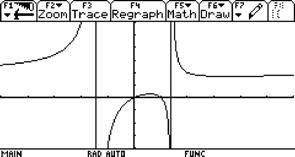
4.思考一系列的问题 (1)当 (2)当 (3)当M、A、B三点共线时情况如何? |
多方面观察,培养思维的严密性,在技术环境下让思维能力得到更充分的发挥. |
师生:(1)当点 如下图. | |
|
| |||
|
5.求直线 (这个问题是由追踪直线 |
培养逆向思维的能力和数形结合的数学思想方法. |
| |
|
略解:这是一个利用导数求函数的值域的问题.前面我们已经求出 |
| |
|
6.能否从知识、方法、技术三个方面对本节课进行小结? |
学会概括总结,加深对知识和方法的理解掌握. |
师:从三个方面让学生回顾本节课所学内容. 生:讨论、提炼、语言刻画. |
五.课后反思
信息技术的介入使我们的学习方式发生了根本性的改变,并且使我们的数学思维形式发生了变化。在技术落后的时候,我们把大部分精力都花在复杂的计算和凭空的伦铜想象中。虽然运算能力和想象能力是数学的重要能力,但是人的计算能力和想象的空间毕竟是有限的。有了技术的介入,我们的运算和想象力就象插上了翅膀,我们不再为生活中的大量繁琐的数据而犯愁,我们也不再满足于只会做一两个题目。
本文获得“高中数学课程教材与信息技术整合的研究”课题子课题论文和优秀案例评比一等奖
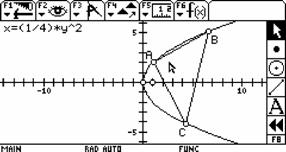 生:发现不变的点
生:发现不变的点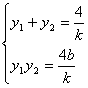
 直线
直线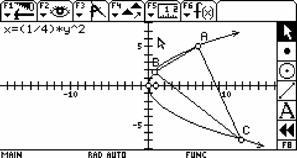 师:演示课件,或让学生自己动手.
师:演示课件,或让学生自己动手.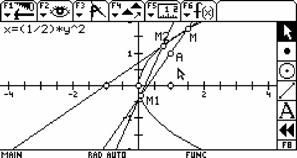 师:演示课件,或让学生自己动手.
师:演示课件,或让学生自己动手.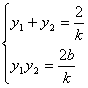 。将①②分别代入并解之得
。将①②分别代入并解之得
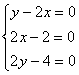 解得
解得