为了和国际数学接轨,全日制普通高级中学教科书中增加了向量的内容,随着课程改革的进行,向量的应用将会更加广泛,这在2004年高考数学试题中得到了充分的体现。向量在研究空间几何问题中为学生提供了新的视角,但在教学中,我们的应用还不够,特别是法向量的应用,教科书中只给了一个概念:如果非零向量![]() ,那么
,那么 ![]() 叫做平面
叫做平面![]() 的法向量,实质上,法向量的灵活应用,将使得原本很繁琐的推理,变得思路清晰且规范。本文将介绍法向量在空间几何证明、计算中的应用。
的法向量,实质上,法向量的灵活应用,将使得原本很繁琐的推理,变得思路清晰且规范。本文将介绍法向量在空间几何证明、计算中的应用。
(一)直线 ![]() 的方向向量和平面
的方向向量和平面![]() 的法向量分别为
的法向量分别为 ![]() ,则直线
,则直线 ![]() 和平面
和平面![]() 所成的角
所成的角 ![]() 等于向量
等于向量![]() 所成的锐角(若所成的角为钝角,则为其补角)的余角,即
所成的锐角(若所成的角为钝角,则为其补角)的余角,即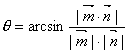 。
。
(2003全国(理)18题) 如图,直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,![]() ,侧棱
,侧棱![]() ,
,![]() 分别是
分别是![]() 与
与![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 上的射影是
上的射影是![]() 的重心
的重心![]() ,
,
(Ⅰ)求![]() 与平面
与平面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(Ⅱ)求点![]() 到平面
到平面![]() 的距离。
的距离。
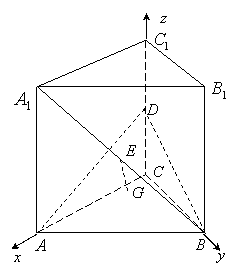
(Ⅰ)解:以![]() 为坐标原点,建立如图所示的坐标系
为坐标原点,建立如图所示的坐标系![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,
由 ![]() 得,
得,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,![]() ,由
,由![]() ,
,![]() 得,
得,
![]() ,令
,令![]() 得,
得,![]() ,
,
∴平面 ![]() 的一个法向量为
的一个法向量为![]() ,
,
∴ ![]() 与
与![]() 的夹角
的夹角![]() 的余弦值是
的余弦值是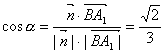 ,
,
∴ ![]() 与平面
与平面![]() 所成角为
所成角为![]() 。
。
当直线与平面平行时,直线与平面所成的角为![]() ,此时直线的方向向量与平面的法向量垂直,我们可利用这一特征来证明直线与平面平行。
,此时直线的方向向量与平面的法向量垂直,我们可利用这一特征来证明直线与平面平行。
(二)如果不在平面内一条直线与平面的一个法向量垂直,那么这条直线和这个平面平行。
(2004年高考湖南(理)19题)如图,在底面是菱形的![]() 四棱锥中,
四棱锥中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,
,
(I)证明:![]() ;
;
(II)求以![]() 为棱,
为棱, ![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小;
的大小;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?证明你的结论。
?证明你的结论。
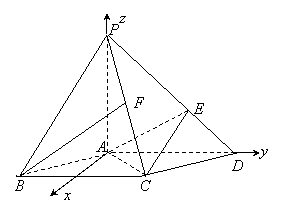
(Ⅲ)解:以![]() 为坐标原点,直线
为坐标原点,直线![]() 分别为
分别为![]() 轴、
轴、![]() 轴,过
轴,过![]() 点垂直平面
点垂直平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系(如图),由题设条件,相关各点的坐标分别为
轴,建立空间直角坐标系(如图),由题设条件,相关各点的坐标分别为![]() ,
, ![]() ,
,
∴ ![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则由题意可知,
,则由题意可知,![]() ,
,
由![]() 得
得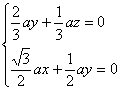 ,
,
∴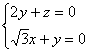 令
令![]() 得,
得,![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为![]()
设点![]() 是棱
是棱![]() 上的点,
上的点,![]() ,则
,则
![]() ,
,
![]()
由 ![]() 得,
得,![]()
∴ ![]() , ∴当
, ∴当![]() 是棱
是棱![]() 的中点时,
的中点时,![]() 。
。
同样,当直线与平面垂直时,直线与平面所成的角为![]() ,此时直线的方向向量与平面的法向量平行,我们可利用这一特征来证明直线与平面垂直。
,此时直线的方向向量与平面的法向量平行,我们可利用这一特征来证明直线与平面垂直。
(三)设二面角![]() 的两个半平面
的两个半平面![]() 和
和![]() 的法向量分别为
的法向量分别为![]() ,设二面角
,设二面角![]() 的大小为
的大小为![]() ,则二面角的平面角与两法向量所成的角相等或互补,当二面角的锐角时,
,则二面角的平面角与两法向量所成的角相等或互补,当二面角的锐角时,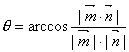 ;当二面角为钝角时,
;当二面角为钝角时,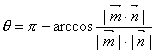 。
。
我们再来看2004年高考湖南(理)19题:
(Ⅱ)解:由题意可知,![]() ,
, ![]() ,
,
∵ ![]() ∴
∴ ![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,则由题意可知,
,则由题意可知,![]() ,
,
由![]() 得
得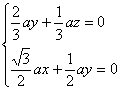 ,
,
∴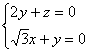 令
令![]() 得,
得, ![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴向量![]() 与
与![]() 夹角
夹角![]() 的余弦值是
的余弦值是 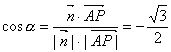 , ∴
, ∴ ![]() ,
,
由题意可知,以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角
为面的二面角![]() 是锐角,
是锐角,
∴所求二面角的大小为![]() 。
。
我们知道当两个平面的法向量互相垂直时,两个平面所成的二面角为直角,此时两个平面垂直,我们可用这一特征来证明两个平面垂直。
(四)设两个平面![]() 和
和![]() 的法向量分别为
的法向量分别为![]() ,若
,若![]() ,则这两个平面垂直。
,则这两个平面垂直。
(1996年全国(文)23题)在正三棱柱![]() 中,
中,![]() ,
, ![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() 。
。
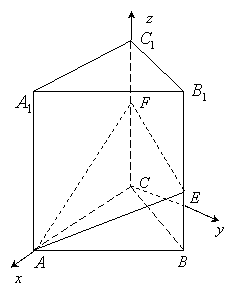
证明:以![]() 为坐标原点,建立如图所示的坐标系
为坐标原点,建立如图所示的坐标系![]() ,
,
则 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则由题意可知,
,则由题意可知,![]() ,
,
由 ![]() 得
得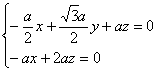 ,
,
∴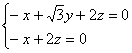 令
令![]() 得,
得,![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由题意可知,平面![]() 的一个法向量为
的一个法向量为![]()
∴ ![]() ∴平面
∴平面![]() 平面
平面![]()
(五)设平面![]() 的法向量为
的法向量为![]() ,
,![]() 是平面
是平面![]() 外一点,
外一点, ![]() 是平面
是平面![]() 内一点,则点
内一点,则点![]() 到平面
到平面![]() 的距离
的距离![]() 等于
等于![]() 在法向量
在法向量![]() 上的投影的绝对值,即
上的投影的绝对值,即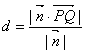 。
。
我们再来看2003年全国(理)18题:
(Ⅱ)解:设 ![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,
设平面 ![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,![]() ,
,
由![]() ,
,![]() 得,
得,
![]() ,令
,令 ![]() 得,
得,![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为![]() ,而
,而![]() ,
,
∴点![]() 到平面
到平面![]() 的距离
的距离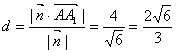 。
。
我们知道直线与平面、两个平面的距离都归结为点到平面的距离,故此法同样可以解决直线与平面、两个平行平面的距离。
(六)设向量![]() 与两异面直线
与两异面直线![]() 都垂直(我们也把向量
都垂直(我们也把向量![]() 称为两异面直线
称为两异面直线![]() 的法向量),
的法向量),![]() 分别为异面直线
分别为异面直线![]() 上的点,则两异面直线
上的点,则两异面直线![]() 的距离
的距离![]() 等于
等于![]() 法向量
法向量![]() 上的投影的绝对值,即
上的投影的绝对值,即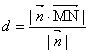 。
。
(1999年全国(理)21题)如图,已知正四棱柱![]() 中,点
中,点![]() 在棱
在棱![]() 上,截面
上,截面![]() ,且面
,且面![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]() 之间的距离。
之间的距离。

解:以![]() 为坐标原点,建立如图所示的坐标系
为坐标原点,建立如图所示的坐标系![]() ,
,
连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() 就是
就是
面 ![]() 与底面
与底面![]() 所成的角的平面角,
所成的角的平面角,
∴![]() =
=![]() ,∴
,∴![]()
又∵截面![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴ ![]() 为
为![]() 的中点,∴
的中点,∴ ![]() ,
,
则 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,![]()
设向量![]() 与两异面直线
与两异面直线![]() 都垂直,由
都垂直,由 ![]() ,
,![]() 得,
得,
∴![]() ,∴
,∴ ![]() ,
,
∴异面直线![]() 与
与![]() 之间的距离
之间的距离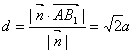
前面介绍了利用法向量解决空间几何的证明与计算问题,实现了几何问题的代数化,将复杂的几何证明转化为代数运算,从而避免了几何作图,减少了逻辑推理,降低了难度。但公式的应用也有一定的局限性,一般地,在能建立空间直角坐标系的情况下,利用法向量较为有效。