在数学学习中，不少同学遇到了这样的情况：每个新学的知识点都懂，后面的习题也会做，但到了一章学完以后，不仅综合性的题不会做，甚至连做过的习题也不会做了．对这一现象的解释，一般认为是由于知识遗忘、综合运用能力不高而造成的正常现象，不必为此惊慌．事实真的是如此吗？
其实，正常现象之说是站不住脚的，根本原因在于平时的学习中出了问题．学习新课时，许多同学只是机械地把基础知识记住，跟着课本的思想搞懂例题的每个步骤．至于．后面的同步习题，用这些知识一套就灵，仿照例题去做准行．看起来似乎学得轻松，其实在不知不觉中忽视了不少重要的方面．例如，公式的发现和推导过程，与前面所学知识的联系，所涉及的数学思想方法等等．
由于教材上每节后面的习题与知识点同步，因此多数题能用本节知识对号人座地解出，从而掩盖了学习中存在的许多问题．这种现象，笔者称之为“新课效应”．它是学习数学的大敌，严重影响了综合运用能力的提高，尤其是对高中阶段的学习危害更大．如何才能克服新课效应呢？
一、学习新知识时不仅要且税结论，而且要重视过程
数学上的每一个知识点都不是孤立的，从问题的提出到最后解决，要用到大量已学知识和一些很重要的数学思想方法．所以，在这个过程中可以复习已学的许多知识，初步认识和后面知识间的联系，在头脑中形成知识网络的雏形，在这个过程中也要重视学习教学思想方法．如：对数的运用法则的证明过程，就涉及到幂的运算法则、对数的定义、对数式与指数式的互化等知识．其证明方法是设出式子的值，再进行等式变形，这是数学上一种很有效的思想方法．再如，直线平面垂直的判定定理的证明过程，先证特殊情况，再把一般情况归结为已证的情况，使本来复杂的问题简化了许多．这里用了数学上非常重要的分类讨论思想和化归思想．
二、学习中要随时注意归纳
归纳在学习中有神奇的作用．通过归纳，可以使人透过现象看本质，找到知识的精华；通过归纳，可以使所学知识条理清晰，用起来得心应手；通过归纳，可以找到致错根源，避免再犯同样的错误．那么，应该如何归纳呢？
1．归纳知识中存在的规律例如，对数函数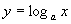
的性质3：
| a>1 | 0<a<1 | |
| x>1 | y>0 | y<0 |
| 0<x<1 | y<0 | y>0 |
表中有四种情况，有的同学总是记错或记不住．其实，它们有以下规律：a和x同时在区间（0，1）或者（1，＋co）内取值时
＞0；a和x分别在区间（0，l）和（1，＋co）内取值时，
＜0，简化为“同区间得正，异区间得负”．这样，不但容易记，而且运用也很方便．只要留心，规律是可以发现的．
2．归纳每部分知识，认识知识体系和网络 如《立体几何》第一章“空间直线和平面”这部分，先找出直线和平面的三种位置关系，再沿平行和相交这两条线索往下讨论．这样，就可以把这部分知识的结构理清楚，使头脑中的知识成为一个有条不紊的网络．
3 ．归纳题型和思想方法 见多识广肯定能提高运用知识的能力．但是，若对见过的东西不加以归纳，恐怕很难领会其精髓．如，求定义域的题很多，但真正算起来却只有含分母、偶次根式、对数、三角和反三角函数、实际问题中的函数这些主要情况．高一教材中出现得较多的思想方法有分类讨论、换元、数形结合、化归、特殊化等．
三、波动式学习
学习知识应像滚雪球一样不断累积。为了做到这一点，加强复习和归纳是非常有效的做法，此外，还应注意以下三点：
1. 一题多解 如前所述，教材上的多数习题都能用该节知识对号入座地解出。若能再找出一些解法，就能更多地用到以前学过的知识，达到前后联系，使新旧知识融合的目的。
2. 解题时放开思路 有的同学习惯于做哪一节的习题就拿该节的知识去套，完全不考虑别的方法，这是非常有害的。正确的学习方法是不给自己的思维画框框，读懂题后尽可能去联想学过的所有知识，从中选出最佳解题方案。
3. 适当补充一些带综合性的练习题 可从课外读物中选一些较好的题来做。当然，有经验的老师也会随时补充一些好的题目。
以上，笔者谈了“新课效应”的形成原因及克服它的方法，希望对同学们克服“学时全懂，学完后全不懂”这一怪现象有所帮助。