例谈创造性思维的自我培养

下面具体谈谈数学学习中，创造性数学思维如何自我培养，供同学们参考．

1.培养发散思维

在数学教学中，通常是教师按照教材固有的知识结构，按照单向思维方式从题目的条件和结论出发联想到已知的公理、定理、公式和性质，只从某一方向思考问题，采用某一方法解决问题，应该说这种方式是解决问题的基本方法，但是长期按照这种方式去思考问题就会形成“思维定势”，严重制约了同学们的创造性思维．因此同学们在数学学习中要逐步养成用发散性思维去思考问题，经常运用一题多思、一题多解、一题多变等思索方法，显得十分重要．

 例如，已知a+b=l，a＞0，b＞0，求的最小值．根据题目的结构特征，可以从三角、数列、不等式、方程、函数、几何以及常数更换等各种背景下进行一题多思，从而一题多解，而且通过比较，寻求最佳解法，例（常数更换）可能是解决此类题的最佳方法；还可进一步通过改变或调换题设和结论以及将条件和结论拓广进行一题多变训练，例如本题可拓广出：已知（P，Q，R为正常数），且 a＞0，b＞0，c＞0,求ma+nb+c（m，n，为正常数）的最小值．通过训练，同学们可以尝试到用发散思维方法从多个方面思考问题的全新感觉，加深了对知识的理解，提高了思维能力．

2.善用逆向思维

正向思维是从题给的已知条件出发，按条件的先后顺序，按常规的思路去研究某一数学问题，而逆向思维就是倒过来想问题．解题过程中适时利用逆向思维逐渐培养自己的独立思考能力，确实可独辟溪径，突破难点，化繁为简．

例如，若函数 y=f(x)的图象上的每一点的纵坐标不变，横坐标伸长到原来的2倍，然后再将整个图象沿x轴向左平移个单位，沿y轴向下平移1个单位后所得图象与的图象相同，求f(x)的表达式．本题若按常规思维，应设f(x)的解析式，显然较繁．同学们不妨逆向解题，一则可以培养逆向思维能力，二则解题过程简单明了．具体过程如下：

3.构建整体思维

整体思维是整体原理在数学中的反映．在数学解题中，同学们的思维不一定要集中在问题的个别部分，有时要将问题看作一个整体，通过研究问题的整体形式、整体结构或作种种整体处理后，达到顺利而又简捷地解决问题的目的．

例如，求sinl0°sin30°sin50°sin70°的值．若将整个乘积看成一个整体，可得如下解法：设a=sinl0°sin30°sin50°sin70°，b=cosl0°cos30°cos50°cos70°两式相乘然后运用倍角公式后可解得。当然，若把a转化成：cos80°cos60°cos40°cos20°，则通过对上式整体结构的解剖后，可由“连锁反应”即通过分子、分母都乘以8sin20°多次运用倍角公式来解，显得更为简洁！

又如 2000年高考13题：一个长方体共一个顶点的三个面的面积分别是，这个长方体对角线的长是（A）（B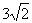） （C） 6 （D）整体考虑的关系（）和长方体的各面面积又是三度中任二度相乘，很容易猜出三度分别为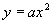，故答案为（D）．

4．注意直觉思维

当人们解一道数学题时，往往要对结果或解题途径先作大致的估计（估量）或猜测，这就是一种直觉（思维）．在解决抽象的数学问题时，要时刻注意利用直觉思维解题，以培养自己能把抽象转化为具体（形象）的能力．值得指出的是，能把抽象转化为具体，本身也是一种抽象思维能力．

例如 2000年高考第 11题：过抛物线（a>0)的焦点心F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别为p、q，则等于(A)2a (B) (C) 4a (D) 。

分析1： 首先抛物线方程化成标准形式为，其次当PQ为通径时可求得，由此可知，本题答案为(C)。分析2：当直线PQ的斜率趋向于 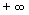时，其中一条（不妨设PF）的长度趋向于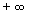，而另一条趋向于OF，从而可求得答案(C)，十分简单。

总之，思维是解题的基础，而思维的灵魂在于它的独立性和创造性。学习数学不只是掌握现成的公式、定理，更重要的是掌握科学的思维方法，培养创造性思维能力对于提高自身素质，从而把自己培养成有用的人才，无疑是十分重要的。