提要 笔者设计了一个数学实验──由学生利用Ti-92图形计算器作二次函数图象,通过 观察、总结在给定的闭区间上,函数的单调性与函数取最值时自变量的取值的关系,寻找二次函数在闭区间上的最值问题的解决方法.由此攻破了教学中的一个重点、也是难点的内容,在此基础上探究另一些函数在闭区间上的最值问题的解决方法.同时看到现代教育技术手段的应用,为打破传统的教学模式(教师讲学生听)开辟了宽敞的道路.
主题词 Ti-92图形计算器 作函数图象 单调性
一、实验背景:
高一学生在初中已学过二次函数,知道二次函数在x可取任意实数时在顶点处取得最大值或最小值,但定义域是闭区间时,二次函数在顶点处还取得最大值或最小值吗?所以笔者设计了一个实验,利用Ti-92图形计算器作函数图象,寻找二次函数在闭区间上的最值问题的解决方法.
二、实验目的:
通过观察函数图象的单调性与最值点的关系,寻找二次函数在闭区间上的最值问题的解决方法;在此基础上探究另一些函数在闭区间上的最值问题的解决方法.
三、实验工具: Ti-92图形计算器
四、实验预习题:(1)试求函数y=2x2-4x-1的最值.(配方法)
(2)试求函数y=x+![]() 及y=x-
及y=x-![]() 的最值.(判别式法)
的最值.(判别式法)
五、实验步骤:
(一)先利用Ti-92图形计算器作出系数为整数的二次函数,y=2x2-4x-1给定区间x![]() [-1,1/2]、[2,3]、[-1,2],分别通过F5中Minimum,Maximum计算出结果.观察函数图象的单调性与图中所示的最值点的位置的关系.
[-1,1/2]、[2,3]、[-1,2],分别通过F5中Minimum,Maximum计算出结果.观察函数图象的单调性与图中所示的最值点的位置的关系.
(二)再改变二次函数,如y=2x2-4x-1及给定闭区间, x ![]() [-3,-2], [-1,1], [-2,1](闭区间要求分别在对称轴左、右侧及相应开区间包括对称轴),重复步骤(1).
[-3,-2], [-1,1], [-2,1](闭区间要求分别在对称轴左、右侧及相应开区间包括对称轴),重复步骤(1).
(三)自行重新设置新函数,(二次函数的系数可为分数且二次项系数正、负均应有),重复步骤(1).猜想解决方法.
(四)实验现象记录:
1、在下面绘制出函数的图象.
函数y=2x2-4x-1, x![]() [-1,1/2] 的图象
[-1,1/2] 的图象
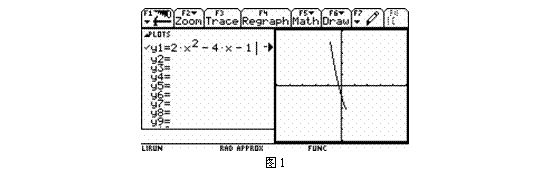
函数y=2x2-4x-1, x![]() [2, 3] 的图象
[2, 3] 的图象
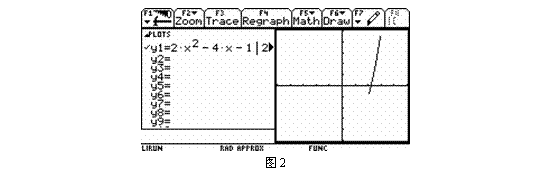
函数y=2x2-4x-1, x![]() [-1 ,2] 的图象
[-1 ,2] 的图象
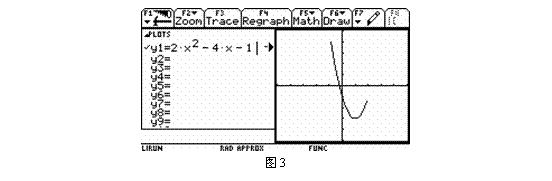
2、完成下表:分别记录函数图象的单调区间与图中所示的最值点的位置(x的取值).
二次函数
|
序号 |
函数 |
定义域 |
单调区间 |
最值点位置(x的取值) 最大值 最小值 | ||
|
递增 |
递减 | |||||
|
1 |
y=2x2-4x-1 |
x |
|
[-1,1/2] |
x= -1 |
x=1/2 |
|
x |
[2 , 3 ] |
|
x=3 |
x=2 | ||
|
x |
[1 ,2 ] |
[-1 ,1 ] |
x= -1 |
x=1 | ||
|
2 |
y=2x2-4x+1 |
x |
[-3 ,-2] |
|
x= -2 |
x= -3 |
|
x |
|
[-1,1] |
x= -1 |
x=1 | ||
|
x |
[-2 ,-1] |
[-1,1] |
x= -1 |
x=1 | ||
|
3 |
|
|
|
|
| |
|
4 |
|
|
|
|
| |
|
5 |
|
|
|
|
| |
|
6 |
|
|
|
|
| |
|
7 |
|
|
|
|
| |
六、实验结论:
(一)通过对以上函数的观察分析,你认为二次函数在闭区间上的最值问题有何规律?
(一个二次函数在闭区间上必有最大值和最小值.解决二次函数在闭区间上的最值问题.可通过闭区间的端点的函数值与顶点的函数值比较大小得出.当定义域分别在对称轴左、右侧,或闭区间的一个端点在对称轴上时,闭区间的端点的函数值为最大或最小值;当顶点的横坐标属于闭区间去掉两端点得到的开区间时,二次函数在顶点及距离顶点较远的闭区间的一个端点处的函数值为最大或最小值.)
(二)数学证明(利用函数图象的单调性可证.)
设函数f (x) = ax2+bx+c (a>0), x![]() [m, n] 则对称轴为x= -
[m, n] 则对称轴为x= - ![]() , 最值分情况
, 最值分情况
讨论:
[1] 当m ≥- ![]() 时,对称轴在区间左侧,f (x)在[m ,n]上递增,则f (x)的最大值为f (n), 最小值为f (m);
时,对称轴在区间左侧,f (x)在[m ,n]上递增,则f (x)的最大值为f (n), 最小值为f (m);
[2] 当n≤-![]() 时,对称轴在区间右侧,f (x) 在[m ,n]上递减,,则f (x)的最大值为f (m),最小值为f(n);
时,对称轴在区间右侧,f (x) 在[m ,n]上递减,,则f (x)的最大值为f (m),最小值为f(n);
[3] 当 - ![]()
![]() (m, n)时,则f (x)的最小值为f (-
(m, n)时,则f (x)的最小值为f (- ![]() );在[m , -
);在[m , - ![]() ]上函数f (x)递减,则f (x)的最大值为f (m),在[-
]上函数f (x)递减,则f (x)的最大值为f (m),在[- ![]() , n]上函数f (x)递增,则f (x)的最大值为f (n),比较f (m)与f (n)的大小即得.
, n]上函数f (x)递增,则f (x)的最大值为f (n),比较f (m)与f (n)的大小即得.
七、拓展:
1、某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的200天内,西红柿市场售价与上市时间的函数关系式为:f (t) =300-t: 西红柿的种植成本与上市时间的函数关系式为:g (t) = ![]() ( t-150)2+100,认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(2000年全国高考题)(转化为二次函数在闭区间上的最值问题)
( t-150)2+100,认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(2000年全国高考题)(转化为二次函数在闭区间上的最值问题)
2、求以下函数在给定区间的最值.
(1)若函数y = x2+x+a在[-1,2]上的最大值与最小值之和为6,则a =----.
(2)求函数y = -x2+tx-1 (t>0), x [-1,2]的最值.(与实验结论的数学证明方法相同)
(3)求函数y = - x2-2x-1, x [t, t+1]的最小值g (t).
(分析:这里函数解析式已定,但是在一个含有参数的闭区间上考察最小值,就要结合区间与对称轴的相对位置进行定位讨论.)
解:f (x) =- x2-2x-1 对称轴x=1
当x=1 ![]() [t, t+1]时,即0≤t≤1时,g(t)=-2;
[t, t+1]时,即0≤t≤1时,g(t)=-2;
当x=1<t时, 对称轴在区间左侧, f (x)在[t, t+1]上递增, g (t)= f (t) =t2-2t-1 当x=1>t+1即t<0时, 对称轴在区间右侧, f (x)在[t, t+1]递减,g (t ) = f (t+1) = t2-2. g (t) = 3、其它函数是否也可以利用函数图象的单调性解决在闭区间上的最值问题?如: (1)y= ( 2 ) y= k |x| (k ( 3 ) y= x+ ( 4 ) y= ( 5 ) y= ln(1+x)-x, x ( 6 ) y= cos2x+sinx, x 以上除(1)是反比例函数,学生比较熟悉外,其余的函数可以借助图形计算器作图观察,与二次函数在闭区间上的图象比较,可看出此类函数可以用函数的单调性解决在闭区间上的最值问题,同时观察到函数在闭区间上取最值时,如果不在闭区间的端点处取,就是在单调性的转折点处(极值点,为以后利用导数求最值打下基础) 由于素质教育和创新的观念逐渐深入人心,才促使教学方式由传统的传授式、变相的 灌输式向新型的互动式、探究式转变,图形计算器无疑为这一转变过程提供了良好的载体和有力的工具.因为图形计算器可以帮助学生把问题形象化,验证他们的假设及探索解决问题的不同方式,所以它为积极主动地学习提供了便利.在现代技术条件下,数学概念可以用数字的、图形的和符号的方式来表示;数学问题也可以用以上方式来解决,这就是多重连环表示法.通过多重连环表示法的运用,可以提高学生问题解决的能力和数学理解力,而从认知的角度来讲,学生对自己探究的问题解决的方法更容易记住.同时,现代教育技术手段的应用,为打破传统的教学模式(教师讲学生听)开辟了宽敞的道路.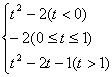
![]() (k
(k![]() 0), x
0), x ![]() [2 ,4]
[2 ,4]![]() 0), x
0), x ![]() [-1 1]
[-1 1]![]() (k>0), x
(k>0), x![]() [
[![]() ,k]
,k]![]() (隐含x
(隐含x ![]() [4, 5])
[4, 5])![]() [-
[-![]() ,1]
,1]![]() [-
[- ![]() ,
,![]() ](换元为二次函数)
](换元为二次函数)