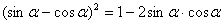提要 利用计算机进行数学实验,让学生通过动手实践,掌握 sinα+cosα的值与角α之间的内在联系.加深学生对基础知识的理解,并能在解题中进行应用.
主题词 数学实验 猜想 证明
一 实验预习题
已知sinα+cosα=![]() ,
,![]() ,求
,求![]()
二 实验目的:通过让学生动手实验,理解角![]() 的终边所在的位置对sinα+cosα取值的影响,让学生能在今后解题过程中,能根据sinα+cosα的值确定角
的终边所在的位置对sinα+cosα取值的影响,让学生能在今后解题过程中,能根据sinα+cosα的值确定角![]() 所在的象限这一隐藏条件.
所在的象限这一隐藏条件.
三 实验工具:几何画板
四 实验过程:
(一) 打开几何画板,建立直角坐标系,并在坐标平面作出一个单位圆;
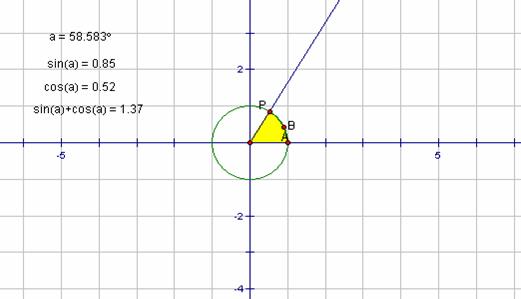
(二) 在第一象限的单位圆圆弧上取一动点P,以原点O为端点,作射线OP,记单位圆与x轴正半轴交于点A,在点A与点P 之间的弧上取一点B,过点ABP 画弧ABP, 标记弧的内部;
(三)选中弧ABP, 度量弧ABP所对圆心角的度数并记为![]() ,计算
,计算![]()
(四) 轻轻拖动圆上的动点P, 观察![]()
表一
|
|
|
|
|
|
|
一 |
26.103° |
0.440 |
0.898 |
1.3380 |
都大于1 |
|
35.277° |
0.578 |
0.816 |
1.3939 | ||
|
44.975° |
0.707 |
0.707 |
1.4142 | ||
|
64.890° |
0.905 |
0.424 |
1.3299 | ||
|
二 |
105.376° |
0.964 |
-0.265 |
0.6991 |
在-1到+1之间 |
|
134.578° |
0.712 |
-0.702 |
0.0102 | ||
|
148.219° |
0.527 |
-0.850 |
-0.3234 | ||
|
167.177° |
0.222 |
-0.975 |
-0.7531 | ||
|
三 |
192.672° |
-0.219 |
-0.976 |
-1.1950 |
都小于-1 |
|
213.742° |
-0.555 |
-0.832 |
-1.3870 | ||
|
224.506° |
-0.701 |
-0.713 |
-1.4142 | ||
|
242.502° |
-0.887 |
-0.462 |
-1.3487 | ||
|
四 |
288.921° |
-0.946 |
0.324 |
-0.6217 |
在-1到+1之间 |
|
307.448° |
-0.794 |
0.608 |
-0.1859 | ||
|
331.238° |
-0.481 |
0.877 |
0.3954 | ||
|
351.610° |
-0.146 |
0.989 |
0.8434 |
(五) 观察以上数据,写出实验结论或猜想;
表二
|
当 当 当 当 |
五 实验证明:
用数学知识推导证明实验所得结论或猜想.
|
证法一:利用几何方法 当角
综上所述,当 当角 其余当角 证法二:利用代数方法 先引入辅助角, 当
. 当 |
表三
六 实验推广:
(一).![]() 的取值范围与角终边所在象限有何联系?
的取值范围与角终边所在象限有何联系?
答:当![]() 在第一象限时,
在第一象限时,![]() ;
;
当![]() 在第二象限时,
在第二象限时,![]() ;
;
当![]() 在第三象限时,
在第三象限时,![]() ;
;
当![]() 在第四象限时,
在第四象限时,![]() .
.
(二).![]() ,
,![]() ,
,![]() 三个式子之间有何联系?
三个式子之间有何联系?
答:三个式子中,只要知道其中一个就可求出另外两个式子.其关系为:
![]() ;
;
![]() .
.
七 实验反思:
本案例是提供给学生的一个实验报告,在学生的实践中主要出现了以下几方面的问题:
(一)几何画板是一个功能十分强大的软件,在学生动手进行实验前应对学生进行系统的培训.如在本实验中,学生要能够利用[编辑]中的(参数选项)对实验中各数据的精确度进行调整,以便在观察数据时得到更准确的猜想或结论.
(二)在整个实验中要充分体现教师的引导作用.本实验不仅可让学生学会发现数学中的隐含条件,如预习题中条件![]() ,实际已告诉我们角
,实际已告诉我们角![]() 只能是锐角,为解决整题提供了一个重要条件.还可以帮助学生复习三角函数中的符号法则,及研究角
只能是锐角,为解决整题提供了一个重要条件.还可以帮助学生复习三角函数中的符号法则,及研究角![]() 终边位置与
终边位置与![]() 的大小.教师在实验中既要帮助学生解决软件使用中碰到的技术问题,更主要的是鼓励学生多动脑,多动手.引导学生获得对所学知识的更深层次的理解,点燃学生思维的火花,提高学生学数学,做数学,用数学的意识.
的大小.教师在实验中既要帮助学生解决软件使用中碰到的技术问题,更主要的是鼓励学生多动脑,多动手.引导学生获得对所学知识的更深层次的理解,点燃学生思维的火花,提高学生学数学,做数学,用数学的意识.
(三)数学实验是我们在课改实验中的一种尝试.它首先要求教师要先过软件操作这一关,而这正是中学教师的弱点,对中学教师进行几何画板,TI图形计数器等软件的系统培训是推进课改的必要措施.其次,教师的教学不应仅停留在课堂上,而要延伸到课外.教师要做到能“导”,会“导”,因此提高教师本身的专业素养也是势在必行.
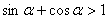 ;又
;又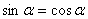 时“=”号成立.即
时“=”号成立.即 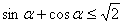
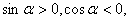 用三角函数线可知,三角形两边之差小于第三边即可证
用三角函数线可知,三角形两边之差小于第三边即可证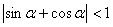 ,即-1
,即-1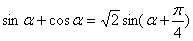 ,
,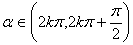 时,
时,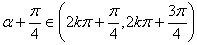 ,
,