对服从二项分布的随机变量取值概率的探索

主题词 信息技术 差异 关系

人民教育出版社《全日制普通高级中学教科书（试验修订本）数学第三册（选修II）》（下称《修订本》）“习题1.1”中有这样一道题：

如果ξ~ B（20，），求使P（ξ＝k）取最大值的k的值．一般地，如果ξ~B（n，p），其中0< p <1，讨论当k由0增大到n时，P（ξ＝k）的变化情况．k取什么值时，P（ξ＝k）取最大值？

在这道题的基础上，人民教育出版社《普通高级中学实验教科书（信息技术整合本）数学第三册》（下称《整合本》）“1.1离散型随机变量的分布列”中设置了这样一个数学实验：

用计算器或计算机研究：

（1）如果ξ~B（20，），求使P（ξ＝k）取最大值的k的值．

（2）如果ξ~B（n，p），其中0< p <1，讨论当k由0增大到n时，P（ξ＝k）的变化情况．k取什么值时，P（ξ＝k）取最大值？

（3）如果某射手击目标的概率为0.7，那么射击10次，他最可能命中几次？

在完成上述习题之后，对分别使用《修订本》和《整合本》的两个平行班进行了对比分析．两个班是同一名教师任教，使用《修订本》的甲班共有56名学生（男生30名，女生26名），他们在这部分内容的教学和完成习题时均未使用信息技术；使用《整合本》的乙班共有53名学生（男生29名，女生24名），他们在学习这部分内容和完成习题时均使用了信息技术．两个班解决同一问题的情况如下：

一、两个班完成情况的对比分析

由于《修订本》中这道题的两个问题就是《整合本》中这个实验的前两个问题，所以分别对学生解决这两个问题的情况进行了统计分析．

（一）问题1的对比分析

表1 问题1列联表

　　相应的三维柱形图如图1所示．图1显示，使用信息技术与解决问题1有关．

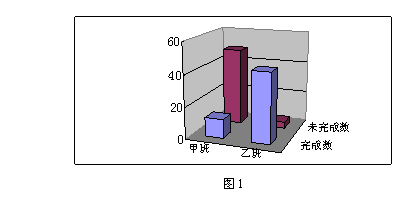
根据表1，可以得到K² ≈ 55.736>6.635．这说明，对这两个班的学生来说，有99%的把握认为，使用信息技术与解决问题1有关，是否使用信息技术对问题1的解决是有显著差异的．

由于问题1的本质就是，考察在k取不同值时大小．而解决这一本质问题，利用信息技术不仅方法很多，而且很方便；利用纸笔却很烦琐，据了解，甲班很多学生正是因为繁琐就放弃了．类似这样的问题，在数学教科书中很普遍．由此我们可以认为，引导学生在数学学习中坚持使用信息技术，对其解决数学问题、提高学习效率是有促进作用的．

（二）问题2的对比分析

表2 问题2列联表

相应的三维柱形图如图2所示．图2显示，使用信息技术与解决问题2有关．

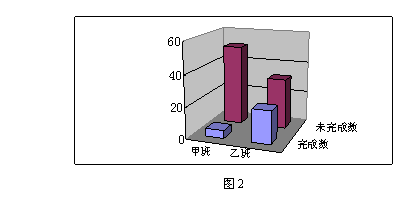
根据表2，可以得到K²≈ 14.124>6.635．这说明，对这两个班的学生来说，仍有99%的把握认为，使用信息技术与解决问题2有关，是否使用信息技术对问题2的解决是有显著差异的．

接下来，进一步分析在解决了问题1的基础上使用信息技术与解决问题2的关系．

表3 问题2与问题1列联表

相应的三维柱形图如图3所示．图3显示，在解决了问题1的基础上使用信息技术与解决问题2无显著关系．

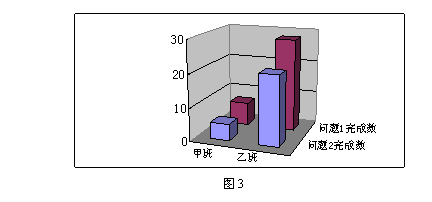
根据表3，可以得到K²≈ 0.003．这说明，对这两个班的学生来说，没有把握认为，在解决了问题1的基础上使用信息技术与解决问题2有关，是否使用信息技术对问题2的解决无显著差异的．

通过对表1和表2的分析，却得到了与表3截然不同的结果．这是因为问题1是问题2的特殊情况，二者有着必然的联系，而根据对表1的分析，使用信息技术又与解决问题1有关，所以才有对表2的分析结果．但对表3的分析让我们知道，解决问题2的关键并不是信息技术的使用，而是问题1的铺垫作用．使用信息技术则是通过与问题1的关系才间接地影响到问题2的解决．由此可见，我们可以鼓励学生使用信息技术探索一些与问题1类似的具体问题，进而受到启发，由特殊到一般地去发现一般问题的结论；但要推理一般性的结论，仅靠信息技术的帮助是不够的．

二、后期完成相关问题的对比分析

两个月后进行了一次检测（不允许使用信息技术），其中有这样一道相关的题：

如果某同学在12码线投篮的命中率为0.5，那么投篮15次，他最可能投中的次数是 ．

在解决了前面的两个问题之后，紧接着两个班的学生都做了几道与《整合本》1.1数学实验第（3）题类似的题，并且正确率都差不多．但在这次检测中，两个班解答这道题的情况却出现了明显的差异．

表4 检测题列联表

　　相应的三维柱形图如图4所示．图4显示，平时使用信息技术与解决这道检测题存在显著关系．

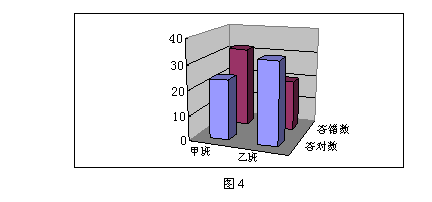
根据表4，可以得到K²≈ 4.111>3.841．这说明，对这两个班的学生来说，有95%的把握认为，平时使用信息技术与解决这道检测题存在显著关系，是否使用信息技术对这道检测题的解决是有显著差异的．

由于信息技术为学生进行数学实验，探索和解决数学问题提供了帮助，并在解决问题的过程中，创造了图象、表格、式子等多元联系表示的认知环境，所以就加深了学生对概念的理解，使知识得到巩固和加强．

三、对使用不同信息技术手段的对比分析

是否使用信息技术对前面问题的解决以及相关知识的掌握都存在明显的差异，那么使用不同技术手段的学习情况又怎样呢？

乙班在完成《整合本》1.1的数学实验时，用到的信息技术有科学计算器（下称A），TI-92Plus图形计算器中的代数功能（下称B）、作图功能（下称C）、表格功能（下称D），计算机中的Excel软件（下称E）．

（一）利用不同信息技术手段解决问题1的对比分析

利用不同信息技术手段解决问题1的情况如下：

表5 不同手段解决问题1表

　　教师对在解决问题1时出错的4名学生作了了解．

1．用科学计算器出错的那名学生是因为输入的式子较长，在计算了k＝6时的值后，再计算k＝7时的值时，只将输入计算器的式子“20 nCr 6*（1/3）^6*(2/3)^14”中的两个“6”改为“7”，而未将“14”改为“13”．

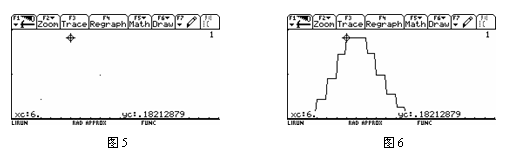
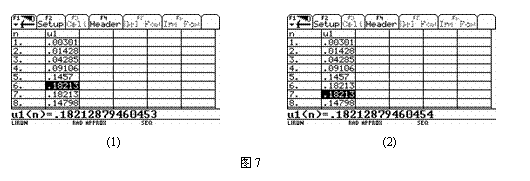
2．用图形计算器的作图功能出错的那2名学生，1名是因为错误地通过作函数y＝的图象研究（图5），结果只得到了k＝6一个值；另1名是因为错误地通过作函数y＝，x?Z的图象研究（图6），结果不仅得到了k＝6，7两个值，还多了一个k＝8．

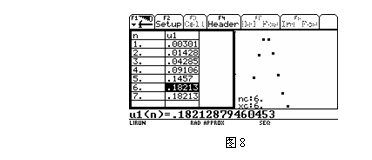
3．用D出错的那名学生是因为发现精确到小数点后13位时，表格中k＝6时的值小于k＝7时的值（图7），于是不加以验证就作出了k＝7的结论．

由此可见，虽然同一问题可以选择不同的信息技术加以解决，但使用不同的信息技术解决问题的效果却不尽相同，如利用科学计算器做一些简单的计算很方便，但做一些较为复杂的运算就容易出错；要能选择适宜的信息技术解决问题，学生首先要对问题所涉及的数学知识有清楚的认识，如将问题1转化为一个数列的问题尚可，但转化为一个连续函数问题，用图形计算器作图研究就出错了；使用不同的信息技术所得结果的精度不同，在解决问题的过程中，应将信息技术的使用与严格的推理验证相结合，如图7，虽然利用图形计算器的表格功能得到的两个值不相等，但若加以验证，就可避免由于技术精度带来的错误．

（二）利用不同信息技术手段解决问题2的对比分析

根据表3我们知道，由于问题2的解决需要严格的推理论证，所以是否使用信息技术对问题2的解决无显著差异的．但学生解决这一问题的思维过程大多是：

如果按照这一过程，将问题2的解决分为利用信息技术探索出结果和给出证明两部分，那么乙班利用信息技术探索出结果的情况为：

表6 利用信息技术探索问题2结果表

　　其中分别用A、B、C、D的为单一表示，用CD（图8）和E（图9）的为多元联系表示．

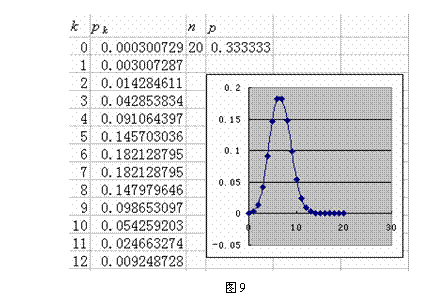
现在将用A、B、C、D的作为一类，用CD和E的作为另一类，列表分析．

表7 两类探索问题2结果列联表

相应的三维柱形图如图10所示．图10显示，使用信息技术进行多元联系表示与探索问题2的结果有关．

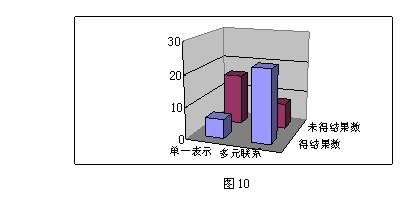
根据表7，可以得到K²≈ 11.434>6.635．这说明，对使用两类不同信息技术的学生来说，有99%的把握认为，多元联系表示与探索问题2的结果有关，是否使用信息技术进行多元联系表示对问题2结果的探索有显著的差异．

利用信息技术将所研究的问题进行多元联系表示，通过图象将隐含的直观地规律体现出来，并联系表格对体现出的规律进行准确的刻画，并利用动态变化的技术对发现的规律进行确定或修改，这使得多元联系表示比单一表示更能够促进学生的思维，更容易探索出需要研究的结果．

通过对使用两种版本的学生探索服从二项分布的随机变量取值概率的比较研究，使我们从一个侧面看到，利用不同手段进行数学学习会产生差异，而且不仅是使用信息技术学习和不使用信息技术学习会产生差异，使用不同的信息技术学习同样也会产生差异．不过，囿于抽取的样本容量较小，所针对的也只是个别数学问题，所以得到的结论不一定具有普遍性．但从两个对比班所反映出来的问题却是真实的，这就值得我们关注了．