内容提要 本文通过信息技术在三角函数教学中 “j对函数y＝Asin（wx+j）图象的影响”这个内容的前后三次教学方式的对比思考，试图阐明：在数学教学中信息技术与数学课程教材的整合“必须以恰是恰地的应用和体现数学的本质”为最终目标，才能实现让学生的思维、解决问题的方法得到发展．否则只能收到适得其反的效果．本文选取了在三角函数教学中作者在实际教学中的三次经历，以案例的形式突出在信息技术下，学生对于数学知识的发现、数学本质的体现、学生的思维发展、信息技术的作用相融合的研究过程.
主题词 多元联系表示 数学本质 信息技术与教学内容整合
一、对过去教学的思考
关于“y＝Asin（wx+j）的图象”这个内容，作为学生，我在传统的教学方法中学过，作为教师，又运用传统的方法教过.当图形计算器、几何画板引进后我高声呐喊：“图形计算器是研究函数图象性质的利剑”．课堂效率提高了，学生的学习主动性调动起来了．2000年、2002年，我曾经两次运用信息技术（TI-92plus图形计算器）对该内容进行教学，在课堂练习中，同一道练习题学生的表现引起我深深地反思，(题：先将函数
图象上的点纵坐标不变，横坐标伸长为原来的2倍，再将图象向右平移
个单位，则所得图象的解析式A.
B.
C.
D.
)这道题学生做对的只占百分之十．这究竟是什么原因呢？
(一) 对第一次教学的反思：
1、教学简要过程
学生活动：利用TI-92PLUS图形计算器,在同一坐标系中固定A、ω的取值，分别作出j取不同值时的函数图象，如图1．固定A、j的取值，分别作出ω取不同值时的函数图象，如图2．
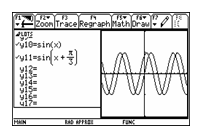
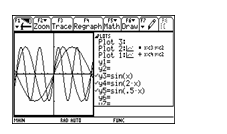
图1 图2 图3
教师活动：利用TI-92PLUS图形计算器向学生展示j、ω变化时的动态图象，然后引导学生总结规律，如图3．
2、教学反思
通过课后对学生进行调查发现：学生无论是通过对图象动态或静态的观察，只能得出“j的符号与函数图象的平移方向的相关性”的正确结论．但对j的数量与平移单位之间的联系却无法通过观察得出．而教师活动中的动画展示也仅仅起到相对于学生的“静态”研究“好看”的效果，图象变换的数学本质：“图象变换依赖于解析式中的参数变化”并没有得到真正的反映，没有完全达到我们的教学目的．看似精彩的课堂为什么没有收到预期的收效？很明显，这无疑说明把技术与该教学内容作这样的整合是低层次的，并没有很好反映出图象变换的数学本质，反思本次教学，其根本问题在于信息技术与教材内容的整合理念没有认真贯彻.
(二) 对第二次教学的反思：
1、教学简要过程
学生活动:在同一坐标系中固定A、ω的取值，分别作出j取不同值时的函数图象．
例如：y＝sinx与y＝sin（x+）的图象
教师活动:让学生思考在两条图象上应取两个满足怎样条件的点、又怎样观察，以此研究j的变化对函数y＝sin（ωx+j）图象的影响？并及时指导学生解决这一问题所需的信息技术．
学生活动:通过技术手段而实现规律的发现，思考这一现象的数学本质并进行归纳总结，如图4．
图4
2、教学反思
第二次教学相对于第一次教学的根本进步在于：对图象变换研究的着眼点是通过图象上点的坐标的数量变化与图象的变换形成联系，有助于学生对j的数量与平移单位之间的联系得出正确结论．
虽然两次教学中运用信息技术的理念发生了深刻的变化，但在课后的教学反思中觉得，在信息技术的环境下，自己还是没有很好地通过问题情景的设计引导学生进行学习，具体表现在学生的认知过程比较单一，“多元联系表示”的认知方式还没有充分落实．学生对函数图象变换的本质：“参数变化引起图象上点的坐标的数量变化”还没有很好掌握，结果导致反馈欠佳．
两次教学后的反思使我感到在信息技术的环境下的教学设计必须要以“帮助学生能更好体会和认清数学本质”为出发点，而恰时恰点的问题情景的设计和信息技术的利用又是解决的主要手段.2005年4月11日我在昆明第一中学高一四班又上此课一堂，对技术与教学整合的观念的不断进步，使我终于有了成功的感觉.
二、“多元联系表示”下的知识构建：
（一）提出问题：
教师：（利用CBL系统向学生展示低压交流电电压随时间的变化关系）刚才我们观察到低压交流电电压随时间的变化关系图象，如图5．同学们想一想这个变化关系与y＝sinx的图象有无关系？
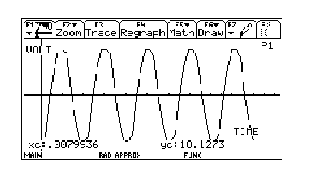
图5
学生：是将y＝sinx的图象进行了某些变化后得到的，具体来说图象在横向和纵向上都发生了变化．
教师：今天我们一起研究函数y＝Asin（wx+j）中参数A、w、j对函数图象的影响．(写出课题)对于这两个函数图象之间的关系你打算采用什么方法去研究？
学生A：对A、w、j取不同的值，固定其中两个，用图形计算器分别作出它们的图象，根据图象归纳出结果，然后运用从特殊到一般的思想，就可得到A、w、j三个系数对正弦型函数的影响．
学生B：我有不同的意见，用上述方法我实验过，A、w的数量变化与图象变化的关系可以根据图象反映与简单的推理就可以得到结论，但j的变化对图象的影响却无法观察得到．所以对于y＝sinx与y＝sin（
）的变化关系的研究可以这样：用“blddata”的功能将y＝sinx图象上各点的坐标采集到数据表格中，如图6，对c3、c4进行变换：c3＝c1+；c4＝c1-（如图6）；用（c5，c2）和（c4，c2）进行描点，将结果与y＝sin（）的图象进行对比，如图7，结果发现将y＝sinx图象上所有点的横坐标都减去 后的图象与y＝sin（）的图象一致．由此发现j的变化对图象的影响．
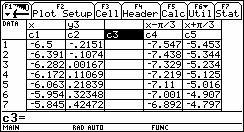
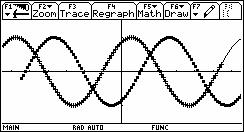
图6 图7
学生丙：我的思考受到前面同学的影响，但和它们所不同的是：我在思考是否可以从最一般的抽象函数f（x）出发去思考解决图象变换的数学本质？具体的想法是：
设（x，y）是函数f（x）图象上的任意点，我们可以解决点（x + j ，y）在与f（x）相关的什么函数图象上，进而可以解决点（wx+ j，Ay）在什么函数的图象上？但目前结果还未最终得出.
学生丁：我准备以函数图象上特殊点的变化作为手段来研究y＝sinx与y＝sin（
）的变化关系，具体过程是：函数y＝sinx图象上的一个最简零点是（0，0），相应于y＝sin（）图象上的一个最简零点是（，0）比较两点我们自然可以得出y＝sinx与y＝sin（）的图象变化关系．用这样的办法也可以解决函数y＝sinx与y＝sin（
）的变化关系.（他的回答得到很多同学的赞叹）
教师：图象变换的本质是坐标的数量变化，比较这三种解决方案，同学甲的方案是我们常用的从特殊到一般的研究方法，但是仅用图形计算器作图观察我们很难发现这种坐标间的数量变化．同学乙的方案是虽然也是从特殊到一般的研究方法，但可贵之处在于通过图象、数据表格的联系，最终发现了图象变换间的坐标关系，我们可以运用图4而达到验证的目的．同学丙的方案是从抽象函数的角度入手，具有一般性的特点，但难度比较大．而这种由一般到特殊的的思维过程又是通过在“特殊到一般”的思维过程中发生、发现而形成的，这种思考方法值得我们认真学习．同学丁的思考方法是基于对图形的变换的考察是着眼于对某些特殊点的坐标变化过程的分析、思考、发现，这是一种很普遍的数学思考问题的方法.
就这样，曾经以为很快就可以解决问题的一堂课在学生运用信息技术的积极参与下内容和方法变得丰富多彩、内涵深刻．在课堂练习中，我又把那道曾经让我产生失败感的那道数学题拿了出来，学生在经历了丰富的、高水平的思维过程后，结果有80%的学生得到正确的结果，让我感到很振奋.
三、深刻的感受
《普通高中数学课程标准》中明确提出：“数学在形成人类理性思维和促进个人智力发展的过程中发挥着独特的、不可替代的作用．”而《考试大纲》也指出“数学是一门思维科学，是培养理性思维的重要载体，通过空间想象、直觉猜想、归纳抽象、符合表示、运算推理、演绎证明和模式构建等诸方面对客观事物中的数量关系和数学模式进行思考和判断，形成和发展理性思维.”所以在课堂教学时，教师要让学生运用多种数学思维方式对数学对象进行数学地思考，在不断地思考与思辩中逐步形成和发展理性思维.函数的各种变换，都是对自变量x或函数值y进行的变换，对应于函数的三种表示形式：解析式、图象和表格，函数变换也可以呈现为三种形式：代数变换（将x变换成wx+j）、图象变换（平移或伸缩）、数值变换（列表表示函数y＝sinx与y＝Asin（wx+j）的关系在数值上的变化）.从一种角度出发而设计的思维过程往往只能认识对象的孤立的静态的特征，只有在信息技术构建下的“多元联系表示”的数学学习环境中，才使得引导学生有意义地把几种表示法中的信息组合在一起，使不同方面建立起概念性联系，从而深刻、全面地理解概念成为可能．这才是“多元联系表示”的教学所要求达到的最终目的．