“TI技术”下的“数学研究性教学”

主题词 信息技术 研究性学习 创新及探究能力

研究性学习是一种新的学习方式，强调学生的主动探究能力，而教学过程是“教”与“学”的有机结合，学生的“研究性学习”无论在课内还是课外，都是在教师的指导下进行的．因此，开展“研究性学习”的教学改革，从教学角度进行研究，把“研究性学习”渗透到课堂教学之中，具有重要的实践意义．

一、结合“两个正数的均值不等式的应用”的教学，谈谈我在“研究性学习”教学的有益尝试．

1、创设问题情景，挖掘知识的内含

数学问题的提出，是知识产生的重要环节，教学中应力求“问题”提的自然、适时，而不是教师的“一厢情愿”．在教学中应提倡允许学生犯错误，从错误中发现问题，去探求问题的实质．这种由错误走向真知的学习更有意义，学生对知识的掌握更深刻．因此，教学中可采用展示问题，让同学的错误成为问题的导火索．

在学习“两个正数的均值不等式及简单应用”后，提出如下问题：

问题1:求函数y=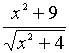的最小值.

同学们对问题1思考后，认为函数的解析式中分子、分母均为正数，试图用“均值不等式”处理，但似乎又不能直接使用，小组讨论后，有的同学想到最小值的问题，最好出现“≥”某个常数，于是提出把解析式化为“和”的形式，即：，当x= ±1时,取“=”， 问题获解．此时，可即时强化一“正”二“定”三“等”求最值的条件．

问题1的获解，同学们信心培增．此时，抓住时机给出问题：

问题2：求函数y=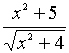的最小值.

同学们不加思索：一样的解法．教师不动声色，请一个同学来解答，解答如下 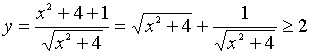：，最小值为2，再问：对吗？有的同学迟疑了一下，提出“等号”不成立，因为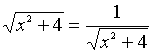无实数解，再问：函数 y=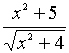由“均值不等式”只能得y＞2 ，是不是没有最小值呢？学生不置可否，一片茫然，此时，教师可用计算机的“几何画板”给出函数 y=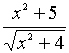的图象．（图1）

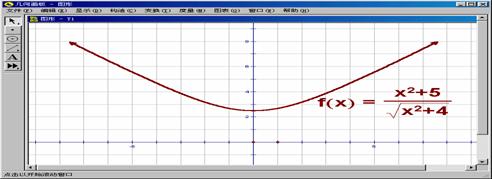
图1

学生从函数图象看到有最低点，函数应该有最小值．“均值不等式”的等号失效了，怎么求呢？学生的认识发生冲突，抓住冲突，提出问题的时机已经成熟．抛出研究问题：均值不等式“等号”不成立，怎么办？

2、认知归纳，呈现思维．

引导同学思考：利用了数形结合的思想方法，函数 y=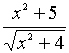从图象上看出有最小值．我们可作变形：令t=（t≥2）, 则y= t +．下面我们来探究y= t+（t≥2）的性质，从哪里入手，有同学提出“图象”，教师用计算机绘出图象（图2）

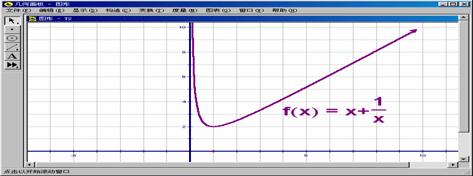
图2

引导同学们观察图象，得出：y=x+在(2，+∞)上是增函数，请同学用增函数的定义给出证明，可强调证明单调性的过程，其实就是不等式的比较法，可增强学生新、旧知识的内在联系，问题2获解，当t=2即x=0时，y_min=．不能就此罢休，教师可引导：y=x+( x > 0 ) 的单调性如何？学生观察图象后获得：y=x+在(0 , 1)上是减函数，在(1，+∞)上是增函数．其实问题2中t∈(2，+∞)是(1，+∞)的子区间，由此可处理形如 y=x+（x≥a，a＞1为常数）或 y=x+（0＜x≤a，a＜1的常数)的最小值问题．

3、层层推进，由特殊到一般，让学生体验数学研究的艰辛与喜悦．

科学规律的发现往往是由一个特殊问题引发的，由特殊获得启发，去探寻一般规律，是科学研究的重要方式，学习中我们不能仅满足于就题论题，而应引导学生学会研究问题，探寻知识．

探讨了y=x+( x > 0 )的性质后，再进一步提出系数不为“1”的呢？即y=ax+(a, b > 0, x > 0)的单调性又如何呢？此时，同学自然会想到“以形助数”，用计算机给出含参数a，b的动态图象图3，让学生观察a，b常数变化，单调区间怎么变？

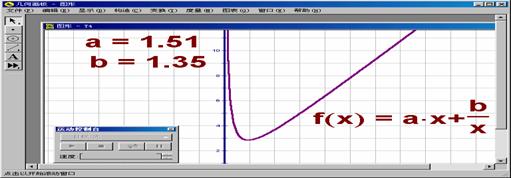
图3

参数a，b的不同取值，同学容易看出单调的特点不变：图象先下降后上升．但分界点随a，b在变，说分界点与a，b有关，它们有何数量关系，可用图形计算器做下列数学实验，让学生认识、归纳．

通过实验观察，得出分界点的横坐标是，让学生给出证明：y=ax+在(0,]上是减函数，在[, +∞ ）上是增函数，从而获得“均值不等式”不能取“=”用函数 y=ax+的单调性解决的一般规律．

4、从理论到实践，增强应用意识和数学研究的成就感

数学源于实践，又服务于实践，数学的灵魂在“应用”，在“学数学”中“用数学”，不仅培养学生学习数学的兴趣，而且对增强学生的应用意识和创新能力有着重要意义．

在探讨y=ax+(a, b > 0, x > 0)的单调性的基础上．可结合“信息技术与高中数学教材整合”给出应用,变式为：

题3：某工厂要建造一个长方体无盖贮水池，其容积为4800㎡，深为3m，由于地形限制，宽不能超过30米，如果池底每1㎡的造价为150元，池壁每1㎡造价为120元，问怎样设计水池能使总造价最低，最低总造价是多少元？

题4：甲、乙两地相距S千米，汽车从甲地匀速行驶到已地，速度不得超过c千米/时，已知汽车每小时的运输成本（单位：元）由可变部分和固定部分组成：可变部分与速度v（千米/时）的平方成正比，比例系数为b；固定部分为a元

（1）把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出这个函数的定义域．

（2）为了使全程运输成本最小，汽车应以多大速度行驶?

由此可渗透均值不等式求最值的三个条件和分类讨论的思想方法，让学生在应用规律解决问题中感受到研究的价值，认识研究的问题在实际中无处不在，而不是空穴来风，进一步感悟数学的价值，而不是空洞、枯燥的知识．

二、“研究性学习”教学实践的启示.

“研究性学习”以培养学生的创新意识和探究能力为主要目的，其核心在于“研究”．因此，如何有效地使用教材内容，挖掘数学素材，使用“研究性学习”的方法，在教学中培养学生的创新意识和探究能力，成为课堂教学改革的重要方向．

“研究性学习”的教学具有以下特性：

1、学生学习的自主性

自主学习是相对于传授性学习而言的，主要体现在学习的主动性，在课堂教学中的积极参与程度．因此，课堂教学过程中应强调学生的主体性，充分发挥学生的个体作用，促进学生的个体发展，让每个学生在教学活动中尽可能做到自己采集信息、处理数据，问题自己提出，提倡独立钻研，独立思考，别出心裁，以培养独创精神．

2、学生学习的合作性

学生个体在解决问题的过程中，往往会遇到困难，通过学生间的思维沟通，相互合作，取长补短，往往会使困难得以克服，加快解决问题的速度．增强学生的研究信心，培养学生的协作意识和团队精神，提高与人沟通和交流的能力，这种以“学习小组”为主的合作学习，有利于培养学生的团队精神和竞争意识．

3、学生学习的研究性

“研究性学习”的本质是“研究”，“研究性学习”的教学不同于讲授式，也不同于自学式，其主要过程是：提出问题→研究探索→得出结论．提出的问题是开放的，只有素材而没有结论，而“研究”应体现出方法性，不能盲目进行，在研究的过程中，应教给学生一些研究的基本方法，在“研究性学习”的教学活动中，最常用的研究方法有：归纳性研究方法、类比性研究方法、试验性研究方法、实验性研究方法等．

“研究性学习”为数学教学的改革提供了一种新的模式，强调学生的自主性和探究性．知识的获得不再是“你”教“我”学，而是师生共同探索发现的结果，需要教师转变观念，大胆实践，创设更多的情景，培养学生善于质疑、乐于探究、主动发展、努力求知、以人为本，充分发挥学生的主体作用，培养学生自主学习、主动探究的学习习惯，把“课改”落到实处．