简单线性规划是教科书中的新增内容，从教学情况看，有不少学生对线性目标函数的最优解的确定存在诸多疑惑，笔者根据教后的体会，从以下几个方面例说给读者，从而达到拓宽解题思路，提高解题能力的目的。
一、 理论问题线性目标函数的最优解的探求
例：解线性规划问题，求Z = 3 x + y的最大值，使式中的x、y满足约束条件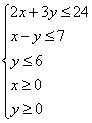
。
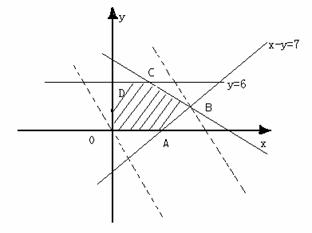
解：作出可行域，如图五边形OABCD表示的平面区域，作出直线L0 ：3x + y = 0 ，将它平移至点B，显然，点B的坐标是可行域中的最优解，它使Z = 3 x + y 达到最大值，解方程组
得点B的坐标为（9 ，2），∴Zmax = 3×9 + 2 = 29
通过这个例子，可以得到下面的规律：在线性条件不变的情况下，可行域中最优解对应点在何处，与目标函数Z = ax + by + c （a≠0，b≠0）所确定的直线L0： ax + by + c = 0 的斜率有关：
1、 当
时：
（1）若
，线段BC上所有点的坐标都是使Z取得最大值的最优解（最优解有无穷多个）；
（2）若
，点B的坐标（9，2）是最优解；
（3）若
，点C的坐标（3，6）是最优解。
2、当
时的不同情形留给读者自己完成。
二、 利用格点法求整数解
有些应用题是在可行域里寻找整数解，在有限范围内可直接作图找出格点（对靠近边界的个别点是否符合，可代入线性约束条件检验，作出合理的取舍）
例1：配制A、B两种药剂，需要甲、乙两种原料，已知配一剂A种药需甲原料3mg，乙原料5mg；配一剂B种药需甲原料5mg，乙原料4mg，今有甲原料20 mg，乙原料25mg，若A、B两种药至少配一剂，共有多少种配制方法？
解：设A、B两种药分别配x、y剂，（x、y∈N+ ），由题意，则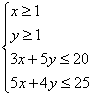
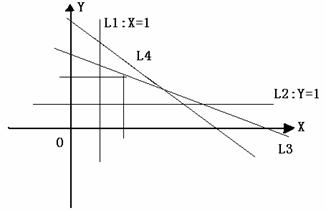
作出可行域，是一直线L1 ：x = 1 ， L2 ：y =1 ， L3 ：3x + 5y =20， L4：5x + 4y = 25 围成的区域。
∵ x、y ∈N+
∴ 在区域内作出所有格点（整数点），由图知区域内的所有格点为（1，1），（1，2），（1，3），（2，1），（2，2），（3，1），（3，2），（4，1）。共8个点，所以在至少配备一剂的情况下，共有8种不同的配制方法。
三、 先“估计”后“核实”求最优解
为了寻找最优解，有时在边界上找不到，得要在边界交点（区域顶点）附近寻找最优整数解，单凭现图观察往往粗糙而不准确，通过区域顶点的目标值适当放缩---估计，然后通过解不等式（组）探求最优解──核实。
例2：有同一批规格钢条，有两种切割方式，可截成长度为a的两根，长度为b的3根，（1）现需2根a长与1根b长配成一套，问按两种方式进行切割应满足的比例是多少？（2）如果长度为a的至少需50根，长度为b的至少需45根，问如何切割可使钢条用量最省？
解：设第一、第二种分别切x、y根同规格的钢条，则长为a的有2x+3y根，长为b的有3x+y根。
（1） 配套的话：
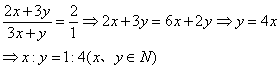
一、二种截法的比为1：4
（2） 由题意，则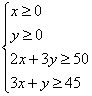
作出可行域
由题意x、y∈N
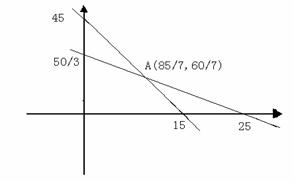
由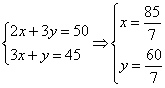
∴ A ( 85 / 7，60/7)
作直线L：x+y=z
∵
∴
当L过A点时：
, 但此时
∴若 x、y∈N时，Zmax=x+y=21 (先估计)
由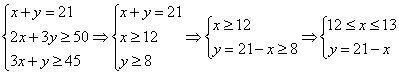
又
∴ 
或
后核实
∴第一、二种分别切13根、8根或第一、二种分别切12根、9根用料最省，都是21根。
从上面的问题解决可以发现，在参数较大的可行域中找整数解，因它有无数个，通常是求最优整数解，在数据较大时难以从图形上观察得出，必须根据斜率比较判断（如）最优解可能是哪一个区域的点，如最优整数解不是最优区域顶点，就得先估计后核实了。
四、 利用不等式探求某些简单规划问题的最优解
例3：某厂使用两种零件A、B装配两种产品x、y，该厂的生产能力是月产x最多2500件，月产y最多1200件，而组装一件x需4个A、2个B，组装一件y需6个A、8个B。某个月，该厂能用A最多14000个，B最多12000个，已知产品x每件利润1000元，产品y每件利润2000元，欲使该月利润最高，需组装产品x、y各多少件？最高利润是多少万元？
解：设月生产产品x、y分别为x件、y件，该月利润为Z，则：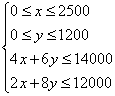
即
目标函数Z=1000x+2000y，即Z=1000（x+2y）
设
，易得
∴
∴
(元)
等号成立的条件是
即
符合条件（1）、（2）
∴最优解为（2000，1000），即组装产品x为2000件、产品y为1000件时，月利润最高，最高利润400万元。
本题若利用线性规划的方法求最优解也是很简便的，而用不等式求解时，主要考虑较复杂的约束条件（如本例中的（3）、（4）），而较简单的约束条件（如本例中的（1）、（2））则用来检验最优解是否符合即可，因此，灵活运用不等式的二元一次不定方程的知识，也能有效突破难点，有时解法更简洁、更易懂。