数学实验案例

主题词 数学实验 案例

谈到实验，大家自然会想到物理实验、化学实验和生物实验，很少有人会把实验与数学联系．其实数学实验也应是数学教学中的重要组成部分．近几年来，越来越多的数学教师开始关注数学实验，本文以一个数学实验设计为例谈几点感受．

实验课题：等差数列前n项和的最值

实验背景：数列是高中数学中的重要内容，数列的概念与运算在日常生活和生产实践中有着广泛的应用．随着现代教育技术的推广，TI图形计算器开始进入我们的教学与课堂，它的序列图像功能可以帮助我们更好,更轻松地学习数列，掌握数列．

实验目的：利用图形计算器探求等差数列前n项和的最值，掌握等差数列前n项和最值的求法

实验仪器：TI图形计算器

实验步骤：

1.打开图形计算器，在状态设置(MODE)中选定GRAPH为Seq作图方式．

2.显示y=编辑器，定义首项为负的递增等差数列{a_n}，输入通项公式a_n及其前n项和公式S_n．

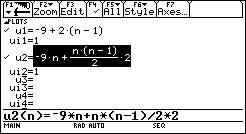
3.显示窗口编辑器，进行窗口设置．

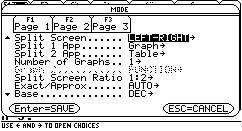
4.屏幕拆分设置，以同时显示表格与数列图像．（在状态设置MODE中选定Spilt Screen为left--right方式，选定Split 1 App为Graph方式,选定Split 2 App为Table方式，选定Split Screen Ratio为1:2方式．）

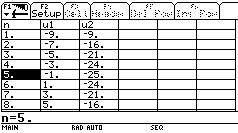
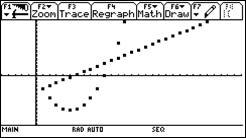
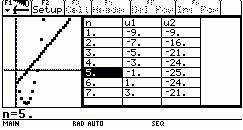
5.观察表格与数列图像，探求当n为何值时，S_n出现最值？

6.定义首项为正的递增等差数列{b_n}，重复步骤2～5．

7.定义首项为负的递减等差数列{c_n}，重复步骤2～5．

8.定义首项为正的递减等差数列{d_n}，重复步骤2～5．

实验数据及现象记录：

1.公差不为零的等差数列中，当公差               时，其前n项和S_n有最               值；当公差               时，其前n项和S_n有最               值．

2.公差不为零的等差数列的前项和S_n关于n的图像是              所以可利用                   来求S_n的最值及对应的项数n．

3.公差不为零的等差数列具有单调性，当公差d>0时，数列单调递              ，如果首项为负，只要将数列中的所有              项相加，即可得S_n的最              值．如果首项为正，则              即为S_n的最              值；当公差d<0时，数列单调递              ，如果首项为正，只要将数列中的所有              项相加，即可得S_n的最              值．如果首项为负，则              即为S_n的最              值．

数学证明：

问题拓广：设等差数列的前n项和为S_n．已知a₃=12，S₁₂>0，S₁₃<0．

(1)求公差d的取值范围；

(2)指出S₁，S₂，…，S₁₂中哪一个值最大，并说明理由．

分析：可计算d∈(-24/7,-3)，不妨取d=22/7，从而可求a₁=128/7．利用图形计算器的序列图像功能和表格显示功能可得到S₆最大．

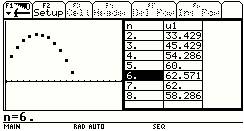
由此，我们不难看出数学实验在传授知识，激发学生学习兴趣，创新教学模式等方面起到至关重要的作用．

数学实验充分展示了数学知识的发现过程．数学事实首先是被猜想，然后是被证实，猜想在数学发现中具有极其重要的意义，如何在教学过程中引导学生进行猜想与合情推理，让学生在发现的过程中掌握数学知识，一直是数学教育界研究的课题．而数学实验正好为学生提供了一个动手“做”数学的平台（“做”即探索）．学生遇到一个数学问题，可以通过计算机及相关数学软件去实验一下，通常这种实验是针对一些具体例子来进行的，如果你有足够多的具体例证表明你的想法的正确性，那么就可以再进一步地通过逻辑推理的方式去证明它，而且证明的思想方法很大程度上已经蕴含在具体例证的获得过程中了．

数学实验充分体现了学生在学习中的主体地位．在实验过程中教师很少直接教给学生数学知识，而是向学生提出问题，并借助计算机为学生创设学习的情境，通过学生之间的互相合作与讨论，不断提出并验证或否定猜想，进而尽可能地给出严格证明．教师在这个过程中所起的是学习的指导者与帮助者的作用，学生才是学习的主人．

数学实验能激发学生学习的积极性和主动性，促使学生变被动接受式的学习为主动参与式的学习．数学实验的工具主要是计算机及相关数学软件（特别是《几何画板》），它能为学生创造出一种图文并茂、丰富多彩、人机交互、及时反馈的学习环境．在这种环境中，学生可以利用信息技术模拟现实情景，构建数学模型，进行数学探究和应用．学生在学习过程中既可看见，又能听见，还可以动手操作．这样，学生学习数学的兴趣可以被更有效地激发，让学生学得更加生动活泼，富有成效．

数学实验能有效地培养学生的创新意识和实践能力．数学实验强调学生的实践活动，让他们在信息技术的帮助下，通过自己的亲身实践而获得数学知识，体验数学思想方法，领悟数学本质．数学实验改变了单纯传授知识、训练解题能力的教学模式，它给学生一个实践和思考的空间，让学生从听数学、学数学到做数学，再到玩数学，从被动学习到主动学习，再到创造性学习，从而有效地培养学生的创新意识和实践能力．