在广东、山东、海南、青海四省依照《高中数学课程标准》实施的高中数学新课程中,如何贯彻新课程理念,正确把握和实施高中数学教学,已成为每一个高中数学教师应该研究的课题。本教学案例选取“进位制”作为“算法初步”的教学内容,以教学设计的形式探索高中数学新课程的实施过程。
一.教学设计意图
1.关注问题性、启发性,加强联系性
本课通过“猜生月生日”这一程序游戏创设教学情景,使学生自然提出问题:“这一程序是怎样设计的?”进而启发学生主动探索程序中的算法算理,从而引进数的进位制及其转化问题。教学过程中,由学生熟悉的十进制出发,引导他们分析得到“除10取余法”,再通过类比得到“除2取余法”,进而推广得到“除k取余法”,从而解决十进制转化为k进制的问题。在此基础上,再研究k进制转化为十进制的问题,最后解决两种不同进位制间的互相转化问题。这样设计的目的,是遵循认知规律,以问题引导学习,体现数学知识的形成与学生认知的过程性,加强数学知识间的联系性,促使学生主动探究,培养学生的创新意识和应用意识。
2.讲背景,讲数学,讲思想,讲应用,
在“猜生月生日”这个真实背景下,学生能真切地体会算法的作用与数学的力量,引入这个背景的意义,在于讲数学中的算法思想,在于应用算法思想解决实际问题。在课的设计与实施过程中,始终围绕“不同进位制间的转化”这一目标,让学生经历由探究算理,到抽象算法步骤,绘制程序框图,再到设计并优化程序的全过程,使学生明确自己是在学数学而不仅仅是在编程序或玩计算机,这一过程的主要目的是使学生得到算法思想的熏陶与提升。课后作业要求学生利用已学的知识与方法探究“猜生月生日”的算法与算理,意在讲应用,让学生关注数学的“源”与“流”,加强数学与事物间的联系。
3.注重数学课程与信息技术的整合,尝试改进教与学的方式
在教学过程中,师生充分利用TI图形计算器一起进行算理探索、程序设计、演示交流,这不仅使学生亲身体验了算法的实现过程,而且为改进教与学的方式提供了强有力的平台。在数学课程与信息技术的整合中坚持贯彻“必要性”、“平衡性”、“广泛性”、“实践性”、“实效性”等原则。
二.教学任务分析
1. 通过“进位制”这一案例的教学,使学生进一步加深对算法含义的认识:
(1)算法通常是指可以用计算机来解决某类问题的程序或步骤(可行性);
(2)算法中的程序或步骤必须是明确和有效的(确定性);
(3)算法中的程序或步骤必须在有限步之内完成(有穷性).
2.通过“十进制转k进制”与“k进制转十进制”的算理分析与程序框图,加深对算法的三种基本结构(顺序结构、选择结构、循环结构)的认识,正确理解与使用循环结构中的选择结构.
3.根据“十进制转k进制”与“k进制转十进制”的程序框图,利用TI图形计算器的程序语言写出程序,由此体会并正确选用算法语句(输入语句、输出语句、赋值语句、条件语句、循环语句)表达算法的步骤与算法的基本结构.
4. 通过“进位制”这一案例的教学,使学生熟悉用算法思想解决问题的基本步骤:
(1)用自然语言写出“算法步骤”;
(2)根据算法步骤写出“程序框图”;
(3)选用一种计算机程序设计语言,根据程序框图写出“程序”;
(4)上机验证程序的可行性,完善和优化算法.
三.教学重点和难点
“十进制转k进制”与“k进制转十进制”的算理分析.
四.教学基本流程

五.教学用具
师生每人一台TI-92PLUS图形计算器,一块TI液晶显示屏,实物投影仪,投影机,投影屏幕.
六.教学情境设计
|
情景步骤 |
师生活动 |
设计意图 |
|
1.“猜生月生日游戏”: “请先依次指出表格(见附注1)中哪些行有你的生月,然后再依次指出表格中哪些行有你的生日,便知道你的生月生日.” |
教师给出生月生日表,并同时讲清游戏规则,然后请一位或两位学生根据表格回答,教师使用编好的TI程序(见附注2)记录学生的回答,学生回答完毕则由程序立即获得学生的生月生日. |
这个游戏中用到的“生月生日表”的制作原理是二进制记数法,它需要掌握“十进制转二进制”的方法;计算生月生日的程序1的算理是“二进制转十进制”的算理,这一过程可以引起学生对游戏的算法的兴趣,从而引入本节课. |
|
2.让学生用TI图形计算器计算:(1)3×103+7×102+2×10+1×1.00;(2)4×103+9×102+3×10+6×100. |
师生一起用TI图形计算器计算,教师的计算结果投影在屏幕上,学生计算完毕后思考一般情况. |
让学生体会十进制记数法的实质,为探究“除10取余”作准备. |
|
3.以3721为例,探究“除10取余”的过程. |
教师启发,学生观察: 3721=372×10+1, 372= 37×10+2, 37= 3×10+7, 3= 0×10+3. |
得出“除10取余”的十进制记数法则(见附注3),为学习二进制的“除2取余”记数法则作准备. |
|
4.以十进制数89为例,探究“除2取余”的过程. |
让学生模仿得出: 89 = 44×2 +1, 44 = 22×2 +0, 22 = 11×2 +0, 11 = 5×2 +1, 5 = 2×2 +1, 2 = 1×2 +0, 1 = 0×2 +1. |
得出“除2取余”的二进 制记数法则. |
|
5.在TI图形计算器上以89实现“除2取余”的过程. |
师生一起进行下述操作: 89→
重复进行上述取余与取商的操作,直至商为0. |
探究“十进制化二进制”算法中的主要算法结构:条件结构与循环结构. |
|
6.从操作过程中提炼出“十进制转二进制”算法步骤,并推广到“十进制转k进制”的算法步骤. |
教师让学生先思考上述操作中的算法结构,然后写出算法步骤并进行交流,最后由教师评析并给出正确的算法步骤. |
得出“十进制转二进制”的算法步骤,并推广到“十进制转k进制”的算法步骤(见附注4). |
|
7. 由“十进制转k进制”的算法步骤写出程序框图 |
让学生写出程序框图并进行交流,随后教师评析 并给出正确的程序框图. |
得出“十进制转k进制”的程序框图(见附注5),进一步领会算法结构. |
|
8.根据“十进制转k进制”的程序框图,在TI-92PLUS图形计算器上编写程序并运行. |
让学生在TI-92PLUS图形计算器上编写程序并运行,以89分别转二进制、五进制,检查学生的程序是否正确. |
这是本节课的一个重要环节,不仅能使学生正确掌握“十进制转k进制”的算法程序(见附注6),还能使学生积极主动并有效地学习. |
|
9.以1011001(2)为例,探究“二进制化十进制”的算理. |
师生一起将“情景步骤4”中的“师生活动”所得到的算式由后往前代入并整理得到:1011001(2)=1×26+0×25+1×24+1×23+0×22+0×21 +1×20=89. |
通过实例体会“二进制转十进制”的算理,为得到“k进制转十进制”的算法程序作铺垫. |
|
10.在TI-92PLUS图形计算器上编写并运行“k进制转十进制”程序. |
让学生在TI-92PLUS图形计算器上编写程序并运行,以1011001(2)、324(5)分别转十进制,检查学生的程序是否正确. |
使学生掌握“k进制转十进制”的算法程序(见附注7),促使学生积极主动并有效地学习. |
|
11.把二进制数1011001化为五进制数. |
让学生先利用“k进制转十进制”的程序得出:1011001(2)=89, 先利用“十进制转k进制”的程序得出: 89=324(5), 所以,1011001(2)=324(5). |
体会任意两种进位制的数之间的转化方法:先“k进制转十进制”,再“十进制转s进制”. |
|
12.讨论与小结. |
让学生讨论、交流对算法的认识及利用算法思想解决问题的基本步骤,教师进行陀造詞归纳小结. |
使学生体会教学任务中所期望的学习目标. |
|
13.教师给出下列作业: (1)了解日常生活中经常用到的进位制,并举一个运用二进制数的例子,体会 二进制数的重要作用. (2)将十进制转k进制、 k进制转十进制的算法步骤、流程图及TI程序整理 成作业. (3)写出“猜生月生日表”的设计原理,完成“猜生月生日”的算法步骤、流程图 及TI程序,并上传到数学论坛“高一(1)、(2)、(3)班”与同学交流. | ||
1.生月生日表:

2.猜生月生日程序:
Birthday()
Prgm
Clrio
For i,1,2
If i=1 then
Disp “month”
Else
Disp “day”
Endif
Disp “ 16 17 18 19 20 21 22 23”
Disp “ 24 25 26 27 28 29 30 31”
Input “1 or 0?”,a
Disp “ 8 9 10 11 12 13 14 15”
Disp “ 24 25 26 27 28 29 30 31”
Input “1 or 0?”,b
Clrio
Disp “ 4 5 6 7 12 13 14 15”
Disp “ 20 21 22 23 28 29 30 31”
Input “1 or 0?”,c
Clrio
Disp “ 2 3 6 7 10 11 14 15”
Disp “ 18 19 22 23 26 27 30 31”
Input “1 or 0?”,d
Clrio
Disp “ 1 3 5 7 9 11 13 15”
Disp “ 17 19 21 23 25 27 29 31”
Input “1 or 0?”,e
Clrio
If i=1 then
a*2^4+b*2^3+c*2^2+d*2+e→m
Else
a*2^4+b*2^3+c*2^2+d*2+e→n
Endif
Endfor
{m,n}→l
Disp “birthday”,l
Endprgm
3.一个十进制数a除以10所得的商是b0,余数是![]() ,即
,即
![]() ,
,
则![]() 是a的个位数;
是a的个位数;
b0除以10所得的商是b1,余数是![]() ,即
,即
![]() ,
,
则![]() 是a的十位数.
是a的十位数.
一般地,![]() 除以10所得的商是
除以10所得的商是![]() ,余数是
,余数是![]() ,即
,即
![]() ,
,
则![]() 是a的从右往左数第n+1位数.
是a的从右往左数第n+1位数.
4.“十进制转k进制”的算法步骤:
第1步:给定十进制正整数a,确定转化后的进位k;
第2步:求出a除以k所得的余数、商,并分别赋值给r、a;
第3步:若a≠0,则重复第2步, 直到a=0;
第4步:将依次得到的余数从右往左排列起来,则得到k进位数.
5.“十进制转k进制”的程序框图:
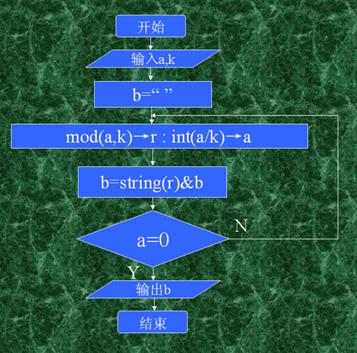
6.“十进制转k进制”的TI程序:
(1)循环结构为当型结构:
g1310520()
Prgm
Clrio
Local a,b,r,k,x
“ ”→b
Input “x(10)=?”,x
Input “k=?”,k
x→a
If a=0 then
string(a) →b
Else
While a≠0
mod(a,k) →r
string(r)&b→b
int(a/k) →a
Endwhile
Endif
b&”(”&string(k)&”)” → b
String(x)&” (10)= “&b → b
Disp b
Endprgm
(2)循环结构为直到型结构:
g1320520()
Prgm
Clrio
Local a,b,r,k,x
“ ”→b
Input “x(10)=?”,x
Input “k=?”,k
x→a
loop
mod(a,k) →r
string(r)&b→b
int(a/k) →a
if a=0 then
exit
endif
Endloop
b&”(”&string(k)&”)” → b
String(x)&” (10)= “&b → b
Disp b
Endprgm
7.“k进制转十进制”的TI程序:
g1330520()
Prgm
Clrio
Local a,b,c,k,n,s,x
0→s
1→i
Input “k=?”,k
Input “x=?”,x
Dim(string(x)) →n
String(x) →a
While i![]() n
n
mid(a,i,1) →b
expr(b) →c
s+c*k^(n-i) →s
i+1 →i
Endwhile
Disp string(x)&”(”&string(k)&”)=”&string(s)”(10)”
Endprgm
八.后记
本案例的设计者根据设计实施了课堂教学,感谢广东省一百多位高中数学老师亲临听课并指导,特别感谢人民教育出版社的宋莉莉老师在听完课后与授课者进行了交流,并给出了如下的评价:
“‘进位制’一课是中学新增的“算法初步”的内容,这堂课的设计与实施,值得我们认真研究和思考。总体看来,本堂课具有较高的教学质量,这与教师的精心设计和学生的配合是分不开的。具体分析,以下几个方面特别值得我们借鉴:
1. 引入精彩,展开自然。能准确猜出学生的生月生日的程序引起了学生极大的兴趣,“这个程序的算理就是本堂课的内容”又把学生带入了课题,而课后作业“设计猜生月生日的程序”既与引入相呼应,又是本课内容的自然应用。
2. 教学重点突出,过程流畅自然。本堂课紧紧围绕“进位制的转换”这个重点,环环相扣,引人入胜。由学生熟悉的十进制出发,引导他们分析得到“除10取余法”,再将这一算法的算理进行迁移,得到“除2取余法”,进而得到“除k取余法”,从而解决了十进制转化为k进制的问题。师生接着研究了k进制转化为十进制的问题,最后解决了两种不同进位制间的互相转化问题。
3. 重视学生的亲身体验,培养学生的算法思想。在教学过程中,师生利用TI图形计算器一起进行算理探索、程序设计、演示交流,使学生亲身体验了算法的实现过程,让学生经历了由探究具体问题的算理,到抽象出算法步骤,绘制出程序框图,再到设计并优化程序的全过程,使学生的算法思想得到了熏陶与提升。”
本文获得“高中数学课程教材与信息技术整合的研究”课题子课题论文和优秀案例评比一等奖