1.问题的提出
我国数学教育由于长期受应试教育的影响,课堂上教师“重灌输式讲授,轻探究式教学”;重有限知识的“学会”,轻无限知识的“会学”,教师习惯通过大量练习来让学生学习数学,这是我国数学教学的基本特征。这显然是一个被动的接受知识、强化储存的过程,忽视了学生在学习过程中的主体性,也就缺乏师生之间、生生之间的互动。随着新一轮基础教育课程改革的不断深人,学生学习方式的转变成为一个很重要的课题。国家教育部2003年4月颁布的普通高中《数学课程标准》中明确提出,“丰富学生的学习方式、改进学生的学习方法,是高中数学课程追求的基本理念”,“学生的数学学习活动,不应只限于对概念、结论和技能的记忆、模仿和接受,独立思考、自主探索、动手实践、合作交流、阅读自学等都应是学习数学的重要方式”。因此,学生学习方式的转变,不仅涉及具体的学习方法、策略等,还应包括其学习是否具有自主性、探究性、合作性等基本特征。培养学生学会学习、促进学生学习方式的转变,应是新课程改革的关键,显得尤为重要。笔者认为,要转变学生的数学学习方式,可以从培养学生“阅读”、“质疑”、“探究”、“实践”和“反思”五方面人手。
2.转变学生数学学习方式的有效途径
2.1 阅读
苏霍姆林斯基说过:“学会学习首先要学会阅读”一提到阅读,很容易让人联想到读文学著作,其实学习数学同样需要阅读,但对于很多学生而言,“上学读书”已被“上学听讲”所取代。在传统教学中,教师往往是将教材中的内容“掰开了,揉碎了”讲给学生听,对学生的“读书”却有所忽视。从长远看,一个人不可能终身依靠教师,教师“教”的目的是为了“不教”,终身学习是时代的发展对我们每一个人提出的要求。因此,培养学生学会学习的基本前提是要学会阅读自学。
首先是学会阅读教材。数学教科书的每一章节,就是一篇逻辑严谨的说明文。教师可先提出问题,让学生带着问题去阅读并回答问题。随着学生阅读能力的提高,可以尝试让学生对课本进行独立阅读、思考、完成作业,进而对课本进行质疑、重组、超越,教师只充当点拨、修正的角色。
比如,在学习“逻辑联结词”这节内容时,我要求学生先读书。这一节分四部分内容:命题、逻辑联结词、复合命题和复合命题的判断。我分别请同学来讲解、讨论和总结。学生通过认真读书,认识了教材中有关的数学术语,理解领会了数学语言(文字语言、符号语言、图表语言),促进了数学语言的内化。在此基础上,我还进一步鼓励学生归纳总结数学思想方法、前后内容的逻辑关系,并大胆地提出自己的看法,充分挖掘内涵。教科书中提到自动控制中有“与门电路”和“或门电路”,有学生提出应该存在“非门电路”。我鼓励学生大胆设计这三个电路,这不仅激发了学生学习的积极性,而且在设计的过程中,学生对“或”、“且”、“非”的理解更深了一层。
除了教材之外,可供学生阅读的数学书籍其实很多。在平时的数学教学中,我结合新教材的特点,有针对性地向学生推荐了大量数学史料书籍、数学名人传、数学期刊杂志、世界名题与趣题的简易读本等,供学生课外阅读。这些书籍凝聚了众多数学家、数学教育家及数学教育工作者多年的心血,是值得每一个人用心去阅读的。对于学生而言,要完全理解这些内容是不现实的,但读书的乐趣、良好数学修养的形成、正确的数学思想方法和治学方法、尊重客观事实的态度及独立思考的习惯等,往往都蕴涵其中。随着时间的推移,随着知识的增加,随着阅历的丰富,学生会逐渐体会到其中的丰富内涵,这将让学生感到数学不再“面目可憎”,从而愿学、乐学,会学,并受益终生。
2.2 质疑
孔子日:“疑是思之始,学之端,”美国教育家布鲁巴克也指出:“最精湛的教学艺术,遵循的最高准则是让学生自己提出问题。”因此鼓励学生质疑、培养学生提问,是培养学生学会学习的重要途径。
“学贵有疑”,培养学生质疑提问的意识,首先应给学生营造一个宽松、民主、和谐的学习气氛;其次根据具体的内容,诱导学生通过观察、类比、猜想,提出概括性、置疑性、探究性或猜想性的问题,并鼓励学生去大胆地解决。另一方面,教师要善待学生提出的每个问题,能提出问题说明学生认真思考了问题。
比如在“集合”的教学中,学生对“空集”的有关问题提出质疑,为什么要“把不含任何元素的集合叫做空集”?这是我始料未及的。此时若简单地用“这是规定”来解释,实际上就是一种搪塞,学生是决不会满意的,也失去了一次发展学生思维的良机。因此我放手让学生去争论,并在争论中给予启发、提示。结果,学生联想到许多有关问题。本来用幂的定义看“![]() ”,它们简直“不是个东西”,但规定了它们的含义后,指数运算法则就适用于更大的范围,数学理论变得更加顺畅、和谐和系统。基于此,空集的有关规定才能被学生所接受和理解。同样的情况也出现于“平面向量”的教学中,“为什么要规定零向量?为什么要规定零向量与任一向量平行?”在后继的学习中,对于“直线的倾斜角”和“直线与平面所成的角”等也有类似的讨论。
”,它们简直“不是个东西”,但规定了它们的含义后,指数运算法则就适用于更大的范围,数学理论变得更加顺畅、和谐和系统。基于此,空集的有关规定才能被学生所接受和理解。同样的情况也出现于“平面向量”的教学中,“为什么要规定零向量?为什么要规定零向量与任一向量平行?”在后继的学习中,对于“直线的倾斜角”和“直线与平面所成的角”等也有类似的讨论。
再如,在“椭圆”的教学中,学生开始就不同意用比值“![]() ”、而执意主张用“
”、而执意主张用“![]() ”作为“离心率”来刻画椭圆的扁平程度,并振振有辞地说:“b、a分别是椭圆的短半轴和长半轴的长,用它们的比值来刻画椭圆的扁平程度多么直观形象!”此时,我没有急于将自己(即课本)的意志强加给学生,而是让他们在以后的学习中慢慢去领悟。在学习了整个“圆锥曲线”后,我发现学生们不但自然接受了为什么要如此定义离心率,还深刻地理解和掌握了这个定义的意蕴。
”作为“离心率”来刻画椭圆的扁平程度,并振振有辞地说:“b、a分别是椭圆的短半轴和长半轴的长,用它们的比值来刻画椭圆的扁平程度多么直观形象!”此时,我没有急于将自己(即课本)的意志强加给学生,而是让他们在以后的学习中慢慢去领悟。在学习了整个“圆锥曲线”后,我发现学生们不但自然接受了为什么要如此定义离心率,还深刻地理解和掌握了这个定义的意蕴。
2.3 探究
学生的学习过程是一个永无止境的探究过程。《新课标》指出:“教学中,既要有教师的讲授和指导,也要有学生的自主探究与合作交流。教师要创设适当的问题情境,鼓励学生发现数学的规律和问题解决的途径,使他们经历知识形成的过程,”因此,根据学习内容,结合学生的知识水平,创设有利于学生进行探究研讨的问题情境,把教材中阐述的内容创造性地,组织成生动有趣的、有利于学生探究发现的研究材料,让学生从中自主掌握有关知识与技能,体验科学探究的乐趣,学习科学探究的方法,领悟科学的思想和精神,对于培养学生学会学习是至关重要的。
比如,对数函数是运用所学函数知识去加以研究的一个重要初等函数,而对数的运算法则是学习对数函数、研究对数函数性质的基础和工具,因而是教学中的重点,同时也是一个难点。在实践过程中,我有意识地把“对数的运算法则”设计为探究性课题,搞了一次“数学实验”,让学生4人一组,利用计算器,自定M,N的值,自主探究![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 等之间的关系,并要求每一个小组选出一名组长,请他在探究结束后代表小组做汇报发言,向大家介绍小组的探究历程、交流实验心得、证明数学猜想。实践结果表明,学生们在“数学实验”中不仅兴趣高涨,而且通过计算、观察、归纳,发现了对数的运算性质,体验了数学发现、创造的历程,发展了创新意识,不仅认知结构得到发展,而且身心和品质也得到发展。正如他们自己所说:要“细心、严谨、耐心求真,勇于猜想,敢于实验。”、“通过自己的思考与实践所获得的知识更有趣,也更牢固。凡事都应认真对待,不能人云亦云,要自己探究个明白才能下结论。”
等之间的关系,并要求每一个小组选出一名组长,请他在探究结束后代表小组做汇报发言,向大家介绍小组的探究历程、交流实验心得、证明数学猜想。实践结果表明,学生们在“数学实验”中不仅兴趣高涨,而且通过计算、观察、归纳,发现了对数的运算性质,体验了数学发现、创造的历程,发展了创新意识,不仅认知结构得到发展,而且身心和品质也得到发展。正如他们自己所说:要“细心、严谨、耐心求真,勇于猜想,敢于实验。”、“通过自己的思考与实践所获得的知识更有趣,也更牢固。凡事都应认真对待,不能人云亦云,要自己探究个明白才能下结论。”
2.4 实践
《新课标》“倡导积极主动、勇于探索的学习方式”,要求“教学应力求使学生体验数学在解决实际问题中的作用、数学与日常生活及其他学科的联系,促进学生逐步形成和发展数学应用意识,提高实践能力。”因此,教学中注意挖掘数学知识的现实背景,再现数学的抽象过程,引导学生从数学的角度思考、提出、构造问题,鼓励学生去猜想、实践,学会主动寻求解决问题的方法,将探究性学习向课外延伸,这样做对激发学生的潜能、发展学生创造力、培养学生的应用意识和促进学生学习方式的转变是非常重要的。
比如在学习用基本不等式求最值时,我设计了这样一道研究性学习课题:调查市场上各种易拉罐的形状,并用数学知识说明设计的合理性。课题以课外作业的形式给出,要求在下一节课上交流研究成果并展开讨论。
设计这一研究课题主要基于:(l)易拉罐的形状及大小贴近学生生活实际,很容易引起学生的兴趣。(2)学生有能力自己去探究这一研究课题要解决什么问题,采用什么方法?学生通过对易拉罐的观察和测量得出如下结果:①易拉罐形状都是圆柱形;②易拉罐的高与直径之比大约是![]() 。提出了如下问题:a.厂方应怎样设计易拉罐,才能使用料最省?b.圆柱形的易拉罐当体积一定时什么时候用料最省?c.厂方为什么要将易拉罐的高与直径之比设计成
。提出了如下问题:a.厂方应怎样设计易拉罐,才能使用料最省?b.圆柱形的易拉罐当体积一定时什么时候用料最省?c.厂方为什么要将易拉罐的高与直径之比设计成![]() 等等。(3)由于问题具有开放性,因此有利于学生创新精神和实践能力的培养。
等等。(3)由于问题具有开放性,因此有利于学生创新精神和实践能力的培养。
对于问题a,学生都能答出当体积一定时,圆柱体比其它柱体用材省。对于问题b,学生通过计算得出:应设计成等边圆柱时用料才最省,可实际设计是易拉灌高与直径之比为 ,为什么要这样设计呢?对此问题展开讨论时,有的学生认为这是为了包装美观;有的学生认为易拉罐的底部会受到液体压强的作用,底部加厚些才不至于变形,……众说纷纭。这时我请同学们把易拉罐剪开再测量,学生测出壁与底部的厚度之比约是![]() ,然后请同学们用数学知识来验证设计的合理性。
,然后请同学们用数学知识来验证设计的合理性。
设罐壁造价为每平方单位a元,圆柱底面半径为r,高为h,体积为v,由于壁与底的厚度之比为![]() ,故罐底造价为每平方单位2a元。又
,故罐底造价为每平方单位2a元。又![]() ,从而
,从而
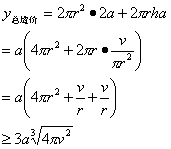
当且仅当![]() ,即
,即![]() 时造价最省。学生用自己所学的数学知识解决了实际问题。学生在探究实践中既巩固了所学知识,发展了创新意识,又提高了对数学价值的认识,培养了自身的数学应用意识。
时造价最省。学生用自己所学的数学知识解决了实际问题。学生在探究实践中既巩固了所学知识,发展了创新意识,又提高了对数学价值的认识,培养了自身的数学应用意识。
2.5 反思
所谓反思,就是从一个新的角度,多层次、多角度地对问题及解决问题的思维过程进行全面的考察、分析和思考。《新课标》指出:“人们在学习数学和运用数学解决问题倫敦銅时,不断地经历直观感知,……反思与建构等思维过程,这些过程是数学思维能力的具体体现,有助于学生对客观事物中蕴涵的数学模式进行思考和做出判断。”同时提出,评价应关注学生“能否不断反思自己的数学学习过程,并改进学习方法。”荷兰著名数学家弗赖登塔尔曾指出,“反思是数学思维活动的核心和动力”,“通过反思才能使现实世界数学化。”著名数学教育家波利亚也说,“如果没有了反思,他们就错过了解题的一次重要而有效益的方面。”通过反思,可以深化对问题的理解,优化思维过程,揭示问题本质,探索一般规律;通过反思,可以沟通知识间的相互联系,从而促进知识的同化和迁移,产生新的发现。因此,反思是一种积极的思维活动,在教学中引导学生学会积极的反思,对于培养学生学会学习是非常重要的。
比如在平时教学中,我要求学生从以下四个方面培养自己的数学反思能力,收到了较好的效果。
(1)建立学习档案。给自己建立学习档案,是养成良好反思习惯的途径。学习档案内容可丰富多样,如自己设定的学习目标,好的习题解法或学习方法,容易解错的习题,学习失败的教训等。
(2)听课反思。没有反思的听课是被动的、肤浅的。反思老师讲解,从中学习思考问题的方法,学会捕捉引起反思的问题或提出具有反思性的见解。如对于极坐标系这节课,反思应主要集中在为什么要引入极坐标系、极坐标系与直角坐标系的特点有何不同,以求顺利掌握极坐标系处理问题的方法。
(3)解题反思。问题解答后对结论的正确性进行检验或提出疑问;是否还有其他解法或更佳解法;能否对问题的题设或结论进行变式;能否把当前的命题推广到一般情况;进一步考虑问题题设的完备性(充分性)及结论的精确性等。
(4)写数学周记。反思是一种习惯和意识,不断地反思,才会不断进步。课堂上教师示范解题的过程中学生自己想到但未与教师交流的问题;作业中对某些习题不同解法的探讨;学习情感、体验的感受等,都可以通过写数学周记(或数学日记)的形式宣泄出来、记录下来,它使师生之间有了一个互相了解、交流的固定桥梁。
以上仅是本人多年教学中的一些粗浅体会。按照新课程标准的要求,转变学生的数学学习方式,是一项长期且艰巨的工作,但我坚信,只要我们从小处人手,从一点一滴抓起,必将有利于学生数学素质的不断提高,有利于确保新课程改革的顺利进行。
参考文献:
1.中华人民共和国教育部制订.普通高中数学课程标准(实验).人民教育出版社,2003.4
2.钟启泉.基础教育课程纲要(试行)解读.教育科学出版社,2001
3.曹一鸣.略论数学反思能力的培养.中学数学教学参考,2004.9
4.曹勇兵.研究性学习的实施策略与实践.教育实践与研究,2004.2