利用TI图形计算器改进高中数学的教学方式

关键词 TI图形计算器　改进　知识的形成过程

一、TI图形计算器的使用为改进数学教与学创造了条件

（一）教学思考

在当前中学数学教学中，探索进行创新教育和实践活动的途径与方法，深化教学改革，是我们广大数学教育工作者的紧要任务．

使用现代化信息技术辅助教学，如计算机、TI图形计算器、网络技术等是促进教育改革、实施创新教育的有力工具，我们开展TI图形计算器在中学数学教育中的研究课题，已经对教师的教育观念和学生数学知识的形成甚至于在改变其学习方式等方面都产生了很大的影响．

TI图形计算器功能强大，应用很广泛．比如：它的几何作图系统，不但能作教学中我们碰到的几乎所有的函数图象及方程曲线，还能进行动态演示，以及图形的变换，进行数与形结合的分析；而它的代数运算系统，能进行数式计算和方程的求解，也能解决复杂的数据处理等．

例如：线段的定比分点的坐标表示教学

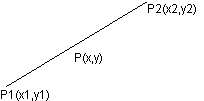
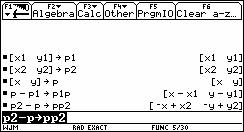
 图1 　　　　　　　　　　　　　　　　　　 图2

如图1线段P₁P₂上有一点P，设P₁(x₁，y₁)，P₂(x₂，y₂)，P(x，y)，设p分有向线段所成的比是，那么用向量表示就是，在图形计算器上可以求出x，y的结果来．用键盘直接输入[x₁，y₁]到P₁中，[x₂，y₂]到P₂中，[x，y]到P中．然后再计算P₁-P并转换成向量PP₁，计算P₂-P转换成向量PP₂，如图2所示，(TI?92图形计算器把点的坐标看成是该点对应的向径的坐标，因而直接用向量来表示点)．

再直接输入P₁P=t*PP₂(如图3)，显示出来一组方程组的表达式．那么我们要求解的是P点的坐标x，y，这也可以通过TI-92自动完成．

图3

按F2和1得到solve，解出定比分点坐标公式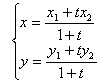

TI?92的代数系统，使得我们可以对代数，即变元进行计算，这样我们不仅可以计算数字，同时也可以就一般情况进行分析．如上例，利用图形计算器计算定比分点的坐标，可以帮助学生更好地理解向量的代数特征，向量的坐标表示以及向量的代数形式对于问题解决的重要性．

另外，TI图形计算器还可以为我们教学中进行象“观察──探究──发现──猜想──验证”这样的活动提供了强有力的支持，这有利于教师创设适当的情景来引导学生主动探究、再创造和建构知识，因此改变了学生的数学知识的形成过程，可以说，手持教育技术为我们提供创设了主动式学习的平台．

（二）使用TI图形计算器影响学生的数学知识的形成

首先是使用TI有利于激发学生的学习兴趣和欲望，心理学告诉我们：“兴趣是人们对事物的选择性态度，是积极认识某种事物或参加某种活动的心理倾向．它是学生积极获取知识形成技能的重要动力．” 兴趣之根本在于它是使得学生知识的形成是主动式的，而非传统的被动式形成．

其次是使用TI图形计算器更能直观、形象、动态的展示知识的形成过程 ，《教学大纲》明确指出：“在教学中，应当注意数学概念、公式、定理、法则的提出过程，知识的形成、发展过程，解题思路的探索过程，解题方法和规律的概括过程，使学生在这些过程中展开思维，从而发展他们的能力．” 我们把TI图形计算器应用于数学教学过程中，正好利于揭示数学概念、公式、定理、法则的形成过程，在解决某些数学问题时，有利于启迪学生的思维，让学生去寻找解决问题的途径和方法．

例如：学习函数y=Asin（ωx十φ）的图象．

研究该函数的图象，需要揭示A、ω、φ三个量的取值对该函数图象位置的影响，同时要揭示函数y=sinx, y=sinωx, y=Asinωx， y=sin(ωx+φ)等不同函数之间的图象变换关系，这就要给A、ω、φ各个不同的取值，作出其图象，让学生进行比较，在教学中我们利用TI图形计算器，作出各种不同的图象后，让学生自己通过观察、分斩、比较得出结论．实践证明，学生自己揭示出知识的形成过程，不但提高学生的直觉思维、形象思维能力，而且提高了学生的抽象概括能力，同时，让学生在获取知识时，也获得了获取知识的思维途径和方法．

二、TI图形计算器对于改进形成数学知识的的教学案例

反思以往的教学工作，有时觉得难免会存在着重结论、轻过程的教学倾向，这种倾向严重的影响到学生的数学知识的形成过程，它的产生虽然有客观原因，但结果是我们对数学知识的教与学，常回答的只是“是什么”，而对“为什么”缺乏阐述，对结论是怎么产生的，产生这个结论的数学思维途径、思维过程、思维方法也往往被忽视，这就限制了学生的数学思维水平的提高．而从某种意义上，学生获取了获取知识的思维方法比知道的一些知识更为重要，因此把TI图形计算器应用于教学活动中，笔者时刻注意让它有利于改进数学知识形成过程的教学．下面是两个教学中的案例：

案例1 §5.2向量的加法与减法习题课教学片段

例题：(摘自普通高级中学实验教科书（信息技术整合本）数学 第一册（下） 人民教育出版社)

已知O为四边形ABCD所在平面上的一点，且向量、、 、满足等式=．

试用图形计算器或计算机作图，观察四边形ABCD，你能发现什么规律？试用向量方法证明你所发现的规律．

本题考查学生掌握向量的运算方法的能力及对向量的几何特性的认识，如果不使用TI图形计算器，那么只是将已知向量等式=，结合向量减法的意义考虑把它变形为。由此可知四边形是平行四边形．这种解法对于学生数学知识的形成的过程并不起多大的作用，只能算是一种逻辑推理的强化练习．

然而，用TI-92作图，用数学实验的方法，让学生真正看到向量这种既有大小又有方向的量的在相加过程中的变化情况，自己追踪整个改变的过程，那么对向量加法这一知识的认知就不再停留在公式化的层面上了，学生从图中发现了当向量与不等时，四边形不是平行四边形（如图4），当与相等时，四边形是平行四边形（如图5）．

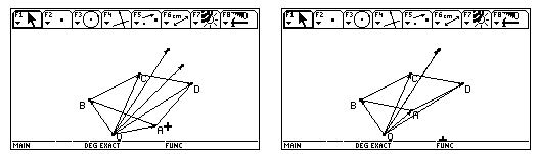
　　 图4 　　　　　　　　　　　　　　　 图5

信息技术整合本教材中不是生硬地要求学生证明结论，而是先让学生能借助于技术进行活动，通过活动让学生发现规律得出结论， 这样学习活动不只是接受、记忆、模仿和练习，学习过程成为在课程引导下的“再创造”过程，学生体验了数学发现和创造的历程，这样的学习不仅让学生获取知识，同样也有利于学生的知识迁移，发展学生的创新意识与创造能力，当然，最后在实际教学中学生受到TI图形计算器显示结果的启发，都顺利的证明出了四边形 是平行四边形的结果，教学收到了良好的效果．

案例2 §7.4 简单的线性规划

问题:某公司从应届毕业生中招聘工作人员，打算本科生与专科生共招聘20人到50人，其中本科生不小于专科生的一半，且本科生至少12人，试用期本科生月工资每人900元，专科生月工资每人600元．在这样的条件下，从老板的角度考虑，怎样招聘才能使月工资总数最少？

[分析]在教学中通过此例，可让学生了解线性规划的概念、基本步骤和原理,在此学习过程中，由于借助TI图形计算器，它不仅使常规数学应用问题中让人感到困难的数据处理问题，变得省时、方便、直观和形象，它还可以科学地强化信息传递的结果，激发学生学习、探究线性规划问题的兴趣，从而激发学生浓烈的探索欲望，增强课堂的求知气氛，让此知识的形成过程达到最优化．

解：设招聘本科生x人，专科生y人，则：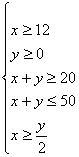

设公司老板花费为k元，k=900x+600y，欲求k的最值．

①利用图形计算器找出约束条件（如图6），定出目标函数；

②找出约束条件的解的集合的图形,运行程序，动态观察目标函数；

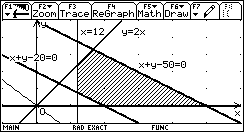
图6

③观察目标函数的取值随着直线的平移而变化的情况，在动画演示过程中学生自己找到

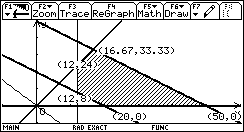
图7

了最大值和最小值（如下图7）．最后得出结论

答：招聘12个本科生，8个专科生时，花费最小，为15600元．

审视上述学生获取线性规划知识的过程，TI图形计算器的程序功能在此发挥了技术优势的作用，它的直观不仅是使学生看到了动态的图像，理解了找最优解的关键，而更重要的是学生在这一学习过程是自始至终的、完整的主动参与与延续性学习的过程，这极大的丰富着每一个学生的数学知识形成的体验，这些将成为他们日后获取新知的源泉．