对“正弦函数的图象”的探究课例

主题词 TI图形计算器 实验 探究

函数y=Asin()与y=sinx的图象的关系，参数A、、 对y=Asin（ x+ ）图象的影响，学生较难抽象，老师用传统的方法难以帮助学生理解，因此，本节知识借助TI图形计算器采用实验探究法能很好地实现教学目标：

（1） 认识对函数y=Asin()图象的影响．

（2） 理解图象变换的本质．

（3） 掌握主要的两种图象变换方法．

（4） 培养学生积极探究的学习品质．

（5） 使学生能结合具体函数图象的变化，领会由简单到复杂，特殊到一般的化归的数学思想．

教学情景

一．课题导入：

比较函数式y=Asin()与y=sinx，发现前式增加了三个参数．当A=1， =1，取 =0时就为y=sinx，当A=1， =1，取 = 时就为y=cosx，正弦、余弦函数是函数y=Asin( 的特殊情形．所以引发了学生很想知道该函数图象与正弦曲线的关系和A、 、 是怎样影响函数y=Asin( x+ ),x的图象的？

二．实验探究过程：

在此过程中，学生用“TI图形计算器”画函数图象．

把学生分成三个组，要求三个组分别对A、 、 赋不同的值，探索图象规律．

实验要求：改变一个参数值，与的图象作比较，思考变化的本质并说出你得到的结论．

实验：

（一）函数与的关系，常数使函数的图象发生怎样的变化？

学生用图形计算器对赋不同的值画图，观察图象变化的规律．如：函数的图象1、2．

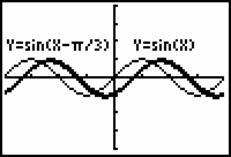
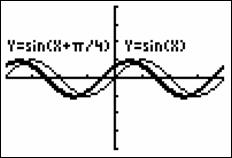
图1 　　　　　　　　　　　　　　　　 图2

它们的图象分别向右、左平移了，为什么？这时学生讨论很热烈，通过对比图象发现，当时， 即，，故要得到函数的图象只需将的图象向右平移个单位，类似要得到的图象也只需将的图象向左平移个单位．离开技术支持的教学，学生很难达到快速理解其中的道理，都是机械地记住教师教给的“死”办法，“左加右减”，在运用环节上大多数学生就会出问题了．

（二）函数与的关系，常数使函数的图象发生怎样的变化？

　学生用图形计算器对赋不同的值画图，观察图象变化的规律．

如：函数 y=sin2x， y=sinx”的图象3、4．

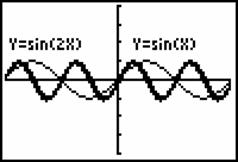
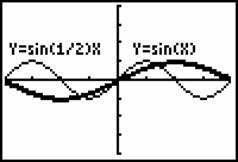
图3 　　　　　　　　　　　　　　　　　　 图4

函数比图象变化的频率加快，为函数周期的倍，为什么？学生通过思考，分析发现的现象，寻找变化的本质，当，即时，，故要得到的图象只需将图象上各点的横坐标缩为原来的倍，纵坐标不变．此时，学生不但会观察图象，也摸索出分析图象的规律．他们很快就回答出要得到的图象，只需将图象上各点的横坐标伸长为原来的2倍，纵坐标不变．

（三）函数与的关系，常数使函数的图象发生怎样的变化？

画函数的图象，如图5、6．

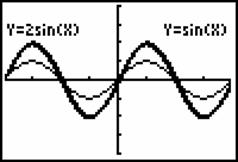
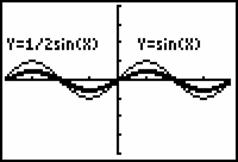
图5 　　　　　　　　　　　　　　　　　 图6

观察学生的学习表现，看出他们已能由对比函数式到图象，发现对同一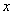值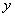，值分别是原来的2倍和倍，故要得到的图象，只需将的图象上各点的纵坐标分别伸长、缩短为原来的2倍，倍，横坐标不变．

在此过程中，学生通过画图，观察、分析、推理，已理解了参数A、 、 对函数图象的影响，每个小组的学生都能正确陈述自己所观察到的结论，而且说得很完整．归纳结论如下：

1． 值使图象相对的图象向左或向右平移了个单位, 这种图象变换称为相位变化，它是图象的平移变换．

2． 值使图象上每一点的纵坐标不变，横坐标变为原来的倍，我们把它称为图象的周期变化，它是图象的伸缩变换．

3． 值使图象上每一点的横坐标不变，纵坐标变为原来的倍，改变了函数的最大和最小值，我们把它称为图象的振幅变化，它也是图象的伸缩变换．

TI图形计算器为学生提供了直观的感受，图象之间的变换关系深刻地印在了他们的脑海里．

三．运用过程

弄清上述变化规律后，把三个参数对图象的影响连贯起来．

问：我们如何通过图象的变换由一个函数的图象得到另一个函数的图象．

（一）由的图象分别得到，，的图象？

学生由前面的学习很快得出结论如下：

1．要得到函数的图象，只需将的图象上所有点向左或向右平移个单位．

2．要得到函数的图象，只需将的图象上所有点的横坐标伸长或缩短到原来的倍，纵坐标不变．

3．要得到函数的图象，只需将的图象上所有点的纵坐标伸长或缩短到原来的倍，横坐标不变．

（二）由的图象得到的图象你有哪些变换途径？

以“…… ”为例探讨．

学生说出了六种变换途径，具体的变换过程如下： 的图象变换途径：

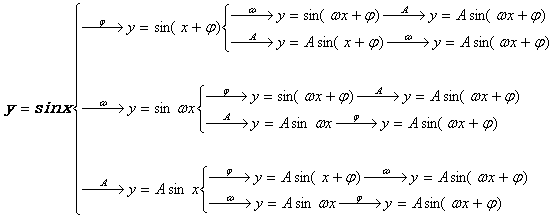
学生虽然找到了多种变换途径，但在具体操作过程中，在先生成后生成或先生成后生成上平移量的多少认识不清，我观察到他们书写时几乎都是向左平移，提问学生对吗？启发学生在图形计算器上分别画出和的图象，如图7、8所示，进行比较，学生发现它们平移的单位是不一样的，前者向左平移了个单位，后者向左平移了个单位，原因何在？这时，有一位学生举手，说出，，结论就是图形计算器上显示的结果．由图形计算器成形，引发了学生的好奇心，激发了学生去求真的欲望，培养了学生科学的认知态度．

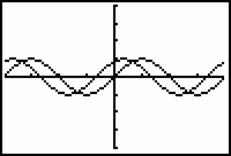
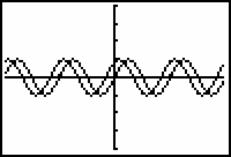
图7 　　　　　　　　　　　　　　　　　 图8

让学生归纳得出主要的两种变换顺序的具体过程：

先伸缩后平移：

先平移后伸缩：

四．学后反思

（一）当你能处理吗？

（二）这种图象变换方法还可以推广到其它各三角函数和一般函数吗？

如，，，图象间的变换．

学生的探索欲望非常强烈，学生课下的学习已有了方向，这节课为学生探求一般函数的图形变换规律作了一个铺垫，它的深刻意义在于，教师教的目的在于不教，培养学生的自主学习能力．

TI图形计算器的运用，使数学实验进入课堂，从这节课中我们可以看到，学生通过动手操作，不断改变参数值，观察并记录图像的变化特点，得到初步体验后讨论分析参数对函数图像的影响，借助直观的活动实现和揭示其知识的内在联系，充分调动了学生的学习积极性，教师的指导和学生的主观能动性得到更好的发挥．本节课使用了展示平台，学生在TI图形计算器上的探索过程展示在大屏幕上，很好地呈现了他们的学习结果，较好地把技术与数学学习的本质结合起来，培养了学生的成就感，达到了很好的教学效果．

参考文献

人民教育出版社中学数学室：《普通高级中学实验教科书（信息技术整合本）数学第一册（下）》， 2002年12月第一版，P．60

孔企平 张维忠 黄荣金：《数学新课程与数学学习》，高等教育出版社．