利用手持技术转变学生的数学学习方式

主题词 TI手持技术 学习方式

随着现代教育技术的发展，多媒体技术逐步应用到了教学领域，多媒体技术集图、文、声、像、动画于一体，促进了教学方式的重大变革．TI手持技术的日益成熟，也为学生的学习方式带来了相应的变化．在这一变革下，教师应怎样来教？学生应怎样来学？是摆在我们数学教育工作者面前，迫切需要解决的问题．

课程改革明确提出：要充分发挥学生的主观能动作用，自主学习，主动探究，培养具有创新精神的学习者．为此，学生学习方法的改变显得尤其重要．一位教育专家说过这样一个故事：中国一位小学生到美国参加夏令营活动，他同一位刚认识的美国小学生在一起交谈，他得意地问对方：你知道什么是“算盘”吗？美国小学生一愣，说：“不知道，不过请等一下”．随后他快速坐到电脑旁，打开电脑，进入互联网，不一会儿，拿着刚打印出来的他在网络上查阅到的大量有关“算盘”的资料到中国小学生面前说：“我现在知道了．”于是他手拿资料，向中国小学生介绍了有关“算盘”的起源、发展、功能等，直听得中国小学生一愣一愣的，许多知识都是他从未听过的．两种不同的学习方式，中国小学生是在课堂上听老师讲授来学习知识，而美国小学生是利用现代信息技术──互联网来学习知识．一种是传统学习方式，一种是现代的学习方式，两种不同的学习方式，孰优孰劣，读者自己不难分辨．教育的目不仅仅是使学生掌握知识，还应该是教会学生怎样去获取知识，掌握学习的方式，而不在于教师能“灌”多少知识．

我校2002年首次使用TI实验学校教材，经过三年的使用，感触颇多，无论是从教师的教学方式，还是学生的学习方式，都较以往都有了很大的不同．这里我主要谈一下学生在TI图形计算器介入下怎样去适应学习方式的变化，应注意哪些方面的问题．

首先，一定要解决好技术关．打个比方，若把学生看作猎人，知识看作猎物，那么TI图形计算器可看作是猎枪．对于一个新猎手来说，能否打到猎物，最重要的应该是先熟悉手中猎枪的用途用法．对学生而言即要求首先熟悉图形计算器的功能，它可以用来完成哪些工作，怎样操作？由于教学大纲中并未给出学习图形计算器所需课时，且它是全英文界面，其中有大量的英文单词或缩写．要想在短时间内掌握，学生只有在教师的帮助下才可能完成．当然，其中有些功能在高中阶段基本用不上，如微积分、矩阵计算、概率统计等可先不做要求，把重点放在函数和数组两个部分．要求能作出各种函数的图象（分段函数和散点图等）；会求图象的交点、最大值、最小值；会进行简单函数的图形拟合等，时间控制在两周以内．这样学生对图形计算器需掌握哪些功能比较明确时，可在较短时间内起到良好的效果．也只有在学生比较熟悉图形计算器的各功能之后，才能进行下一步的正常教学工作，所以我认为学生必须突破的第一关是技术关．

其次，要过好过程关．这里所说的过程是指获取知识的途径和方法．就象猎人仅只熟悉枪的功能和作用还不够，他还必须学会如何寻找瞄准猎物，扣动扳机，击中目标这一过程．前期工作学生已熟悉TI图形计算器的常用功能，下一步他急切地想知道这些功能到底能帮助自己解决一些什么问题？怎样去做？教师这个时候的引导非常重要，千万不可操之过急，应循序渐进地从实例出发，引导学生去观察、去发现，去归纳，去解决，最后形成自我解决问题的能力．建构主义数学论中明确指出：数学活动应当是从实际生活中的问题出发，学习者通过自主的参与、交流、发现，和原有的数学认知体系作用，最后合并成为新的数学结构体系，它是不可能从一个人迁移到另外一个人的．例如，在讲解二次不等式时，教师可设计如下过程：

教师：上述不等式可以利用图象来求解吗？

学生议论，有的说能，有的说不能，但都无法说明理由．

教师：大家仔细思考一下，我们学习过的什么知识能和“图象”联系在一起呢？

学生易知“函数”能和“图象”联系在一起．

教师：好，哪怎样才能把不等式和函数联系起来？（引导学生观察不等号左右两边的式子．）

学生：不等式左边是一个二次三项式，可考虑和二次函数y₁=联系在一起；而右边是常数零，可看作常值函数y₂= 0．于是可将y₁和y₂两个函数输入图形计算器，作出其图象并观察（如图1）．

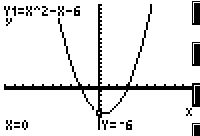
图1

学生：y₁是开口向上的抛物线，与x轴有两个交点，y₂是一条直线，正好与x轴重合，但仍然看不出解集．

教师此时可引导学生从函数解析式的意义入手，若要成立，即要 y₁> y₂成立，在图形中我们可找一下，看看x取哪些数值能够使上式成立？

学生：从图象上看（如图2），当x值取两个交点的外侧部分时，y₁的图象总在y₂的图象上方，此时有y₁> y₂成立．

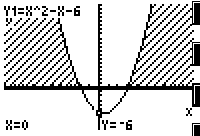
图2

于是问题转化为求出抛物线与x轴交点坐标，利用图形计算器中求图象交点的功能，学生很快算得x=-2或x=3．所以不等式的解集为：{x|x<-2或x>3}．

在教学中，对于引导、观察、探索和发现这一过程，教师应特别向学生强调注重“探究”的过程．因为这些学生都是在九年传统教学方式下训练出来的，课堂上思维活动量很小，并且很习惯这种被动式的学习方式，要想转化为主动式、探索式学习，在实际操作中有很大困难，所以教师一定要树立信心，坚持长抓不懈，并注意学生能完成的不要包办代替，要让学生在教师的帮助和引导下一步一步，踏踏实实地亲身去参与体会学习和研究问题的方法．教会学生听课的方法，注重学习教师在解决问题时的思考方式和思维过程，而不要把注意力过多地集中在数字的运算上．课后注意及时复习和小结，注重对知识的灵活运用．长此以往，学生在不断的积累中，将逐渐学会独立思考，自主探索和解决问题，真正做到会学，会用．这将对学生的终身学习有很大的帮助．要让学生意识到在学习过程中，掌握知识固然很重要，但更重要的是要掌握获取知识的途径和方法，这样即便“无师”也能“自通”．

最后，要注意探索结果的回归．数学是一门具有严密逻辑性的学科，讲究的是严谨的推理和论证．因此在国际上利用图形计算器直观得出的结果是不被认可的，而且目前在考场中图形计算器还不允许带入．所以学生应该明确，手持技术只是用来帮助学习和探索的工具，从图形计算器中得出的结论必须用数学的符号和文字来进行阐述和论证，这即是直观图形向数学逻辑的回归（或称转化）．例如这样一个题：

已知等差数列5，，，…，当项数n为多少时，S_n可取到最大值？学生从前3项很快可算出通项公式为a_n=和前n项和公式S_n=，利用TI图形计算器中的数组功能进行列表和作散点图（如图3），从表格和图中可看出n=7或n=8．

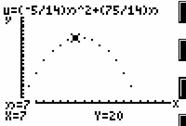
图3

以上是从图形直观得出的结果，还必须回到论证中来，以下给出证明：

∵a1=5＞0， d=＜0 ∴该数列为递减数列．要S_n最大,只须将所有的非负项相加即可．而非负项应满足a_n≥0, 即≥0, 解得n≤8.． 又∵当n=8时, a_n=0, ∴当n=7或n=8时, S_n有最大值．

以上解题模式为：问题的提出探究（借助信息技术）发现归纳推理 论证．整个过程充分体现了数学思维推理活动的特点，是符合认知发展规律的．

新技术所带来的新的教育模式、学习模式，改变了以往老师讲，学生学的方式．把以往枯燥的数学课变得生动、形象、直观，从而激发了学生的学习兴趣，调动了内因，增强了求知欲和学习的主动性，使学生能逐步养成良好的学习方式，有利于创新精神的培养．而这一切，都基于教育工作者必须要认真学习先进的教育理念，在现代教育思想的指导下，转变观念，起好教师的引领者、设计者的作用．