三角函数图象变换课例

主题词 三角变换 观察 动画演示

教学过程：

一、新课引入：

师：前面我们学习了正弦函数y=sinx的图象和性质，请同学说出它的定义域、值域、奇偶性、周期及单调区间？

生：定义域：R，值域：[-1，1]，奇函数，单增区间：[]单减区间：[]

师：回答的很好，那么形如函数的定义域、值域、奇偶性、周期及单调区间又如何呢？

（一片茫然，没有学生回答）

师：大家别着急，今天我们就要来学习它们的图象和性质，并通过它们的图象和性质进一步来探究它们的图象与y=sinx图象会有什么样的关系．

二、动手实验：

下面请大家用图形计算器在同一坐标系分别输入以下几组三角函数的图象，并观察每一组图象的定义域、值域、周期、单调区间及其再观察每一组图象相互之间的关系、特点，然后进行小组讨论、交流．

第一组：

第二组：

第三组：

（教师巡视，同时指导学生注意输入中经常出现的几个问题：窗口调节、弧度与度的单位转换、及其如何利用在同一坐标系同时画图和利用功能键进行追踪和如何利用其它键进行的放大等等．）

三、师生交流：

师：从下列第一组图1，你有什么体会？

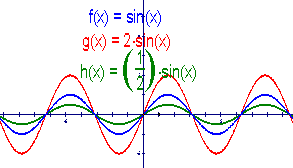
图1

师：的定义域、值域、周期分别是多少？

生：的定义域：x∈R，值域：y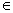［－2，2］，周期：应该与y=sinx的一样还是

师：不错，那么呢？

生：的定义域x∈R，值域：y∈［－，］，周期：

师：很好，那么它们三者之间的图象有什么关系呢？

生：好象它们之间有一定的伸缩关系

师：能不能再说得具体一点吗？

生：伸缩倍数是不是与2和有关呢？

师：大家探究和分析的很好，是不是这样呢？不过别着急．下面请大家先看大屏幕几何画板的动画演示

（老师心喜：他们能够说出“伸缩”二字，而且发现与2和有关，只是猜想不知是否正确，此时，利用动画演示有助于验证他们的猜想）

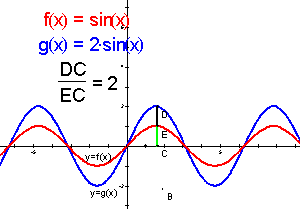
图2

演示1：拖动点C,请大家观察图象上D、E的运动，在横坐标相同的条件下，纵坐标的变化，同时注意比值的变化．（对比y=sinx与y=2sinx）

图3

演示2：拖动点B，观察图象y=sinx与y=Asinx图象，当A发生变化时，点D、E的纵坐标的变化，同时注意比值的变化．（改变A的值，整体对比y=sinx与y=Asinx的关系）

进一步引导,观察,启发：

师：通过上述大家的实验、和我刚才的几何画板演示，你又有什么体会？

生： 函数y=1/2sinx的图象可看作把y＝sinx，x∈R上所有点的纵坐标缩短到原来的 倍而得(横坐标不变)，函数y=2sinx图象可看作把y＝sinx，x∈R上所有点的纵坐标缩短到原来的2倍而得(横坐标不变)

师：太好了，回答完全正确．

（演示进一步巩固了他们的猜想）

教师总结：

一般地，y=Asinx，(x∈RA>0且A11)的图象可以看作把正弦曲线y=sinx上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的．我们把这种变换简称为振幅变换．

第二组：

师生交流：

师：和第一组一样，你们有什么体会？

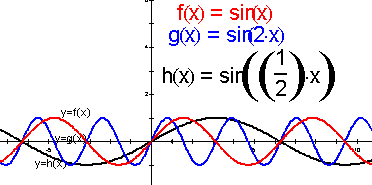
图4

师：与的定义域、值域、周期分别是多少？

生：与的定义域：R,值域：[-1，1]，和y=sinx的都一样，周期是多少看不出来，反正它们的周期显然不一样．

（学生从图形计算器屏幕看到的的确如此，它们的周期明显不一样）

师：是的，他们的图象差别太大，但是可以看出一个周期较小，一个较大．

（教师想通过周期的不一样来突破周期变换）

现在我给大家演示两个动画3．

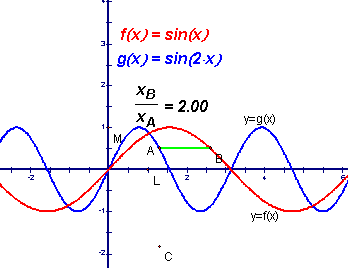
图5

演示1：拖动点A （A、B,它们分别在各自的图象上）在纵坐标相同的条件下，观察A、B的横坐标的变化，以及的比值的变化．（对比y=sinx与y=2sinx的关系）

演示2：拖动点B, 改变W的值，再观察上述的变化．（改变W的值，进一步观察y=sinx与y=sinWx的图象关系）

(该环节的演示要慢，要让学生注意观察比值的不变特点)

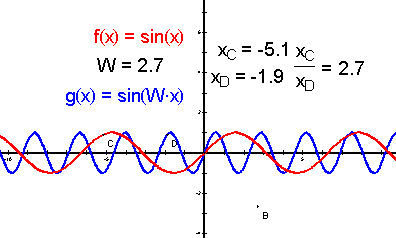
图6

进一步引导, 观察启发:

师：通过上述你的实验、和几何画板的动画演示，你又有什么体会？

生：函数y＝sin2x，x∈R的图象，可看作把y＝sinx，x∈R上所有点的横坐标缩短到原来的倍(纵坐标不变)而得到的 函数y＝sin，x∈R的图象，可看作把y＝sinx，x∈R上所有点的横坐标伸长到原来的2倍(纵坐标不变)而得到

（的确难得，他们能发现影响周期的量是W了，这样也为下一节课周期的教学作好准备）

师：大家已经能通过第一组的变换特点，类比的方式得到它们之间的关系，真的很不错．那么谁能把y=sinωx图象与y=sinx的图象作比较 ，说出它们之间的关系吗？

生：函数y=sinωx, x∈R (ω>0且ω11)的图象，可看作把y=sinx所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍（纵坐标不变）

（鼓励学生用自己的语言来归纳，总结）

师：有进步．

总结：

一般地，函数y=sinωx, x∈R (ω>0且ω11)的图象，可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍（纵坐标不变）．我们把这种变换简称为周期（或者伸缩）变换．

第三组：

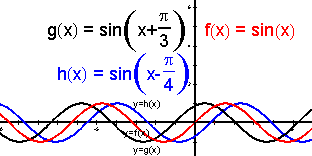
图7

师：它们的定义域、值域、周期分别是多少？以及它们的图象关系又有如何关系？

生：定义域：x∈R，值域：y ∈［-1，1］，周期：，图象似乎与我们以前学过的具有平移关系．

（因为高一学习过一些简单的平移，学生对平移的说法可以很快的提出）

师：回答的十分正确．那么大家再用功能键追踪，观察它们的平移的方向和平移的单位有什么特点？

（由于学生的图形计算器的单位是幅度，追踪的结果是一个数，不会带有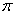的单位，让学生注意进行换算，几分钟后）

师：请大家看我用几何画板的动画演示4．

演示1：拖动点C,观察变化．（观察平移的单位）

演示2：拖动点B,改变B的值，观察平移的方向．（让学生去发现：从左边移动(B>0)，从右边移动（B<0）

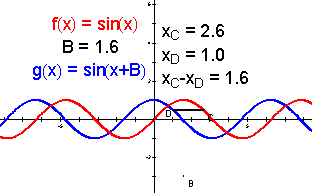
图8

引导,观察,启发：

师：通过上述实验、和几何画板演示的结果你有什么体会？

生：函数y＝sin(x＋)，x∈R的图象可看作把正弦曲线y=sinx上所有的点向左平行移动个单位长度而得到 .函数y＝sin(x－)，x∈R的图象可看作把正弦曲线y=sinx上所有点向右平行移动个单位长度而得到

师：太棒了，回答的十分正确．

教师总结：

一般地，函数y＝sin(x＋)，x∈R(其中≠0)的图象，可以看作把正弦曲线上所有点向左(当＞0时)或向右(当＜0时＝平行移动｜｜个单位长度而得到 (用平移法注意讲清方向：“加左”“减右”)，我们把这一变换称为平移变换

四、运用反思：

1、下列变换中，正确的是

A 将y＝sin2x图象上的横坐标变为原来的2倍(纵坐标不变)即可得到y＝sinx的图象

B 将y＝sin2x图象上的横坐标变为原来的倍(纵坐标不变)即可得到y＝sinx的图象

C 将y＝－sin2x图象上的横坐标变为原来的倍,纵坐标变为原来的相反数,即得到y＝sinx的图象

D 将y＝－3sin2x图象上的横坐标缩小一倍，纵坐标扩大到原来的倍，且变为相反数，即得到y＝sinx的图象

答案：A

（可以让学生使用机器来验证自己的回答是否正确，尤其是C和D的回答）

2．

师：大家可以选择变换路径

（由于前面都是单一的变换，可以提示学生先选择变换路径）

生： 即把y=sinx图象上所有点的横坐标不变，纵坐标伸长为原来的2倍，再把得到的图象的纵坐标不变，横坐标缩短为繁体字原来的1/2，然后把图象上的所有点向右移动个单位．

师：有不同意见吗？

生：是的，基本就是这样．

师：从一定是向右平移个单位吗？

生：是啊

（全体学生感到纳闷，老师为什么这样问呢．）

师：好吧，请大家用计算器实验，看看他说的是否正确？

生：我输入图象看，平移的数据似乎不对，到底是多少呢？

（由于学生的图形计算器的单位是幅度，追踪的结果是一个数，不会带有 的单位，可以让学生进行换算来回答，但是几何画板可以动态变化和计算）

师：请大家再看我的演示：拖动点A,观察点A、C横坐标的变化．（观察它们距离的单位刻度是多少．）

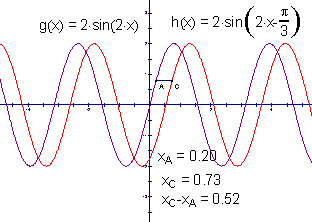
图9

生：我知道了，应该是向右平移，而不是

师：不错应该是应该是向右平移，这是我们经常会犯的错误，一般地，函数的平移是指变量的变化量，所以要把函数化为从中可以看出，所以应该是向右平移

（这时学生在做次类题目，经常容易犯的错误，应引起足够的重视）

五、小结与思考：

今天我们学习了三种三角函数：形如图象是由y=sinx的图象怎么变换得到，我们分别把三种变换分别称为振幅变换、伸缩变换、平移变换．

思考：

上述三种三角变换适应于三角函数的图象外，是否也适应于一般函数的图象的变换吗？请同学们下去通过今天学习的方法用图形计算器探索、思考下列几组函数图象的关系

1、与

2、

3、

（让学生下去动手实践，、探索和验证，也为后期函数图象变换的学习作准备）

六、作业：

七、教学反思：

1、本节课是以学生探索为主，教师点拨、启发、引导和利用几何画板的演示为辅．通过TI-92PLS图形计算器进行教学学习和探究活动，获得TI计算器正弦波函数性质等数学问题的体验；认识现代信息技术对学习数学知识和探究数学问题的价值．借助已知知识提出问题，体现教师为主导，学生为主体的原则，整个教学过程为：提出问题探索解决问题运用反思提高．

2、以前该部分内容的教学通常是通过取值、列表、描点、画图然后静态的让学生观察、总结，最后得出它们之间图象变化的特点，如下图所示．

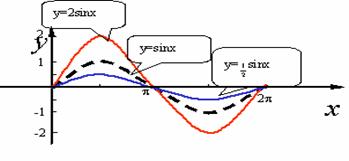
（振幅变换）

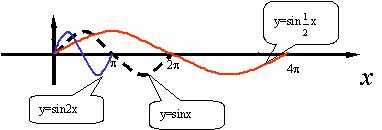
（周期变换）

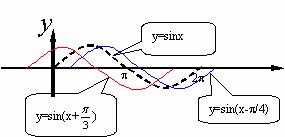
（平移变换）

不仅教学内容少，而且课时需要多（以前至少需要2课时）、课堂气氛枯燥、学生参与的活动少、学习的积极性较低．通过信息技术的使用，改变常规教学中处理方式，利用图形计算器让学生实验、观察、体会和交流，然后再通过几何画板的辅助教学演示，使得振幅变换、伸缩变换、平移变换变得形象、直观，学生易于理解和掌握，不仅一节课完成了三种变换而且学生的兴趣浓厚、参与活动多、课堂气氛活跃，使课堂教学落到了实处，主体作用得到了真正的体现，综合能力和素质也得到了培养，这充分体现了信息技术具有的优势．

3、但值得商榷的是：原来教学的“五点作图法”绘制函数图象，再讨论参数所起的作用，这里用技术马上就画出函数图象，并观察规律得出结论，所以“五点作图法”在技术面前如何处理会更好．