应用图形计算器学习函数注意“想、作、思”结合

主题词 图形计算器 函数图象 渐近线 操作 思考

普通高级中学实验教科书（信息技术整合本 数学）第二章《函数》是学生使用信息技术帮助数学学习较充分的一章，特别是图形计算器画函数图象的功能、列表的表达方式，极大地拓展了师生教与学的空间，学生的自主探究性学习较易实现。但在现实教学中，我们的良好愿望在多大程度上能够实现，实践中应注意哪些问题，下面以亲身经历的两件事谈一谈应用图形计算器学习函数学生应注意的问题。

案例一 渐近线

在一次测验中，为了考查学生对基本函数图象的掌握情况，设置了一个画函数图象简图的题目，其中一个函数是（测验时不允许使用图形计算器），让我感到奇怪的是实验班（使用信息技术整合本 《 数学》并配有图形计算器的班级）的部分同学“画蛇添足”，在y轴负半轴的某个位置画了一个空心点，从这个点引出一条上升的曲线，而非实验班的同学却没有这样画的。为什么呢？我找来出现此种错误的学生询问，他们指着图形计算器上的图象说：“上面就是这样画的，考虑到对数的真数不能为0，而没有定义的点应当是空心点，就想当然地这样画了。”我回忆在两个班（一个实验班，一个非实验班）的教学中对函数图象的处理情况，实验班学生依赖图形计算器画图，师生都极少亲自描点作图，非实验班的同学没有机器可以依赖，尽管不能接触丰富的函数图象，可是所学的几个基本函数图象却是师生共同经历了计算、列表、描点、画图的过程，记忆相对深刻，考试中如果考查纸笔画图，他们未必处于劣势。看来，图形计算器在函数学习中的应用不能简单地仅画画图象，还应当将这一功能与纸笔运算、逻辑推理、列表作图之间达成一种平衡，更要发挥信息技术的优势，追求对数学知识的深刻理解。

学生在测验中的错误反映了他们并未真正明白对数函数在x = 0附近的变化情况，对这种“无限接近”的理解有困惑，于是，我提前引入“渐近线”的概念，首先列出函数值表,改变步长（分别设步长为Δx = 0.1, 0.001, 0.0001, ……），观察函数值在x = 0附近的变化，不论步长如何小，开头两行的函数值的差始终保持不变，体会第一行中“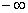”的含义；然后又回到函数图象，在应该有图象而没有显示出来的地方，用计算器的局部放大功能（zoombox）放大，屏幕上出现一段图象，它与y轴靠得很近，几乎与y轴平行。后来再次讨论函数时，我们也研究了它与函数的图象的关系，为了说明直线是函数的渐近线，仍然同时列出两个函数的函数值表，设步长为x=10，发现随着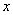的增大，两函数值非常接近，有一个同学突然发言“怎么当x=100时两函数值相等”，这与推理结论相矛盾的“意外”发现引起了学生们的兴趣，又有一同学提议输入函数看看，结果当x=100时函数值并不相等，经过讨论，终于认识到都是近似运算惹的祸，表格中的数据要求保留四位有效数字，两数的差如果小于0.01，屏幕上的显示结果一样，当时，与的前四位有效数字一致，但的第四位有效数字是小数点后第四位，因此，上述“意外”又在情理之中。用局部放大功能也显示，看起来重合的两条曲线事实上并没有重合，一次放大不清楚还可以二次放大，三次放大……，直到看清楚，就象显微镜一样，细微的关系也会明明白白呈现在你眼前。

这一案例让我体会到，学数学的真谛在于思考，同学们面对数学问题时，先不要急于按计算器，想一想，图象应该在哪几个区域，走势会如何，操作计算器验证，灵活应用多种功能，充分利用多元联系的表示方法，既要看得清楚，更要想个明白，所谓先想再操作；弄清了“是什么”，思考“为什么”，“怎么做”，“说明了什么”等才是深化对数学本质理解的关键。因此，我要求学生按照“想、作、思”的步骤使用计算器，动脑筋、勤思考才能学好函数。

案例2 函数图象大比拼

年轻人总是充满了好奇，学生应用计数算器绝对不仅仅限于教学内容，我们先来看下面来自学生心得体会的摘录：

同学A：“拿到计算器后，我不停地探索不同的功能，画许多函数的图象，通过不同符号的组合画不同的图象，记得曾画过心跳的图象，从1次到次，从指数到对数，一切想到的函数关系，都能找到一个图象，只有想不到，没有做不到，我们便开始比哪个的更怪异、更好看，寻求其中的对称美与不对称美。”

同学B：“学习函数时，有的同学课上课下都在玩计算器器，希望能够发现一块别人未曾找到的新大陆；同学们对于把这个计算器玩出名堂的人很崇拜。比如说刘效林，他在教大家如何表示绝对值时表情很神气，还有王海晨，他画出“耐克”函数之后，大家简直佩服得不了。

同学C：“还有一次我忽然想,,的图象是什么，于是就拿起图形计算器开始按，发现是一些奇怪的图形；如果没有计算器，这样的好奇心与想象力该如何满足？我可能永远不会去思考,,之类古怪的函数，计算器启发了我们的好奇心。”

同学D：“大家都满怀好奇进入这奇妙的数学世界，一回生二回熟，随着‘耐克函数’、‘麦当劳函数’相继诞生，我们画出的不仅仅是函数的图象，也是一些优美线条的组合，于是手中的计算器就活了，一到下课，前后左右的同学都拿出‘武器’来进行图形大比拼，比谁的图象最好看、最复杂、最新奇、最有美学价值，机器似乎变成了玩具，我们从中受益匪浅，脑中的数学世界活了，寓教于乐，两全其美，爱数学从图形计算器开始。”

同学E：一天，同桌拿着图形计算器给我看上面一个标准的阿迪达思标志，我想这不可能，因为它不可能是一个函数的图象呀，可眼前的一切都是真的，过后他悄悄告诉我，这是用描点画图搞出来的，我高呼上当，后来我也用这种办法将自己的名字弄到屏幕上，去骗那些还不知道这项技术的同学。又有一次当我输入时，发现它的图象是个半圆，我就想能不能弄出一个圆呢，和同桌研究了一节课，恍然大悟，再画一个和它对称的半圆不就行了，解析式应该是，输进去的结果正如所料，当时那份高兴难以形容。”

在许多学生眼中，数学是枯燥无味的，因此，让学生喜欢数学既是让学生学好数学的手段，也是改变数学在人们心目中形象的需要。引入图形计算器在一定程度上激发了学生学习数学的热情，但仅仅去追求一些新奇的、表面的东西就偏离了数学的本质。我在想，学生面对各种各样的图象时，想过为什么它会是这样吗？“耐克函数”、“麦当劳函数”这样的名字是怎么想出来的？同学怎么将与半圆联系起来的？通过个别交流、访谈，背后的故事给了我一些启发。

在整合本教材中我们讨论过函数，由于它的图象在第一象限的部分与耐克商标相象，一些熟悉的篮球迷对此倍感亲切，于是，在课堂上有同学将它命名为“耐克函数”，命名者受到大家的推崇，另一同学就想，其它著名商标有没有可以用函数图象表示的，因为他回家经常要路过一家麦当劳店，他想起了麦当劳标志，下课后他提出了这一想法，立即引起很多同学的兴趣。他们构造函数时首先想到图象应该关于轴对称、偶函数，但想到绝对值、二次函数、分段表示的是班上的数学高手。可见，真正的探究源于兴趣，创设情景很重要（这一次是同学自己创设的），很多人去研究，但往往只有少数人才能在关键处取得突破，而后通过交流，逐渐传播开来。过了一段时间，我进行了一次调查，提出问题者和率先解决问题者，以及少数几个主要传播者对情景还记忆犹新，能迅速写出解析式，多数同学知道有这么回事，但想不起解析式，也不知道如何解决这一问题。

两个案例都是发生在教学中的真实故事，既让我们看到图形计算器对教师教、学生学的有力支持，也让我们感到要让学生进行高水平的思维活动并非易事。按机器前先想一想，面对的数学问题是什么，猜想一下结果会怎样，估计一下走势或图象，操作中多动脑筋，切忌一按了之，对图象、数据的反思尤为重要，它既是验证一个问题的结束，更是另外一系列问题的开始，“想、作、思”应成为学习数学的一种习惯。

参考文献

刘艳云 应用图形计算器开发学生的创造潜能 数学教育学报，2004 年1期

黄荣金 技术支持下的数学教学探索 中学数学教与学 2003 年第2期

康杰 图形计算器在中学数学探究性学习活动中的应用 数学教育学报 2002年11期

史炳星 谈谈图形计算器对我国数学教育的影响 数学教育学报 2001年10期