信息技术为从不同角度看问题创造了条件

主题词 变量 身高 体重

数学是研究空间形式和数量关系的科学．而研究数量关系的一个主要方面又是研究两个变量的关系．我国现行高中教材，分别从函数、数列、回归分析三个角度对两个变量的关系进行了研究．但过去囿于传统的学习手段，相当数量的学生高中三年都难以从函数到数列到回归分析，循序渐进地对两个变量关系有一个系统的认识，特别是从确定关系发展到相关关系，不少学生更感到是一级难以跨越的台阶．自从学生利用信息技术学习之后，学习的内容和方式发生了变化，以往的状况得到了改变．这种改变主要体现在三个阶段的学习中：

一、函数学习为数列和回归分析的学习奠定基础

人民教育出版社《全日制普通高级中学教科书（必修）数学第一册（上）》（下称《必修》）“2.9函数的应用举例”和《普通高级中学实验教科书（信息技术整合本）数学第一册（上）》（下称《整合本》）“2.9函数的应用举例 建立实际问题的数学模型”中，都有这样一道例题：

以下是某地区不同身高的未成年男性的体重平均值表：

（1）根据表中提供的数据，能否从我们已经学过的函数y = ax+b，y = alnx+b，y=ab^x中选择一种函数，使它比较近似地反映出该地区未成年男性体重y关于身高x的函数关系？试求出这个函数解析式．

（2）若体重超过相同身高男性平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么该地区某中学一男生身高175cm，体重78kg ，他的体重是否正常？

这道题是2002年首先编入《整合本》，2003年才编入《必修》．对高一的学生来说，该题可以看作是一个函数拟合的问题，要解决这样的问题，离开信息技术可以说是寸步难行的．

解决这个问题的第一步，就是要根据已知数表作出散点图（图1）．当学生用图形计算器作出图1后，在认知上产生了冲突，函数图象怎么会是离散的点？可以用图象连续的函数来刻画离散的点吗？

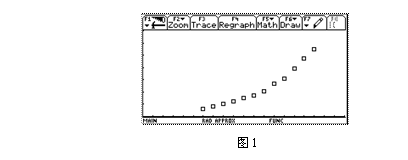
结合散点图，学生对实际中的变量间的关系有了新的认识，两个变量间的关系不一定满足严格的函数关系，其图象不仅可以是连续的直线或曲线，还可以是离散的点．这就为用函数的观点研究数列问题，以及对离散点进行回归分析奠定了基础．

解决这个问题的第二步，就是要根据散点图选择合适的函数模型．这是建立函数模型，刻画研究两个变量函数关系的关键．究竟应该在y = ax+b，y = alnx+b，y=ab^x中，选择哪种函数来反映体重与身高这两个变量的关系，这不同于以往那样，根据已知条件建立等量关系，而是要在学生原有认知的函数基础上进行选择，并要求学生对这些函数有深刻的理解．这种通过选择数学模型来刻画变量关系的思想方法，是建立函数模型、数列模型和回归模型的一种共同的思想方法．

解决这个问题的第三步，就是要根据已知数据求出函数解析式y=ab^x，即求a和b的值．一种方法是像《必修》一样，按学生已有的认知，选择两组数据，通过列方程来求．但应该选择哪两组数据？学生产生了困惑．其实，无论选择哪两组数据都只能近似地对实际变量进行描述．这就为今后认识回归方程奠定了基础．另一种方法是像《整合本》一样，直接将全部数据输入图形计算器，由机器直接得出结果，所得结果可能比《必修》的精确．但图形计算器是如何求出a和b值的？这给学生留下了悬念，同时又为建立回归方程埋下了伏笔．

最后，还要对所求模型进行检验．这是建立实际问题的数学模型不可缺少的一步．学生可以通过将已知数据代入所得函数解析式y=2′1.02^x，或作出所得函数的图象（图2），来检验所求函数能否较好地反映该地区未成年男性体重与身高的关系．

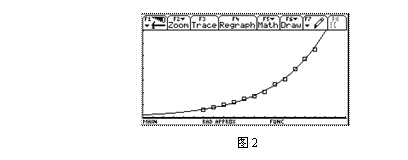
通过检验，学生会发现，尽管所得函数能较好地反映体重与身高这两个变量的关系，但毕竟还与实际存在误差．其实，对于许多实际问题，都难以建立数学模型，而对于那些可以建立数学模型的实际问题，又大多只能建立近似的数学模型，能被数学模型精确刻划的实际问题毕竟不多．这就为今后学习变量的不确定关系奠定了基础．

上述这种求函数模型的方法，与后面要学的回归分析的方法是一致的，其中用到的散点图又成了函数、数列、回归分析知识的一个交汇点，这就使得函数的学习为数列和回归分析的学习奠定了基础．

二、数列学习注重与函数的联系

由于有信息技术的支持，就为学生在数列的学习中保持与函数的联系创造了更为有利的条件．在引入数列的概念时，教师用的就是一个定义域为正整数集的函数实例，并从解析式、图象、表格三个方面进行诱导．并在数列的整个教学过程中，都强调与函数的联系．这就使得学生从一开始，就对数列是一种定义域为正整数集的函数有了认识，并能够像函数一样地对数列进行多元联系表示，用函数的思想方法来分析和思考数列的问题．

在课堂上，当老师再次把“2.9函数的应用举例 建立实际问题的数学模型”中的例子拿出来时，学生给出了下列三种表示（图3）：

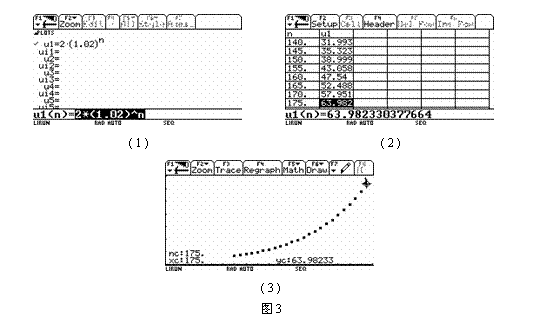
此时，学生对这一问题的认识，比学函数时更全面了．他们认为，如果将身高看作是取连续值的变量时，就应该从函数的角度来描述体重与身高的关系；如果将身高看作是取离散值的变量时，就既可以从函数的角度来描述体重与身高的关系，也可以从数列的角度来描述体重与身高的汇率换算关系．

通过信息技术的使用，在数列的学习过程中，学生丰富了函数的内容，加深了对数列的理解，进而在对两个变量关系的认识上有了新的发展，开始学会从不同的角度来研究客观世界中的变化规律．

三、在回归分析的学习中反思函数和数列的学习

有了上述函数和数列学习的基础，再对变量的关系进行回归分析时，学生对变量间的确定关系和不确定关系就容易形成辩证的认识．在回归分析的教学中，教师又一次与学生一起对“2.9函数的应用举例 建立实际问题的数学模型”中的例子进行研究．选择y=c?edx来反映体重与身高的关系，令z＝ln y，a＝ln c，b＝d，通过线性回归，可得到线性方程z＝0.019711x＋0.695 157，进而得到了新的解析式y=2.004 024e ^{0.019 711x}及其曲线（图4）．学生从中学会了如何求与离散点最接近的图象，放下了最初建立函数模型时留下的悬念，明白了当时图形计算器是如何求出解析式y=ab^x中a和b的值（a＝2.004 024 ?2，b＝e ^{0.019 711} ?1.02）．

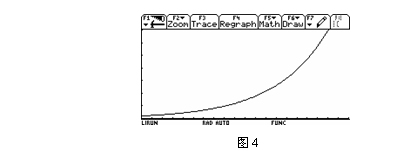
在对问题进行了回归分析之后，教师让学生把三次研究的过程和结果作了对比，经过回顾与反思，学生建立了函数、数列与回归分析三者之间的联系，对体重与身高两个变量间的关系有了更深刻的认识．

同一个问题研究了三次，历时两年多的时间，利用信息技术为学生分别从函数、数列、回归分析三个不同的角度，多元联系地看问题创造了条件，让学生对两个变量关系的认识有了循序渐进的发展．