一道概率习题的教学

主题词 计算器 二项分布 概率

人民教育出版社《普通高级中学实验教科书（信息技术整合本）数学第三册》“习题1.1”新增了这样一道题：

一份某种意外伤害保险费为20元，保险金额为45万元．如果某城市的一家保险公司一年能销售这种保单10万份，所需成本为5万元，而需要赔付的概率为10－6．那么用图形计算器或计算机求：

（1）这家保险公司亏本的概率；

（2）这家保险公司一年内获利不少于100万元的概率．

在二项分布的课堂教学之后，教师将这道题作为课外作业布置给了学生．学生们对这一问题产生了浓厚的兴趣，他们认为，这是一个与现实很贴近的问题，例如航空意外伤害保险就是如此．但没有想到的是，绝大多数学生第1小题都没能得到正确答案．原因出在哪里？下面是一份具有代表性的作业：

解：（1）设1年内需要赔付的人数为X，则X~（10⁵，10^－6），所以这家保险公司在这1年内要赔付450 000X元．

因为保险公司1年的销售收入为

10⁵í20＝2í10⁶（元），

所以要使这家保险公司亏本，则必须

450 000X >2í10⁶，

即

X >．

因此，这家保险公司亏本的概率为

P(X >4)＝＝？

原来学生的问题是出在不能求出的结果．一些学生认为，这一式子的运算量太大，别说用笔无法运算，就是用计算器也无法运算．所以在作业点评时，教师就以“如何计算”为题，让学生展开讨论．经过讨论，学生们提出了下面几种解法：

解法一：

＝1－，

将上式输入图形计算器

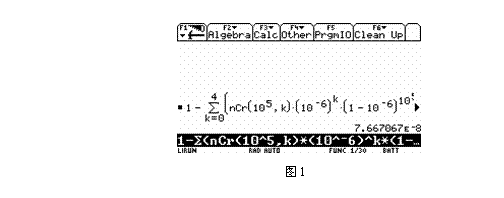
可得

　　　　　　原式＝7.667 067í10^－8．

解法二：

＝1－

＝1－―

― ―

―，

用科学计算器可得

　　　　原式＝1―0.904 837 373―0.090 483 828―0.004 524 151

―0.000 150 802―0.000 003 77

＝7.6í10^－8．

解法三：作出运算的程序框图

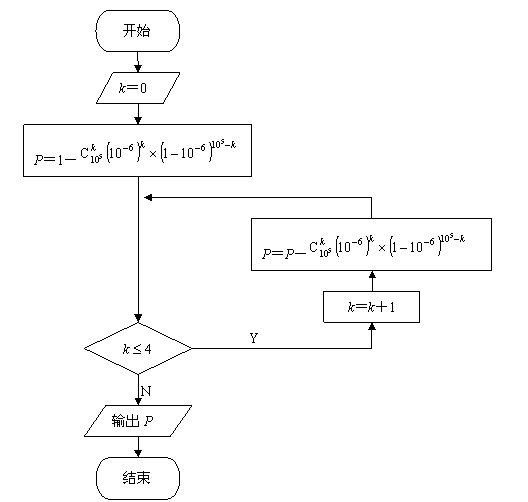
根据框图编写程序（略），然后在计算机上运行，可得到更为精确的解．

在得到以上解法之后，有学生又提出，如果没有信息技术工具的帮助，像原题这样的问题怎么解决？

带着学生的疑问，教师对知识进行了拓广，从而继续将问题引向深入．此时，教学没有受教材内容的局限，适时地向学生介绍了泊松分布．由于本题中的n很大，p很小，因此可以用l＝np＝0.1的泊松分布近似替代二项分布，于是

P(X >4)≈1－＝7.667 801í10^－8．

通过这道题的教学，使我们看到：

一、信息技术使教材的内容发生了变化，为学生的学习提供了更加丰富的情景．如果没有信息技术的支持，像这样的问题，学生就不能用所学的二项分布知识来解决，一般也只能用泊松分布近似地替代二项分布来解决．这样，就限制了教材的内容，使学生的学习存在很大的局限性．

二、学生的上述解法都有一个共同点，那就是都利用了离散型随机变量分布列的性质，将变形为1－．许多学生正是由于没有作这样的变形，即使用了信息技术工具也难以得到最后的结果．这说明，使用信息技术工具并没有降低对学生计算能力的要求，它使学生避免了简单繁琐的运算，而在算法这一更高层次上向学生提出了新的要求．

三、上述三种不同的解法体现了使用信息技术工具解决问题的不同层次要求．解法一最简便，但只能用具有代数运算系统的计算机或图形计算器才能完成；解法二最繁琐，但只要具有组和数运算功能的科学计算器、图形计算器和计算机都能完成；解法三最能体现学生的算法思想，但只能用计算机才能完成．这说明，在学习中要注意使用信息技术的广泛性，应根据不同的学习任务，选择适当的信息技术工具，从而有效地进行数学学习．

像这样，学生在解决问题的过程中遇到困难，根据需要自觉地去选择信息技术工具，探求结果，从而引发对问题解决的广泛思考，这不能不说是信息技术给学习方式带来的变化．