三次函数性质的探索

主题词 探索 三次函数的性质 极值

我们已经学习了一次函数，知道图象是单调递增或单调递减，在整个定义域上不存在最大值与最小值，在某一区间取得最大值与最小值．那么，是什么决定函数的单调性呢？利用已学过的知识得出：当k>0时函数单调递增；当k<0时函数单调递增；b决定函数与y轴相交的位置．并结合TI图形计算器任意输入几个不同的一次函数进行验证．

接着，我们同样学习了二次函数，图象大致如下：

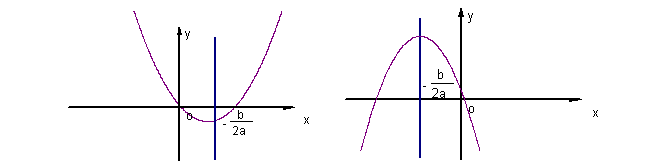
　　 图1                            图2

利用已学知识归纳得出：当时(如图1)，在对称轴的左侧单调递减、右侧单调递增，对称轴上取得最小值；当时(图2)，在对称轴的左侧单调递增、右侧单调递减，对称轴上取得最大值．在某一区间取得最大值与最小值．其中a决定函数的开口方向，a、b同时决定对称轴，c决定函数与y轴相交的位置．应用用TI图形计算器任意输入几个不同的二次函数进行验证．

那么，三次函数的图象是什么形状呢？单调性呢？是否存在极值？它有哪些性质呢？各组学生开始对函数图象可能单调递增、有极值等问题展开激烈讨论．接着让各小组利用TI图形计算器任意输入几个不同函数进行验证．学生马上输入许多不同的三次函数进行探索，经过各组学生探索后，综合他们的探索归纳发现函数有六类．如图：

图3 　　                      　　 图4

图5                                 图6

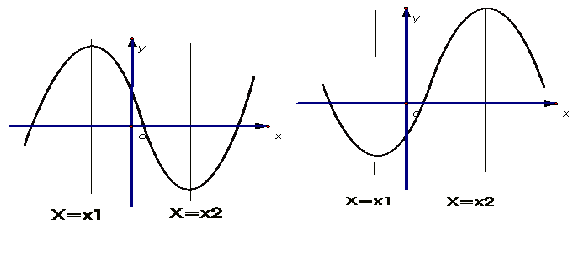
图7                               图8

分析：由图3函数有哪些特点呢？归纳：解析式是，整个定义域上函数单调递增，在图4中解析式是，整个定义域上函数单调递增减．整个定义域上不存在极值，函数必经过原点．单调性又与什么知识相关呢？导数，现在求出函数的导数是，验证与0的关系，当时，即的图象在是单调递增；当时，即的图象在是单调递减相一致．当，根据图象知道，在处不是函数f(x)的极值点．所以的根是函数取得极值的必要不充分条件．现在思考并验证函数与函数图象有什么关系？经过验证得出：函数与相同，当时函数图象是图象向上平移|d|个单位；当时函数图象是图象向下平移|d|个单位；函数的导数都是．

在图5中解析式是，整个定义域上函数单调递增．在图6中解析式是，整个定义域上函数单调递增减．整个定义域上不存在极值．函数的导数，经过验证在图5中因为即，所以的图象在是单调递增；在图6中因为即，所以的图象在是单调递减；函数都不存在极大值或极小值．为什么在图5中a>0、,在图6中a<0、呢？a>0、或a<0、是又有什么结果呢？因为导数是二次函数，当a>0、或a<0、时判别式，导数函数不小于0，方程有一个根．当a>0、或a<0、时，方程有两个根．那么函数图象有什么特点呢？猜想如果，那么有两根，函数f(x)应有增也有减，我们来验证一下图7、图8：

在图7中解析式是，在或上函数单调递增，在上函数单调递减；在处取得极大值，在处取得极小值；在图8中解析式是，在或上函数单调递减，在上函数单调递增；在处取得极小值，在处取得极大值，它们在上最大值和最小值．为什么呢？函数的导数是，设的两根是并且令．经过验证在图7中，因为，当或时，所以的图象在或是单调递增；在上，所以的图象在是单调递减．在图8中，因为，当或时，所以的图象在或是单调递减；在上，所以的图象在是单调递增．

经过上述探索知道，函数在整个定义域上是单调递增（递减），左右都增中间递减，还是左右都减中间递增，是由a确定，b、c确定函数有没有极值、d确定函数与 y轴的交点．并且函数单调递增（递减）有没有极值与的导函数的判别式相关，具体归纳如下性质：

设的导数是则，函数的判别式为：由导数的图象可知：

时导数的图象 　　　　　　　　　　　　时导数图象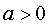
　　　　　　　　　　　　　　　　　　

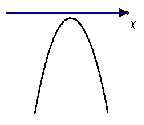
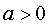
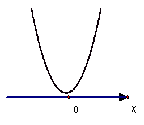
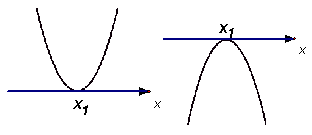
图9 　　　　　　　　　　　　　　　　　　　图10

函数f(x)图象　　　　　　　　　

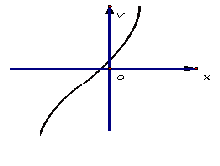
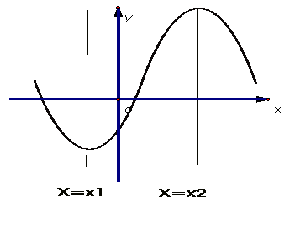
图11　　　　　　　　　　　　　　　　 图12

三次函数f (x)在R上是单调函数，（无极值）
　　时的两根为且导数图象
　　　　　　　　　　　　　　　　　　　　　　　　　

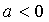
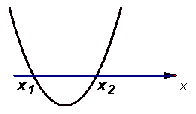
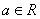
图13

函数f (x)图象 　　　　　　　　　函数f (x)图象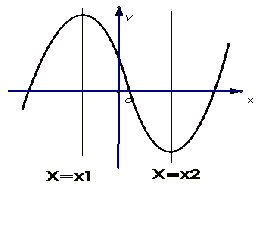
　　

图14　　　　　　　　　　　　　　　　　　 图15

1、时在或单调递增；在单调递减(如图14)在处取得极大值，在处取得极小值．

2、时在或单调递减；在单调递增，(如图15)在处取得极小值，在处取得极大值．

注意：三次函数f(x)有极值导函数的判别式>0

根据以上性质可以灵活解决三次函数问题：

例1、设，讨论关于x的方程的相异实根的个数？

解：分析：要讨论方程根的个数，直接求解非常困难，根据题意，需把方程转化为函数问题，即方程变成，设，这转化为讨论函数与交点的个数．

函数的导数的两根为(如图16)

  函数的极大值是，函数的极小值是，

（1）当或时，函数与只有一个交点，即方程只有一个根．

（2）当或时，函数与只有两个交点，即方程只有两个根．

（3）当时，函数与有三个交点，方程有三个根．

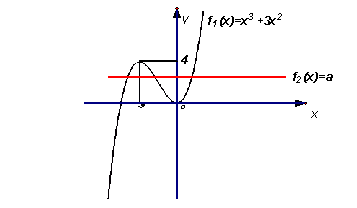
图16

例2、已知函数是R上的奇函数，当时f(x)取得极值．

（1）求f(x)的单调区间和极大值；

（2）证明对任意，，不等式恒成立．

解：（1）函数f(x)是奇函数，所以，函数f(x)的导数依题意得,,解得

所以导数，(如图17)
　　时，函数f(x)单调递增；

时，函数f(x)单调递减；所以．

（2）如图17 对任意，， 函数f(x)单调递减，所以

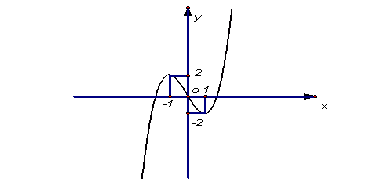
图17

一般地在导数有两根且时，在处；在处，对任意都有

因此，我们利用信息技术能够轻松研究三次（高次）函数的性质，同时验证了高次函数与导数知识的关系，使学生既学到了新知识，又巩固了旧知识，充分利用好信息技术的直观显示，能更有效解决三次函数的极值、某一区间的单调性、证明不等式等问题找到较好的解决办法．