提要 通过学生完成一个课堂练习的案例,发现广泛使用信息技术能激发学生积极的思维活动,学生在选择信息技术的过程中,便从不同角度加强了对数学概念的理解,使得信息技术的使用与数学学习相辅相成,协调发展.
主题词 信息技术 随机数 白球
人民教育出版社《普通高级中学实验教科书(信息技术整合本)数学第三册》“1.1离散型随机变量的分布列”的“练习”有这样一道题:
先用计算器或计算机模拟下列随机试验,然后与其他同学交流,看大家在计算器或计算机中设置的随机变量的取值是否相同?
一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球的个数.
学生对随机变量取值的看法基本上都一致,设所取的3个球中白球的个数为X,则随机变量X可取0,1,2,3.X=i表示取出i个白球,3-i个黑球,其中i=0,1,2,3.但对模拟随机试验,大家就有不同的看法.下面给出几种学生的解法:
解法一、利用科学计算器进行模拟,用1,2,3,4,5分别表示5个黑球,6,7,8,9,10分别表示5个白球.操作步骤如下:
|
序号 |
按 键 |
显示内容 |
备 注 |
|
1 |
PRB ,?,?,?,?, |
RANDI( |
选择随机整数菜单 |
|
2 |
1 ,2nd, ) ,10, ) |
RANDI(1,10) |
输入随机整数的范围 |
|
3 |
|
RANDI(1,10) 6 |
每回车一次便可产生一个1~10的随机整数,连续回车3次,即表示进行了一次试验 |
解法二、利用TI-92图形计算器进行模拟,用1,2,3,4,5分别表示5个黑球,6,7,8,9,10分别表示5个白球.操作步骤如下:
|
序号 |
|
画 面 |
备 注 |
|
1 |
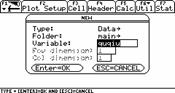
APPS ,6 ,3 ;对Type选Data,拨动光盘,对Folder选main,在Variable中输入文件名,ENTER |
|
创建统计数据表格 |
|
2 |
ENTER,拨动光盘,将光标移到c1上,ENTER,在命令行上输入c1=rand(10) ,ENTER;同理,输入c2=rand(10) ,c3= rand(10) ,c4=when(c1=c2 or c1 =c3 or c2=c3,undef,ceiling((c1-5)/5)),c5=when(c1=c2 or c1= c3 or c2=c3,undef,ceiling((c2-5)/5)),c6=when(c1=c2 or c1= c3 or c2=c3,undef,ceiling((c3-5)/5)),c7=c4+c5+c6 |
|
打开统计数据表格,在c1列、c2列和c3列分别输入1~10的随机整数;c1、c2、c3互不相等时,分别在c4、c5、c6列输入 |
|
3 |
拨动光盘,将光标移到c7上,ENTER,ENTER |
|
每当光标移到c7上并回车后,都将得到一组新的数据,表示所取的3个球中白球的个数 |
解法三、利用计算机中的Excel进行模拟,用1,2,3,4,5分别表示5个黑球,6,7,8,9,10分别表示5个白球.操作步骤如下:
|
序号 |
步 骤 |
画 面 |
备 注 |
|
1 |
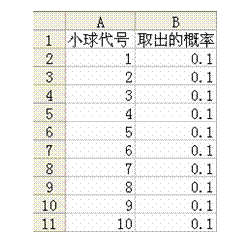
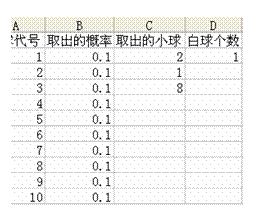
打开工作簿,分别输入小球代码和各小球被抽取的概率. |
|
创建小球代码工作簿 |
|
2 |
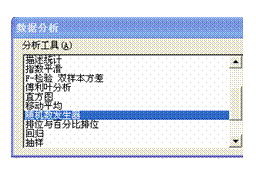
在“工具”菜单中选择“数据分析”选项,弹出“数据分析”对话框 |
|
|
|
3 |
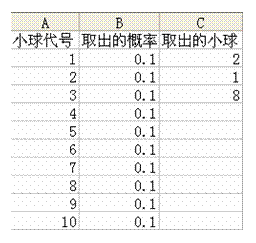
在“数据分析”列表中双击“随机数发生器”选项,打开“随机数发生器”对话框.分别输入变量个数和随机数个数;选择离散分布;在数值与概率输入区域中输入A2~B11单元格;选择输出区域,输入C2 |
|
利用随机发生器从1~10这10个数中,随机地产生3个数 |
|
4 |
单击随机发生器中的“确定”按钮 |
|
每次产生3个随机数 |
|
5 |
在单元格D2中输入“COUNTIF(!$C$2:$C$4,“>=6”)” |
|
统计单元格C2~C4中,所有大于或等于6的单元格的数目,即取出的白球个数 |
对上述解法,学生发表了自己的观点:
一、解法一较为简单,采用此方法的人数也最多.采用此方法的学生提出,题目要求从袋中取出3个球,但没有说怎样取.所以他们以为,可以理解为分3次取,每次有放回地取出1个.
二、持解法二的学生认为,可将题目理解为分3次取,每次不放回地取出1个.由于在图形计算器上不易模拟这一试验,所以他们采取先模拟可放回地取出,再将重复取出同一个球的试验去掉,只考虑取出不同球的情况.这一方法直观地反映了每次试验取出的白球个数,即随机变量的取值,利于对取出不同个数白球的概率的研究.
三、持解法三的学生较少,但他们认为,自己设计的解法是所有解法中最优的.这一解法是建立在将题目理解为一次取出3个的基础上.与解法二一样,它不仅直观地反映了每次试验取出哪3个球,还反映了取出的白球个数.
学生们各持己见,讨论很激烈.在此基础上,教师提出了以下问题:
1.如果本题是分3次取,每次有放回地取出1个,那么在所取出的3个球中,含白球的个数分别为0,1,2,3的概率分别是多少?
2.如果本题是分3次取,每次不放回地取出1个,那么在所取出的3个球中,含白球的个数分别为0,1,2,3的概率分别是多少?
3.如果本题是一次取出3个,那么在所取出的3个球中,含白球的个数分别为0,1,2,3的概率分别是多少?
通过解决以上问题,学生认识到,每次不放回地取出1个,与一次取出3个的结果相同;而每次有放回地取出1个,与另两种取法的结果不同.所以,解法二和解法三的本质相同,而解法一则属于独立重复试验,与另外两种解法完全不同.
在这道练习题的教学中,学生所使用的信息技术是广泛的,正是由于信息技术的广泛运用引发了学生的思考.学生通过对不同信息技术的分析,不仅提高了运用信息技术解决数学问题的水平,还加强了对离散型随机变量、独立重复试验等概念的理解,同时为离散型随机变量的分布列的教学奠定了基础.这正是信息技术对改变教和学的方式,促进学生认知的一个集中体现.