数学能力是一种特殊的能力，是顺利完成数学活动所必须具备的稳固的心理特征。这种能力是在数学活动中形成和发展的，并表现出一种数学学习的能力。培养学生的数学能力是中学数学教学的主要目的之一。要培养学生的数学能力，必须通过解题从解题中学会西考问题，解决问题并且探索出规律。因而习题的选择，对我们数学教师来说就是显得非常重要。根据教学内容选取必要的，恰当的习题，就能顺利地完成教学目标，培养学生地数学能力。
一． 讲授新概念理解新知识，选取针对性的习题
在数学教学过程中，当讲完新概念，公式，定理或法则之后，针对教材重点而学生又容易忽视，出错的地方，设计一些习题。如讲完向量有关概念之后，为了加深学生的理解，设计如下两题：
1． 判断下列命题的真假：
（1） 若
，则
（2）若
＝0，则
＝0
（3） 两个向量相加的充要条件是：他们的起点和终点分别相同。
（4） 在平行四边形
中，
2．下列命题正确的是（ ）
,则
；
若
,则
一定组成平行四边形；
若
，则
；
若
，
，则
。
二． 为了挖掘有关知识的本质，要选择一组具有规律性的习题
这类习题能够培养学生思维的深刻性，体现出学生的概括，归纳能力，抓住知识的本质和规律。如三角证明题：
（1） 若
,则
。
（2） 在
中，求证：。
（3） 若
，则：。
根据以上习题的练习，可得出以下规律：如果三个角满足
（
），都有
，其证明方法是根据两角和的正切公式及诱导公式。由此学生就能根据规律很自然很顺利地证明问题。
三． 为了解决教材地重点，突破难点，应选择一些典型性比较强地习题
这类典型的习题，具有较强的代表性。对这类习题的讲解和练习，可以清晰地反映出知识地实质，使学生对知识重点地理解，难点地突破起着关键性的作用。如在求三角函数有关最值问题时，给学生配备了如下地习题：
（1） 求函数
的最值
简解：
，所以
，
。
（2） 求函数
的最值。
简解：令
所以，
当
时，
；当
，
（3）函数
，在
取得最大值，在
时取得最小值，则
必须满足（ ）
0≤≤
≤≤ ≤ ≥
通过以上典型习题的练习，使得学生对有关三角函数求最值这部分知识有了更深的理解，其求法基本上是由三角函数的有界性和二次函数在闭区间上的最值求法求解。
四． 拓宽学生视野，培养学生多向思维，应选择一题多解的习题
数学中的许多习题，都有多种解法，我们做教师的在教学过程中，应根据教材特点和学生实际选择一些一题多解的习题。
如：已知数列
，
，求
。
解法（一）（递归法）：
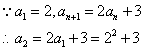
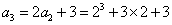
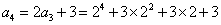
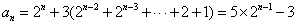
解法（二）（累积法）：
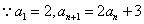
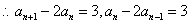
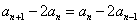
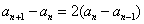
累积得
，与
联立得
，
当
，显然也满足此式，故
解法（三）（换元法）
由法（二） 
，故
是以2为公比以
为首项得等比数列
以下同解法（二）
解法（四）（待定系数法）
由
得，
，得
即可变为
，以下同解法（二）
解法（五）（数学归纳法） 略
通过以上多角度多方位寻求问题得解决途径，活化了学生得数学知识和数学技能，使学生的思维变得灵活主动，培养了学生思维的广阔性，深刻性和创造性。
五． 培养学生的解题的灵活性，应选择有技巧性的习题
解题技巧指解题方法的技巧。这种技巧来源于对基础知识的准确把握，来源于学生的 解题经验等。加强技巧性习题训练对培养学生的数学解题能力銅價有很大帮助。
如：（1）解方程
解：有方程可知：
成等差数列，
故可设
，
两式平方相加得
，代入假设可求得
或3
经检验都是原方程的解。
（2）（93年高考题）在各项均为正数的等比数列中，若
，则
（ ）
简解：因为
，所以原式的结果是10。或者本题可以设，也可以很快得到结果。
（3）（2000年高考）过抛物线的焦点F作一直线交抛物线于P,Q两点，若线段PF与PQ的长度分别为
，则
（ ）
简解：可选取过焦点
垂直于
轴的直线，则
，所以
六． 培养学生用综合知识分析问题和解决问题的能力，要选用综合性习题
这类习题可强化学生对各部分知识的衔接和知识系统化的把握，能够培养学生思维的独创性和全面性，是培养学生分析问题，解决问题的能力的重要途径。有关例题省略。
长期通过以上各类习题的训练，不仅使学生对所学的各个层面上的知识的理解和把握有很大帮助，而且使学生的数学思维能力，运算能力，空间想象能力及解决数学问题的灵活性的能力有较大提高。选择在有限时间内通过有限的习题的训练，达到了提高学生数学能力的目的，也就大大提高了学习效率。