提要 随着计算机技术的高速发展和在各个领域中的广泛应用,我国中学数学教学中也越来越普遍的使用了计算机进行教学,在把普通计算机应用于数学教学的同时,另一种信息技术教学的工具──“图形计算器”也在逐步得以推广.本文是在新课改的指导下.以“信息整合教材”为基础,调查、了解了曲靖市民族中学高一《数学》信息整合教材实验班使用情况的前提下,主要介绍了信息技术的重要性,TI图形计算器的功用在中学数学教学中的作用,并以实际课例来说明TI图形计算器在具体教学中的实施及实施效果,对提高信息时代的数学教育意识有一定的积极作用.
主题词 TI图形计算器 信息技术
有人说21世纪的教育应当是信息技术的应用教育,1999年教育部的《面向21世纪教育振兴行动计划》中也提到了信息技术教育.特别是在一大批新的应用数学学科(例如信息论、控制论、运筹学、数理经济、金融教学……)中结合计算机的应用形成了数学技术.实际上数学技术这个术语的出现本身就标志着数学的应用达到一个新的阶段,也是为适应社会发展需要,转变数学教育观念的一种飞跃.
由于计算机和信息技术的迅速发展以及对教育产生的日益增大的影响,有的专家指出:“我们正处在孩子们的学习和思考方法根本变革的早期阶段”“知识将日益通过经验而不是被动地消化事实来获得”.所有这些都把教育特别是数学教育(以及和科学,技术教育的结合)放在特别重要的地位,强调了信息技术对教育的重要性,它从根本上改变了数学世界.
而随着计算机技术的高速发展和在各个领域中的广泛应用,我国中学数学教学中也越来越普遍的使用了计算机进行教学,在把普通计算机应用于数学教学的同时,另一种进行教学法的工具──“图形计算器”也在逐步得以推广.实际上,图形计算器可以看成一个具有专用功能的小型计算机,它具有学生学习数学最需要的计算和作图的各种功能.和普通计算机相比,它便于携带,使用方便,功能专一,既可以供教师在备课过程中或课堂教学演示时使用,也是学生学习和应用知识时的现代化学习工具.它的投入使用无形给数学教学带来了方便,大大节约了繁杂的计算作图所浪费的时间.从曲靖市民族中学实验班(现已高二)实验结果调查来看,效果是非常明显的.在此为倡导信息技术教育,转变教学观念,总结经验,加强交流,附使用图形计算器课例一个以促进图形计算器进行中学教学工作的开展.
正弦函数和余弦数函数的图象
[教学目的] 使学生理解并掌握利用单位圆中的正弦线和余弦线作出正弦函数和余弦函数的图象.
[教学方法] 使用TI──92Plus图形计算器中的“几何画板”进行教学.
[课时安排] 1课时
[教学过程]
一、引入
提问:如何作出正弦函数y=sinx和余弦函数y=cosx的图象?(x∈[0,2π])的图象,回答:描点法.并互相交流,然后用图形计算器绘出图象检验自己的画图结果.使学生明确,描点个数越多,画出的图象越精确.但由于我们在描点时取得是近似值,因此误差较大,影响了作图的准确性.
我们知道,利用单位圆中的三角函张线,能将比较抽象的三角函数值表示成形象的有向线段,从而可把三角函数的某些问题转化为几何问题得到解决.
二、新课讲解
1、复习单位圆中的三角函数线.
如图1,单位圆中的有向线段MP表示角x的正弦值,有向线段OM表示角x的余弦值,即MP=sinx,OM=cosx.
[说明]按钮“P”可使点P在圆上运动,演示角x在四个角限中的三角函数线;按钮“MP”和“OM”可使有向线段MP和有向线段OM闪动.
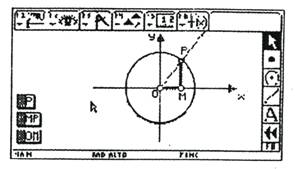
图1
2、函数y=sinx(x∈[0,2π])图象的几何作法.
(1) 按钮“py”可将单位圆中角x的正弦线MP沿x轴平移到直角坐标系内的M′P′处,且使得OM′=x,那么点P′的坐标为(x,sinx)如图2.
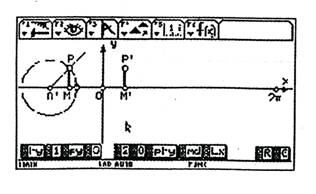
图2
(2)使用按钮“md”在直角坐标系内描出一系列点P′(x,sinx)如图3.

图3
(3)按钮“Lx”用光滑曲线把这些正弦线的终点连接起来,就得到了正弦函数y=sinx x(x∈[0,2π])的图象如图4.
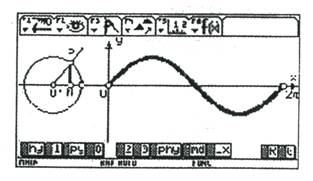
图4
3、因为终边相同角的三角函数值相等,所以正弦函数在…,x∈[-2π,0]),x(x∈[2π,4π],…时的图象与x∈[0,2π]的图象形状完全一样,只是位置不同.我们只要把正弦函数y=sinx (x∈[0,2π])图象向左和向右平行移动2π个单位长度4π单位长度,……,就可以得到y=sinx(x∈R)的图象如图5.
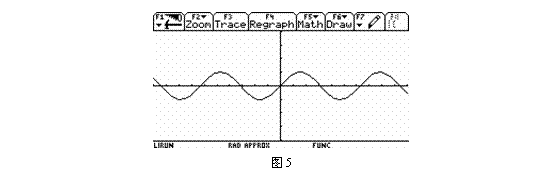
4、学生练习正弦函数y=sinx (x∈[0,2π])的图象的几何作法.
5、余弦函数y=cosx (x∈[0,2π])的图象的几何作法.
(1)为了避免图象的重叠,不妨将坐标系向下平移,并把单位圆中角x的余弦线OM平移到O′N处(按钮“py”).为使“横”在x轴上的余弦线O′N“竖立”起来,我们过点O′作与x轴的正半轴成角为45o的直线,再过N作x轴的垂线,与此直线交于点Q,那么有向线段OM、O′N和NQ的长度相等且方向相同,我们就把余弦线O′N“竖立”起来成为NQ(按钮“11”)如图6.
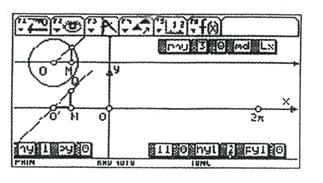
图6
(2)按钮“pyl”可将N′Q′沿x轴平移到坐标系内的NO处,使得ON′=x,那么点Q′的坐标为(x,cosx)如图7.
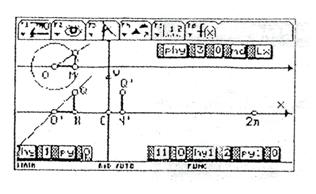
图7
(3)使用按钮“md”在坐标系内描出一系列点Q′(x,cosx)如图8.
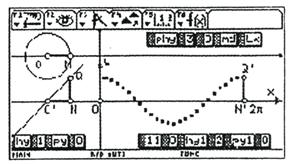
图8
(4)按钮“Lx”用光滑曲线把余弦线的终点连结起来,就得到了余弦函数y=cosx (x∈[0,2π])的图象如图9.
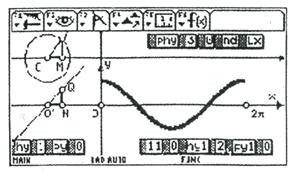
图9
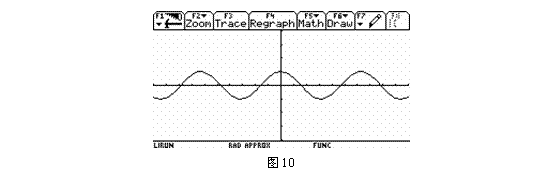
(5)把余弦函数y=cosx (x∈[0,2π])的图象向左和向右平行移动2 π个单位长度,4 π个单位长度,…就可得到y=cosx(x∈R)的图象如图10.
6、学生练习余弦函数y=cosx (x∈[0,2π])的图象的几何作法.
7、让学生观察正弦曲线和余弦曲线的形状和位置的特点,比较它们的异同.
三、小结
1、正弦函数和余弦函数图象的几何作法的主要步骤.
2、利用几何作法,可以得到比较精确的作法,利于通过图象的直观总结函数的性质.
四、作业 高中代数上册第169页练习.
总结:通过这一堂教材与信息技术的整合教学,既保留了传统教学的重心,又发挥了信息技术的优点──直观性,容量性,方便与节时性.因此建议把教材与信息技术的整合教学进一步的深入下去.