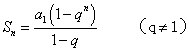数学思想的教学途径

一、深入分析教材，挖掘教材内在的思想和方法

数学思想方法是前人探索数学真理过程的积累，但数学教材并不是这种探索过程的真实记录，恰恰相反，教材对完美演绎形式形式追求往往掩盖了内在思想方法，颠倒了数学真理发现过程，所以一方面要不断改革教材，使数学思想方法在教材中得到较好反映与体现；另一方面要深入分析教材，挖掘教材内在的思想和方法。

突出数学思想方法是改革教材的一个重要方面。如，江苏省编写的实验教材，从本身的实际状况和发展需要出发，在教材里安排了较多的选读内容，学生通过奇偶分析、群、序、特殊与一般、估计、交集、分离系数法、限制与扩张、分析分式、观察法等读一读“材料”的学习，不仅可以扩大知识面，而且可以受到更多的数学思想方法的熏陶和训练。

其次，教师要深入地分析教材，以挖掘和领会教材内在的思想和方法。对教材进行逻辑分析，除了把握教材的体系与脉络、地位与作用、重点与难点之外，还要按照知识──方法──思想的顺序，从知识中挖掘方法，从方法中提炼思想，使教材分析具有较高的观点。如，在三角恒等变形中，有很多公式、变形方法和技巧，题目更是大量。教师要能从中揭示出“分析差异、实施变形、消除差异”的基本思想，把握三角变换的精神所在。又如，对立体几何教材进行分析，不仅要把握它的内容、地位、作用等，而且应从数学思想方法的角度认识它的显著特点：①将一些空间图形问题转化成平面图形的问题去解决；②利用空间图形与平面图形相似关系，类比地由平面图形的性质去探求空间图形的有关性质，寻找更好地解题途径。教学中，如果抓住这两点，犹如交给学生学习立体几何的钥匙，它们正是立体几何的精神和灵魂。

欲使数学思想方法的教学落实到实处，备课时不仅要明确章节和课时教学的知识点，还要列出知识与思想方法结合的交叉点。例如：对“数列”一节内容知识点、蕴含的思想方法及结合点可作下表分析：

二、重视教学过程，加强思想方法的训练和培养

数学教学过程，大体可分为知识发生和应用两个阶段。前者指揭示和建立新旧知识的内在联系，使学生得到新知识的过程；后者指对己有的概念、定理、公式、法则和方法的巩固和应用中进一步理解的过程。

《新课标》指出，在进行概念教学时，应当让学生了解概念、结论等产生的背景、应用，理解基本的数学概念、数学结论的本质，体会其中所蕴涵的数学思想和方法，以及它们在后续学习中的作用，通过不同形式的自主学习、探究活动，体验数学发现和创造的历程。因而教师在此过程中，需要向学生提供丰富的、典型的、正确的发现背景材料让学生在老师指导下，对感性材料进行分析、综合、比较、分类、抽象、概括、系统化、具体化，这不仅是对数学思维方法的极好训练，也是对数学抽象与数学模型方法觉悟的极好机会。如讲授排列概念时可通过下面的感性材料：

（1）北京──上海──广州三个民航公司的直达航线，需要准备多少种不同的机票？

（2）由数字1、2、3可以组成多少个没有重复数字的两位数？

让学生通过一系列的思维操作，从中抽象共同特点，即均可看成从三个不同元素中，每次任取两个元素，按照一定的顺序排成一列，问有多少种不同的排法──抽象成相同的数学模型，进而得出排列定义。这样得到的就不只是排列概念，还受到了数学思想方法训练与熏陶。

需要指出，有些数学的概念本身就蕴含着某种思想方法，例如，数的绝对值和算术根的概念中蕴含着分类思想；复数相等概念中蕴含着转化思想。又如，几何中诸角和距离概念中也蕴含着转化的思想。立体几何中，面与面、线与面、两异向直线的成角都是转化为平面几何中线与线的成角来给出定义的。同样互相平行的面与面、线与面的距离均在转化为点到平面的距离，点与面、点与线、两异面直线的距离最终又转化为点与点之间的距离来给出定义。

对于规律（定理、公式、法则等），也要重视其发生过程的教学，教师也应当善于引导学生通过感性的直观背景材料或己有的知识发现规律，不过早地给结论，弄清抽象、概括或证明的过程，充分地向学生展现自己是怎样思考的，使学生了解蕴含其中的思想方法。如，立体几何中直线与平面垂直的判定定理，其证时过程要分数种情况，添9根辅助线如照本宣科地将定理证明一遍，似乎完成了教学过程，然而所展现的仅是演绎推理过程，它掩盖了证明思路的分析过程。应该明确，分析的重点是添辅助线的探索和思考过程。事实上，该定理还可采用不同的构造方法，如学生自制筝形模型，按照观察──猜想──证明──总结步骤，从平面到空间，从具体到抽象，从特殊到一般，让学生自己去发现和证明。这些探索活动，能使学生得到更多数学思想方法培养和训练。

同样还需指出，许多数学定理、公式、法则的证明过程。就蕴含着某种思想和方法，如等比数列前n项和的公式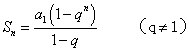, 推导过程蕴含着分类、转化思想和错位相减法的求和方法。

总之，在教学的每一个环节上，都要有意识地引导，抓住传播数学思想方法的每一个机会，长此训练和培养，学生才能逐渐步入数学思想方法的自由王国。

三、搞好整理总结，进行思想方法的概括和提炼

数学思想方法隶属性的特点，决定了它的教学形式主要以数学知识为载体，并按分散的形式进行，这种教学形式不仅符合数学思想方法自身特点，也符合学生的认知规律，学生在潜移默化的影响下逐步感受、领悟和掌握数学思想方法。

比如,在集合单元复习时，可以在平时渗透性教学的基础上进行小结，提炼出交集法、并集法、训集法等方法，进而概括出“把所有考察对象征作为一个整体（集合），然后利用集合概念表示运算来解决问题的思想──集合思想”。还可以通过范例，从横向对其符合表示思想、分类讨论思想、数形结合思想、转化变换思想进行概括，以促进学生数学思想的形成和发展。

再如，通过对立体几何内容的复习，可对其转化的思想方法进行了整理和小结：①把“高维”转化为“低维”（常通过截、展、平移、旋转以降维）；②把“一般形体”转化“特殊形体”（常通过分解或扩充以特殊化、熟悉化）；③把“几何结论”转化为“代数、三角目标”，进一步明确立体几何转化思想和策略。还可通过对立体几何教学中的概念类比、方法类比的小结，提炼立体几何的类比思想和方法。

四、加强解题教学，突出思想方法指导

波利亚曾强调指出：“中学数学教学的首要任务就是加强解题训练”，然而他所大力倡导的“解题”完全不同于“题海战术”。他所提出的“怎样解题”表只是“题海游泳术”纲领，他认为解题应作为培养学生的数学才能和教会他们思考的一种手段和途径。因而，加强解题教学，不是搞题型训练，更不是搞题海，一方面通过解题和反思活动，在解题术的基础上总结归纳出解题方法，并提炼上升到思想高度；另一方面在解题活动中，应充分发挥数学思想，对发现解题途径的定向、联想和转化功能，突出它对解题指导作用。为此，在解题教学中，教师要善于通过选择典型例题进行解题示范，并且在解题过程中善于引导学生开展反思活动，突出数学思想方法对解题的统摄和指导作用。

参考文献

肖伯荣《数学思想方法及其教学示例》 江苏教育出版社2000.9