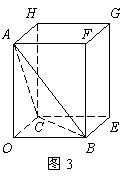
由正四面体的性质，运用联想类比的思想方法来探求直角四面体的性质。所谓直角四面体就是有一个三面角的各个面角都是直角的四面体。如图，四面体OABC在点O处的三个面角都是直角。所以四面体OABC是直角四面体。
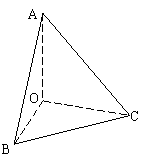
直角四面体的性质：
① 直角四面体的对棱互相垂直.
证明：如图
OB ⊥ OC，OB ⊥ OA。
OB ⊥ 平面OAC， 又
，同理可得: 
直角四面体的对棱互相垂直.
② 二面角A-OB-C、二面角A-OC-B、二面角B-OA-C都是直二面角.
证明：由（1）得OB ⊥ 平面OAC，
∠AOC是二面角A-OB-C的平面角，即二面角A-OB-C是直二面角。
同理可得:OC ⊥ 平面OAB，二面角A-OC-B是直二面角，
OD ⊥ 平面OBC，二面角B-OA-C是直二面角。
③ 直角顶点O在底面上的射影H是△ABC的垂心.
证明：连结
，并延长交
于
，连结
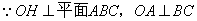
由三垂线定理的逆定理得 
同理，
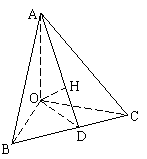
④ S2△BOC=S△BHC·S△ABC
证明： 
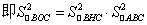
⑤ 
.
证明：
即 
同理，在
⑥ 不含直角的底面ABC是锐角三角形.
证明：设OA = a，OB = b，OC = c，则
，
，
，
在
中，由余弦定理得
，
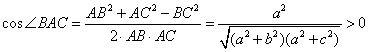所以∠BAC是锐角.同理可得∠ABC、∠ACB是锐角，所以△ABC是锐角三角形.
⑦ S2△BOC+S2△△AOB+S2△AOC=S2△ABC（底面面积S△ABC=
）
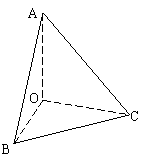
证明：由（6）得：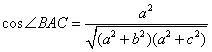 
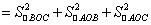
⑧ 体积 V=
.
证明： 
⑨ 外接球半径 R=
.
如图所示，以点O为长方体的一个顶点，OA、OB、OC为长方体的三棱作长方体OBEC-AFGH，则四面体OABC的外接球也是长方体OBEC-AFGH的外接球.设四面体OABC的外接球半径是R，则
.
⑩ 内切球半径r=
设△OAB的面积是S1，△OAC的面积是S2，△OBC的面积是S3，△ABC的面积是S4，则
， 
， 
，
由⑦得: 
.
由等体积原理得: 
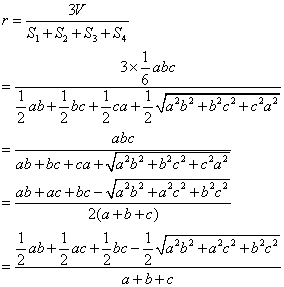
所以,内切球半径 r=
本文探究了直角四面体的一些有趣、优美的特性。在以后的学习中我们要学会挖掘一些特殊几何体的性质，以拓宽我们的数学思维。