立体几何（A版）中平行信息的处理方法

一 我们来看平行信息的一些重要特点

1．过已知直线外的一点作已知直线的平行线有且只有一条；过已知平面外的一点作已知平面的平行平面有且只有一个；过已知平面外的一点作已知平面的平行线有无数条，且它们都在同一个平面内；过已知直线外的一点作已知直线的平行平面有无数个，且都经过过已知点且和已知直线平行的直线。由此可见,在已知线（面）外一点作已知线（面）的平行线（面）时，要求是线线平行、面面平行的不同于要求是线面平行的，前者具有唯一性，而后者具有随意性。

2．线线平行、面面平行的传递性 ，传递性指的是两层含义

（1） 平行的自传递性：a∥b,b∥cc∥a及∥，∥ ∥

（2） 传递垂直信息及角的信息：

　　　①a∥b，　

　　　②∥，

　　　③a∥b，

　　　④∥，

　　　⑤a∥ba和c所成的角=b和c所成的角

　　　⑥a∥ba和平面所成的角=b和平面所成的角

　　　⑦∥，和斜交和所成的锐二面角=和所成的锐二面角

　　　⑧∥b和所成的角=b和所成的角

3. 线线平行在任何直观图中仍保持了平行特点，且是初中几何和高中几何的衔接点

我们知道一般用斜二测画法来画空间图形的平面图形，这和空间图形的真实形状是大不同的，但线线平行特征不比其它几何特征，它在直观图仍能保持，这非常难得，对我们研究立体几何有很大好处。

4．线线平行、线面平行、面面平行中的任何两种在一定条件下都可以相互转化

二 转化出平行信息的常用方法

方法1：要重视由平面图形中的信息转化出线线平行。如利用三角形的中位线转化出线线平行等。

方法2：用好线线平行、线面平行、面面平行之间的转化。将线面平行、面面平行转化成线线平行时要重视作好两平面的交线。

方法3：用垂直于同一个平面的两条直线平行来转化出平行线。

例1（2004年湖南高考·理工第19题）如图1，在底面是菱形的四棱锥P—ABCＤ中，∠ABC=600，PA=AC=a，PB=PD=,点E在PD上，且PE:ED=2:1，在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论.

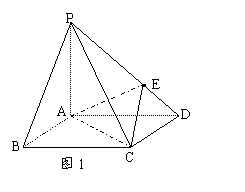
分析：此题作为题目的第三问,为了有效考查学生的思维，出题者将第三问设计成了探索的问题，此题若采用向量的方法或坐标的方法虽然也能做的出来，但是较费时，若能合理地分析平行信息，则可以有更好的方法。

方法1：可以先来思考能否过B作平面∥平面EAC，再研究作出的平面与棱PC的关系，当然要先考虑能不能过B作一条直线和平面EAC内的一条直线平行，在图2中设O为AC、BD的交点，不难发现平面EAC内的EO的这条线和BD相交，过B作EO的平行线比较合理。考虑到O为BD的中点，点E在PD上，且PE:ED=2:1，故只须取PD的另一个三等分点Q，即可得BQ∥EO，此时再取F为PC的中点，则有QF与平面EAC内的EC平行，从而平面EAC∥平面BQF，当然有F为棱PC的中点时，BF∥平面EAC。

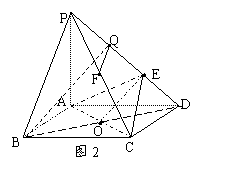
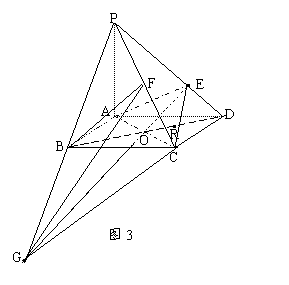
方法2：若能注意到所研究的问题与平面BPC与平面EAC的交线有关，则也可顺利得到思路。由于C为平面BPC与平面EAC的一个公共点，故还须再找一个公共点，在图3中，注意到平面BPC内的直线BP与平面EAC的直线EO一定相交，设交点为G，则平面BPC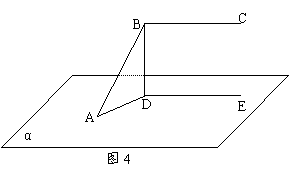平面EAC=CG，取R为BD的靠近D的三等分点，从而ER=BG，又，故BG=BP，在△PGC中取F为棱PC的中点时有BF//GC，从而BF∥平面EAC。

例2　如图4，直角∠ABC的一条边与平面斜交 ，另一条边BC不在平面内，∠ABC在上的射影仍是直角，求证：BC//

分析：此题关键在于如何用好垂直信息来产生平行。设B点在上的射影为D，设C点在上的射影为E，则AB的射影为AD，BC的射影为DE，依题意，∠ADE=，故先用三垂线定理大豆可得，结合， 可得BC⊥平面ABD，从而BC⊥BD，由于BD⊥DE，且B、D、E、C四点共面，故BD∥CE，从而BC//。

三 平行信息的一些重要应用

除了要重视将线线平行、线面平行、面面平行之间相互转化以及用好线线平行、面面平行的传递性外，还要重视以下两个方面的应用：

第一 用平行信息将求的角或距离的位置优化。

关于角前面已谈到，对于距离，以点到平面的距离为例，经常有这种情况，题中容易求出A点到平面的距离，但要求的是B点到平面的距离，此时一般要连结AB，若AB∥，则A点到平面的距离=B点到平面的距离；若直线AB和平面相交，设交点为O，若OA：OB能求出，此时可过B作（为A在平面内的射影）的平行线（为平行线与平面的交点），则，且A点到平面的距离：B点到平面的距离=OA：OB。

例3　如图5，已知正四棱锥P-ABCD的底面边长和各侧棱长均为13，M、N分别为PA、BC上的点，且PA：MA=BN：ND=5：8（1）求证：MN∥平面PBC（2）求直线MN和平面ABCD所成的角。

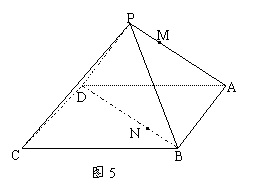
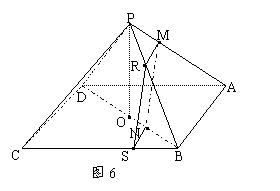
分析：考虑题中出现的比例线段（但比例线段不共面），应通过构造共面的比例线段自然而然作出在面PBC内与MN平行的直线，在图6中取R、S分别为PB、BC上的点，且PR：RB=BS：CS=5：8，故MR∥AB，MR=AB；NS∥CD且NS=CD。再结合AB∥CD，从而MR∥NS且 MR=NS，故MN∥RS，不难证MN∥平面PBC。对于第二问，值得考虑是原位置上求MN和平面ABCD所成的角，还是改到RS（由于RS∥MN）位置上求与面ABCD所成的角呢？显然RS在表面上，且RS的长度比较好求，.故将研究的角的位置放在RS比较好。设O为底面ABCD的中心，过R作RH∥PO交底面ABCD于H ，则RH⊥面ABCD，RH=PO=，此时不难有所求的直线MN和平面ABCD所成的角为。

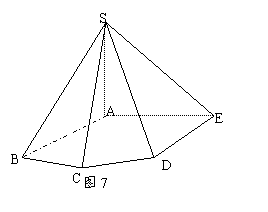
例4　（2005高考江苏卷）如图7，在五棱锥S－ABCDE中，SA⊥底面ABCDE，SA=AB=AE=2,BC=DE=,∠BAE=∠BCD=∠CDE=120°.

（Ⅰ）求异面直线CD与SB所成的角（用反三角函数值表示）；（Ⅱ）证明BC⊥平面SAB；（Ⅲ）用反三角函数值表示二面角B-SC-D的大小（本小问不必写出解答过程）

对第三问的分析：此题在第一问的解题过程中可证得底面ABCDE满足BE∥CD，从而在等腰梯形BCDE中不难有CD=，对于第三问，虽然不要解题过程，但如果方法不当将会计算量很大，甚至不能够完成。合理的解题思路可如下建立：如图8，由于巳证得BC⊥平面SAB，故面SAB⊥面SBC，且交线为SB，在面ABC内作AF⊥SB交CB于F ，则AF⊥面SBC，不难有AF=，此时可考虑过D作AF的平行线。连结AD，设直线AD交直线BC于P 点，则AD交平面SBC于P ，下面先来求DP：AP，在Rt△ABP中，过D 作DQ⊥BP，垂足为Q，则AB∥DQ且DQ=CD，故DP：AP=DQ：AB=3：4，连结PF，过D 作DH∥AF交PF于H，则DH⊥平面SBC，且不难有DH=，H在面SBC的反向延长面内（画Rt△BFP的真实图形可知）。在等腰三角形SCD中，SC=SD=，由面积法不难得腰SC上的高DK为，故二面角B-SC-D的平面角的正弦值为，从而二面角的大小为。

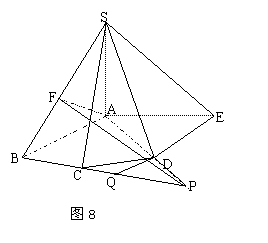
点评：此方法在求出A点到面SBC的距离基础上合理求出D点到面SBC的距离，从而有了较佳的计算量。

第二 在一定条件下将对面（线）面垂直的寻求转化为对平行线的寻求。

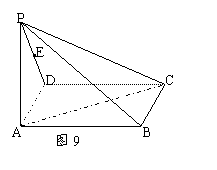
例5(2005湖北卷20) 如图9，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点. 在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离.

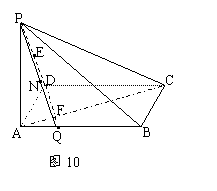
分析：如图10，根据题意要找出面PAC的垂线NE，应注意到面PAC内直线PA⊥面ABCD，故面PAC⊥面ABCD，且交线AC，因此在面ABCD内过D作DF⊥AC交AC于F, 交AB于Q，则可得DQ⊥面PAC，故要作的垂线问题即可转化为在侧面PAB内找一点N, 使EN∥DQ, 由于E为PD的中点,取N 为PQ的中点即可使EN∥DQ。在Rt△ADC中，利用射影定理可得FC=3AF，故AQ=DC=AB，从而有N点到AP的距离，N点到AB的距离为=1.

通过以上对平行信息可知,用好平行信息对解立体问题是非常重要的，对平行信息进行合理地分析也是很有必要的。