数学是研究现实世界的空间形式和数量关系的科学。数学中两大研究对象“数”与 “形”的矛盾统一是数学发展的内在因素,数形结合贯穿于数学发展中的一条主线,使数学在实践中的应用更加广泛和深远。一方面,借助于图形的性质将许多抽象的数学概念和数量关系形象化、简单化,给人以直观感;另一方面,将图形问题转化为代数问题,可以获得准确的结论。“数”与“形”的信息转换,相互渗透,不仅使解题简捷明快,还开拓解题思路,为研究和探求数学问题开辟了一条重要的途径。数形结合是连接“数”与“形”的“桥”,它不仅作为一种解题方法,还是一种重要的数学思想。
1.“数”“形”结合是推动数学发展
(1)“形”的问题可使用“数”来计算,“数”的关系可以用“形”来表现。
例如解析几何中将几何问题代数化,如关于直线斜率、距离、线段定比分点等等,将“代数”与“几何”相结合起来。
(2)“形”促进了“数”的概念的发展,丰富了计算方法。
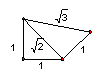
例如无理数的计算,例如![]() 、
、![]() 的发现,由边长为1的直角三角形得。
的发现,由边长为1的直角三角形得。
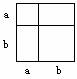
代数恒等式![]() 的证明如图。
的证明如图。
2.数形结合在教学中的运用
数形结合渗透在中学数学中,数形结合的观点是通过对数量关系的讨论来研究图形的性质,也可利用图形的性质来反映数量间的相互关系,因此数形结合使数和形相互启发、相互补充、相互印证。
初中代数中就有意识地渗透数形结合的思想和方法。如数轴就是把数和形结合在一起,数轴把点与数的对应关系揭示出来,这样数量关系常常可以通过几何图形做出直观地反映和描述。
如:相反数就是在原点两旁到原点距离相等的两个点所表示的数。零的相反数是它本身即原点。如图:
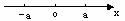
绝对值表示这个数的点与原点的距离。利用数轴可以准确、快速地确定结论,在下图中,A点到原点的距离比B点到原点的距离大。
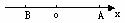
高中数学中,数和形结合的思想更是贯穿始终。如在讲函数概念、用文氏图表示集合的关系;用数轴表示定义域、值域等都体现了几何思想;在三角函数、复数、微积分等中,也利用数形结合,帮助我们更快、更好地解决问题,更容易、更轻松的突破重、难点。 在平面、空间解析几何……,体现了代数的思想。简而言之,代数教学中充满了几何的思想,几何教学中蕴涵着代数的思想。
3.数形结合在解题中的运用
作为解题方法,“数形结合”实际上包含两方面:一面是“形”的问题,引入直角坐标系,寻找其数量关系式,用“代数”来解决;另一面对代数问题,分析其几何意义,借助“形”的直观来解答。
(1) “数”中思“形”
例1. 如果实数![]() 满足方程
满足方程![]() ,求
,求![]() 的最大值。
的最大值。
解:不妨设点![]() 在圆
在圆![]() 上,圆心为
上,圆心为![]() ,半径等于
,半径等于![]() (如图)则
(如图)则![]() 是点
是点![]() 与原点连线的斜率。当
与原点连线的斜率。当![]() 与⊙
与⊙![]() 相切,且切点
相切,且切点![]() 落在第一象限时,
落在第一象限时,![]() 有最大值,即
有最大值,即![]() 有最大值。
有最大值。
因为![]() =
=![]() ,
,![]() =
=![]() ,所以
,所以![]() =
=![]() =
=![]() ,
,
所以![]() =
=![]() =
=![]() 。
。

例2. 解不等式:![]()
解: 设![]() ,即
,即![]() 对应的曲线是以
对应的曲线是以![]() (
(![]() ,0)为顶点,开口向右的抛物线的上半支。而函数
,0)为顶点,开口向右的抛物线的上半支。而函数![]() 的图象是一直线。解方程可求出抛物线上半支与直线交点的横坐标为2,此不等式的解在图象上就是抛物线位于直线上方的部分,故不等式的解集是
的图象是一直线。解方程可求出抛物线上半支与直线交点的横坐标为2,此不等式的解在图象上就是抛物线位于直线上方的部分,故不等式的解集是![]() 。
。
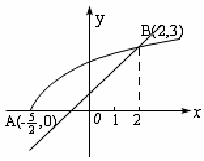
例3.方程![]() ,
,![]() 的解分别是
的解分别是![]() ,求
,求![]()
解:求上方程的解比较困难,方程![]() 的解,可理解为函数
的解,可理解为函数![]() 与
与![]() 的交点(B点)横坐标,方程
的交点(B点)横坐标,方程![]() 的解为函数
的解为函数![]() 与
与![]() 的交点(A点)的横坐标,函数
的交点(A点)的横坐标,函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称, A、B关于直线
对称, A、B关于直线![]() 对称,直线
对称,直线![]() 与
与![]() 的交点为C点,所以A、B点关于C点对称,C点横坐标是
的交点为C点,所以A、B点关于C点对称,C点横坐标是![]() ,所以
,所以![]()
(2)“形”中觅“数”
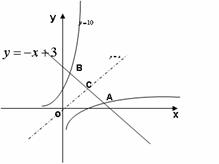
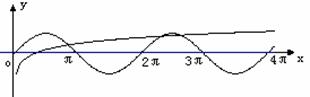
例4.求方程![]() 的解的个数。
的解的个数。
分析:此方程解个数即函数![]() 的图象与函数
的图象与函数![]() 图象的交点个数。
图象的交点个数。
因为![]() ,
,![]() ,所以
,所以![]() 在平面直角坐标系中作出两个函数的图象,如图,形中觅数,可直观地看出两曲线有3个交点。
在平面直角坐标系中作出两个函数的图象,如图,形中觅数,可直观地看出两曲线有3个交点。
例5.已知复数![]() 满足
满足![]() =
=![]() π ,求
π ,求![]() 的最大值。
的最大值。
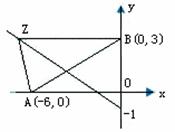
解:要求![]() 的最大值,即求
的最大值,即求![]() 的最小值,由复数模的几何意义知即求复数
的最小值,由复数模的几何意义知即求复数![]() 对应的点到点
对应的点到点![]() 和点
和点![]() 的距离和的最小值。如图
的距离和的最小值。如图
∵ ![]() 满足
满足![]() =
=![]() π
π
∴复数![]() 对应的复平面上的点
对应的复平面上的点![]() 的轨迹是以
的轨迹是以![]() 为端点,倾斜角为
为端点,倾斜角为![]() 的射线。由图可知,
的射线。由图可知,![]() 最小值为
最小值为![]() =
=![]() =
=![]() ,故
,故![]() 的最大值是
的最大值是![]() =
=![]() 。
。
在数形转化过程中,必须遵循等价转换原则、数形互补原则。当然在教学渗透数形结合的思想时,应注意培养以下几点:
1. 观察图形,找出图形中蕴含的数量关系。
2. 正确绘制图形,反映图形中相应的数量关系。
3. 切实把握“数”与“形”的对应关系,以图识性,以性识图。
总而言之,“数无形不直观,形无数难入微” 。见到数量就要考虑它的几何意义,见到图形就应考虑它的代数关系,运用数形结合的思想解决数学问题。因此数形结合思想在中学数教学中起着举足轻重的作用。