摘 要:兴趣是推动学生学习的一种最实际的内部动力,直接影响学习的效果。所以,培养学生的数学学习兴趣,是数学教学的重要内容之一。本文从分析中学生厌恶数学的原因入手,针对其原因及学生的喜好,提出了“通过创设美好的数学问题情境教学,培养和发展学生的学习兴趣”的观点。所谓创设问题情境是以问题为载体,创设与教学目标、内容,学生认知结构紧密相关的问题。文中详细介绍了创设问题情境的几种主要方式,并通过一定的教学案例,对每种创设方式进行了辅助说明,随后通过对创设问题情境的主要方式的论述,指明了创设问题情境的原则。创设问题情境,不仅能够激发学生的学习兴趣,而且能够培养学生自主地探索,解决问题的能力。
关键词:中学生厌学的原因、创设问题情境的主要方式、创设问题情境的原则
引言
德国教育学家第斯多惠指出:“数学的艺术不在于传授本领,而在于激励、唤醒、鼓舞。”一节课中,有的学生学的主动活泼、津津有味,有的学生精神不振,昏昏欲睡,这种现象归根到底是兴趣问题。《中学数学教学大纲》指出:“要培养学生对数学的兴趣,激励学生为实现四个现代化学好数学的积极性”。兴趣是人对客观事物的选择性态度,它表现为人力求认识和获得某种事物,并且力求参与相应的活动。兴趣通过情绪反应来影响一个人的行为积极性,即凡是从事自己感兴趣的学习和工作,人就会觉得心情舒畅和愉快,效率也较高。相反,如果是从事自己不感兴趣的事,则可能心理动力不够,缺乏激情,效率也就较低。对于中学生来说,他们的学习在很大程度上要受兴趣和情绪的左右,因此,培养学生学习的兴趣,有助于提高学生的学习积极性,从而增进其学习的效率。因而,教师在数学教学过程中要了解学生不喜欢数学的原因,并要善于挖掘教材潜力,创设美好的数学情境教学,以便激励、唤醒、鼓舞学生,激发学生饱满的学习热情,促使他们以积极的态度和旺盛的精力主动求索,从而获得最佳效果。
1 中学生厌学的原因
有人在2001年“中学生学习数学的兴趣调查”中发现学生对数学的喜欢程度已经表现出明显的分化,表示“喜欢”,“一般”和“不喜欢”的比率各占“24.9%”,“60.4%”,“14.7%”,学生对数学感兴趣的原因29%以上是因为数学知识与生活实际密切相关,12.3%是因为喜欢它的逻辑推理性强,10%受教师的讲课质量的影响等。
不喜欢的原因有:
──数学的抽象性和严谨性,教学中过早地训练,使学生产生对数学单调和枯燥的感觉。
──对数学的意义和数学的价值认识不足,并认为数学远离生活,它的用处和目的存在距离。
──学生本身性格差异,如喜欢数学、文学、体育、文艺等……,个人价值观不同。
──学生基础差,一直学不好,缺乏成功的感受与体验。
──学生不断碰到困难,遇到挫折,害怕学,甚至讨厌数学。
──“精英教育”“应试教育”的弊端,导致考试无望的学生对数学厌倦,对数学失望。
──社会对数学人才不重视,和对人的数学素质的冷漠产生的负作用。
──教师教法陈旧,及师道尊严的课堂文化,使学生对数学兴趣渐减。
──理论与实际联系不够,使学生对学习数学的目的感到茫然。
──学生个人、家庭、环境的一些变化,引起学生数学兴趣的波动。
2 通过创设美好的数学问题情境教学,培养和发展学生的学习兴趣
思维始于问题,问题是思维的出发点,是数学的生命,没有问题数学就失去了魅力。对于学生来说,提出一些他们想解决而未解决的、富有挑战性的、趣味性的问题,出现美好的数学问题情境,更能激发学生学习数学的兴趣和内向力,促使他们积极思考,生动活泼的学习。
2.1 创设问题情境的主要方式
2.1.1 创设应用性问题情境,引导学生自己发现数学命题(公理、定理、性质、公式)
数学应用性问题能调节人们的心理倾向,激发兴趣,培养学生追溯问题的背景和原型,使其思维发散、个性发展,形成分析问题和解决问题的能力,提高数学应用能力,这是数学素质教育的要求,是时代的要求,解决数学应用性问题的过程是运用数学知识、数学思想、数学方法分析研究客观世界的种种现象,并加工整理和组织的过程,也是密切联系实际,从实际中建立数学概念、模型,形成数学思想的过程。教学中,教师可以通过创设应用性问题的情境,展示这一过程。 数学的高度抽象性常常使学生误认为数学是脱离实际的,其严谨的逻辑形式使学生缩手缩脚,其应用的广泛性更使学生觉得高深莫测,望而生畏。在教学过程中,教师可利用数学与实际问题的联系来创设应用性问题情境,把抽象问题具体化。
【案例1】在“均值不等式”一节的教学中,可设计如下两个实际应用问题,引导学生从中发现关于均值不等式的定理及其推论。
①某商店在节前进行商品降价酬宾销售活动,拟分两次降价。有三种降价方案:甲方案是第一次打![]() 折销售,第二次打
折销售,第二次打![]() 折销售;乙方案是第一次打
折销售;乙方案是第一次打![]() 折销售,第二次打
折销售,第二次打![]() 折销售;丙方案是两次都打
折销售;丙方案是两次都打![]() 折销售。请问:哪一种方案降价较多?
折销售。请问:哪一种方案降价较多?
②今有一台天平两臂之长略有差异,其他均精确.有人要用它称量物体的重量,只须将物体放在左、右两个托盘中各称一次,再将称量结果相加后除以2就是物体的真实重量。你认为这种做法对不对?如果不对的话,你能否找到一种用这台天平称量物体重量的正确方法?
学生通过审题、分析、讨论,对于问题①,大都能归结为比较![]() 与
与![]() 大小的问题,进而用特殊值法猜测出
大小的问题,进而用特殊值法猜测出![]() ≤
≤![]() ,即可得
,即可得![]() ≥
≥![]() .
.
对于问题②,可安排一名学生上台讲述:设物体真实重量为![]() ,天平两臂长分别为
,天平两臂长分别为![]() 、
、![]() ,两次称量结果分别为
,两次称量结果分别为![]() 、
、![]() ,由力矩平衡原理,得
,由力矩平衡原理,得![]() ,
,![]() ,两式相乘,得
,两式相乘,得![]() ,由问题①的结论知
,由问题①的结论知![]() ≤
≤![]() 即得
即得![]() ≥√
≥√![]() ,从而回答了实际问题.此时,给出均值不等式的两个定理,已是水到渠成,其证明过程完全可以由学生自己完成.
,从而回答了实际问题.此时,给出均值不等式的两个定理,已是水到渠成,其证明过程完全可以由学生自己完成.
以上两个应用问题,一个是经济生活中的问题,一个是物理中的问题,贴近生活,贴近实际,给学生创设了一个观察、联想、抽象、概括、数学化的过程.在这样的问题情境下,再注意给学生动手、动脑的空间和时间,学生一定会想学、乐学、主动学.
2.1.2 创设趣味性问题情境,引发学生自主学习的兴趣
趣味性的知识总能吸引人,特别是中学生,趣味性的内容可引发他们对问题的探究和深层次思考。教学中,教师可根据这一特点,设计有趣味性的问题情境,多为学生提一些数学史、数学家的故事或其他有趣的知识,即激发了学生的学习兴趣,又能扩大学生的知识面。
【案例2】在“等比数列”一节的教学时,可创设如下有趣的问题情境引入等比数列的概念。
阿基里斯(希腊神话中的善跑英雄)和乌龟赛跑,乌龟在前方1里处,阿基里斯的速度是乌龟的10倍,当它追到1里处时,乌龟前进了1/10里,当他追到1/10里,乌龟前进了1/100里;当他追到1/100里时,乌龟又前进了1/1000里……
①分别写出相同的各段时间里阿基里斯和乌龟各自所行的路程;
②阿基里斯能否追上乌龟?
让学生观察这两个数列的特点引出等比数列的定义,学生兴趣十分浓厚,很快就进入了主动学习的状态.
2.1.3 创设开放性问题情境,引导学生积极思考
开放性问题通常是改变结构,改变设问方式,增强问题的探索性以及思维的深刻性,对命题赋予新的解释进而形成和发现新的问题。由于它具有与传统封闭型不同的特点,因此在数学教学中有其特定的功能。数学开放性问题的教学为学生提供了更多的交流和合作的机会,为充分发挥学生的主体作用创造了条件。数学开放性问题的教学过程使学生主动构建,积极参与的过程,这一过程有利于培养学生数学意识,发展学生的数学感觉,真正学会“数学思维”。数学开放性问题的教学过程也是探索和创造的过程,它可以促进学生全面地观察问题,深入地思考问题,有利于学生自主学习能力的培养和探索、开拓、创造精神的培养。
【案例3】![]() ,
,![]() 是两个不同的平面,
是两个不同的平面,![]() ,
,![]() 是平面
是平面![]() 及
及![]() 之外的两条不同的直线,给出四个论断:①
之外的两条不同的直线,给出四个论断:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,以其中三个论断作为条件,余下一个论断作为结论,条件和结论都不是固定的,是可变的,解答该题需要数学去思考、分析、尝试、猜想、论证,既具探索性。
,以其中三个论断作为条件,余下一个论断作为结论,条件和结论都不是固定的,是可变的,解答该题需要数学去思考、分析、尝试、猜想、论证,既具探索性。
2.1.4 创设直观性图形情境,引导学生深刻理解数学概念
数学的抽象性往往使学生的思维受阻,如果能使抽象问题具体直观,就可以大大降低难度了。数形结合较好地解决了这一问题,通过数形结合,使学生对问题有了更深刻的理解和认识,同时也使学生对数学减少了恐惧,进而也增加了兴趣。
【案例4】圆和圆的位置关系,如果凭空说道理,学生是难以明白的,如果创设直观性图形情境,给出下图:(其中![]() 是圆心距,
是圆心距,![]() 是大圆半径,
是大圆半径,![]() 是小圆半径)
是小圆半径)
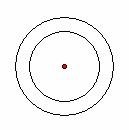
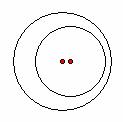
同 心 ![]() 内 含
内 含![]()
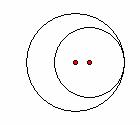
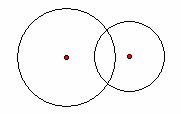
内 切![]() 相 交
相 交![]()
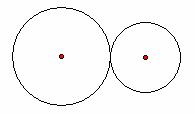
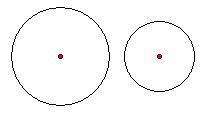
外 切![]() 相 离
相 离 ![]()
显然会给学生一个非常直观易懂的圆与圆的关系结构图。
2.1.5 创设新异悬念情境,引导学生自主探究
新颖的东西能激发人的兴趣,学生的学习兴趣常常是在丰富多彩、新异生动的教学内容中得到激发的,增强教学内容的新颖性,就是要使每节课的内容具有新意的知识,并提供不同的方式让学生掌握,尽量避免内容和形式上的单调和呆板,因此教师可创设以下情境:
【案例5】在“抛物线及其标准方程”一节的教学中,引出抛物线定义“平面上与一个定点![]() 和一条定直线
和一条定直线![]() 的距离相等的点的轨迹叫做抛物线”之后,设置这样的问题情境:初中已学过的一元二次函数的图象就是抛物线,而今定义的抛物线与初中已学的抛物线从字面上看不一致,它们之间一定有某种内在联系,你能找出这种内在的联系吗?
的距离相等的点的轨迹叫做抛物线”之后,设置这样的问题情境:初中已学过的一元二次函数的图象就是抛物线,而今定义的抛物线与初中已学的抛物线从字面上看不一致,它们之间一定有某种内在联系,你能找出这种内在的联系吗?
此问题问得新奇,问题的结论应该是肯定的,而课本中又无解释,这自然会引起学生探索其中奥秘的欲望.此时,教师注意点拨:我们应该由![]() 入手推导出曲线上的动点到某定点和某定直线的距离相等,即可导出形如动点
入手推导出曲线上的动点到某定点和某定直线的距离相等,即可导出形如动点![]() 到定点
到定点![]() 的距离等于动点
的距离等于动点![]() 到定直线
到定直线![]() 的距离.大家试试看!学生纷纷动笔变形、拼凑,教师巡视后可安排一学生板演并进行讲述:
的距离.大家试试看!学生纷纷动笔变形、拼凑,教师巡视后可安排一学生板演并进行讲述:
由![]() 得
得![]()
得 ![]() 得
得![]()
它表示平面上动点![]() 到定点
到定点![]() 的距离正好等于它到直线
的距离正好等于它到直线![]() 的距离,完全符合现在的定义.
的距离,完全符合现在的定义.
这个教学环节对训练学生的自主探究能力,无疑是非常珍贵的.
2.1.6 创设疑惑陷阱情境,引导学生主动参与讨论
由于学生原有认知结构与新知识之间产生矛盾,因此学习中经常会产生各种错误,教师可合理选用一些问题,通过设疑、激疑创设问题情境,帮助学生发现问题,引起学生的思考和钻研,有利于学生主动获取知识,主动开启知识宝库,提高发散思维能力。
【案例6】双曲线![]() 上一点
上一点![]() 到右焦点的距离是5,则下面结论正确的是( ).
到右焦点的距离是5,则下面结论正确的是( ).
A. ![]() 到左焦点的距离为8
到左焦点的距离为8
B. ![]() 到左焦点的距离为15
到左焦点的距离为15
C. ![]() 到左焦点的距离不确定
到左焦点的距离不确定
D. 这样的点![]() 不存在
不存在
在教学时,根据学生平时练习的反馈信息,有意识地出示如下两种错误解法:
错解1:设双曲线的左、右焦点分别为![]() 、
、![]() ,由双曲线的定义得:
,由双曲线的定义得:
![]() ∵
∵![]() ∴
∴![]() ,故正确的结论为B.
,故正确的结论为B.
错解2:设![]() 为双曲线右支上一点,则
为双曲线右支上一点,则![]() ,
,
由![]() ,
,![]() , 得
, 得 ![]() ∴
∴ ![]() ,故正确结论为B.
,故正确结论为B.
然后引导学生进行讨论辨析:
若 ![]() ,
, ![]() ,则
,则 ![]() ,
,
而 ![]() ,即有
,即有 ![]() ,
,
这与三角形两边之和大于第三边矛盾,可见这样的点![]() 是不存在的.因此,正确的结论应为D.
是不存在的.因此,正确的结论应为D.
进行上述引导,让学生比较定义,找出产生错误的原因,即是忽视了双曲线定义中的限制条件,所以除了考虑条件![]() , 还要注意条件
, 还要注意条件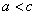 和
和![]() ≥
≥![]() .
.
通过上述问题的辨析,不仅使学生从"陷阱"中跳出来,增强了防御"陷阱"的经验,更主要地是能使学生参与讨论,在讨论中自觉地辨析正误,取得学习的主动权.
2.1.7 从同一问题通过不同推理和运算,产生形式上不同的结果,设置问题情境
【案例7】分解因式:![]() 学生有两种解法,出现两种不同结果:
学生有两种解法,出现两种不同结果:
![]()
![]()
比较这两种结果,教师提出问题:为什么有两种不同结果?是不是其中一个等式不成立?在排除了“其中一个等式不成立”的想法后,进一步提出猜想:![]()
从而设置“![]() 能不能分解因式?如何分解?”的问题情境。
能不能分解因式?如何分解?”的问题情境。
2.1.8 创设已有知识的问题序列,引导学生自己获取新知识的生长点
【案例8】在“曲线和方程”的教学中,对于“曲线的方程”和“方程的曲线”概念的引入,可利用函数图象设计如下问题序列:①下列各图中哪些能作为函数图象?(无解析式)②如何修改可作为函数的图象?③再添上图下的解析式,并问:图与式相一致吗?请改图形(或改关系式)使两者相吻合.④既然图象与解析式存在着这种对应的关系,怎样反映这种关系呢?
至此,学生对“曲线”与“方程”的关系已有了一些初步的认识,在此基础上指导学生阅读课本,学生就能够理解曲线和方程的“纯粹性”及“完备性”的含义,也就理解了什么是“曲线的方程”和“方程的曲线”。
2.1.9 创设题组问题情境,引导学生创新发现
在数学教学中,根据学生的认知规律,合理有效地选用一组数学问题组织教学,并且在这些问题的解决过程中,除了解决个别数学问题的方法的变化,形成一种更高层次的思维方法,以达到对问题本质的了解、问题的难点的突破、问题规律的掌握、知识技能的巩固、思维的拓展和迁移等目的,这种题组并不是几个独立数学问题的简单组合,而是注重题目之间的内在联系,使它们的解决能启示某些问题的规律,能引导与启发学生掌握这些规律。
【案例9】在不等式证明中给出了这样一组题:已知:![]()
①求证:![]() ≥
≥ ![]()
②求证: ![]() ≥3
≥3
③求证: ![]() ≥3
≥3
第①问除了学生能用![]() ≥
≥![]() 的方法证明之外,还可引导学生用
的方法证明之外,还可引导学生用![]() ≥
≥![]() 。构造“倒数”关系来证。有了证法2之后,通过类比,学生很容易解决②但在继续解决③的过程中,遇到了困难,引导学生将③与①,②对比联系,学生立即发现:构造上很相似,③不能处理的原因是分母是多项式无法直接做除法构造“倒数”关系,怎么办?找到问题的症结之后,立即有一部分观察能力较强的同学创造性地发现用换元的手段将分母变成单项式不就解决了吗?通过类比,有了下面的创造性解法。设
。构造“倒数”关系来证。有了证法2之后,通过类比,学生很容易解决②但在继续解决③的过程中,遇到了困难,引导学生将③与①,②对比联系,学生立即发现:构造上很相似,③不能处理的原因是分母是多项式无法直接做除法构造“倒数”关系,怎么办?找到问题的症结之后,立即有一部分观察能力较强的同学创造性地发现用换元的手段将分母变成单项式不就解决了吗?通过类比,有了下面的创造性解法。设![]() ,则
,则![]() , 下面完全可以由学生独立完成。
, 下面完全可以由学生独立完成。
题组教学确有其独特的作用,能有效地培养学生的归纳能力和分析问题解决问题的能力。在教学中教师要适当地运用题组教学,降低教学难度,减少学生解题的盲目性,使学生感到数学问题是很有趣的,充分拓展学生的思维,以达到更好的教学效果。
2.1.10 创设实验性问题情境,引导学生发现规律
当学生的原有认知结构中已经具有学习新知识的预备知识,但新旧知识之间的逻辑联系还不容易被学生发现时,教师可以通过具体实验设置问题情境,让学生通过观察、画图、动手等实践活动,探索规律,提出猜想,然后通过逻辑论证得到定理和公式。
【案例10】在教“不在一条直线上的三点确定一个圆”时,教师先发给每一个学生一张破碎了的圆形硬纸片,并且说“机器上的皮带轮碎了,为了再制造一个同样大小的皮带轮,请你设法画出皮带轮对应的圆形。”接着让学生用圆规、直尺、量角器等比比画画,进行实验,探索问题的解法。然后在实验的基础上,设置问题情境:过不在一条直线上的三点可以画几个圆?
【案例11】在讲“数学归纳法”时,由于数学归纳法比较抽象,许多学生对“一个与自然数有关的命题经过数学归纳法的步骤证明后是正确的”不太理解,特别是对它为什么要有第二步不理解,因此可通过设置试验情境:“多米诺”骨牌游戏:几十个骨牌一个紧挨着一个放在桌上,排列成弯弯曲曲的蛇形队列,用一只手指推到第1个骨牌,紧接着第2个骨牌、第3个骨牌……依次都倒下。可以清楚地看到,要使每一个骨牌都倒下,除了第1个骨牌必须倒下以外,还必须有:如果前面一个骨牌倒下,那么后面一个骨牌就紧接着倒下。也就是必须要有当![]() 成立时,
成立时,![]() 也成立。
也成立。
2.1.11 创设问题情境,引导学生精读教材,提高学生自主学习的能力
引导学生自学,是培养自主能力的重要途径。对于新教材,必须采用新的教学策略。在教学中,首先要让学生观察书中“章头图”,通过观察展开丰富的联想,进而阅读注重设计的探索性思考题,激发学生追求新知的欲望,对于每一节的内容,可设计系列问题,促使学生带着问题自觉地阅读教材。
【案例12】讲《集合》一节。可设计如下问题:
① 如何理解概念中的“指定”两字?
② 概念中的“对象”可以是一些什么东西?
③ 常用的数集有哪些?分别用什么字母表示?
④ 集合元素之间存在着什么关系?
⑤ 集合中的元素具有哪些特征?如何解释这些特征?
引导学生带着问题阅读教材,能激发学生积极主动的思维,加深学生对概念的理解,培养学生的自主学习能力。
2.1.12 利用对数学美的鉴别、比较来创设问题情境,以促使学生发现数学美
数学以其简洁性、对称性、和谐性、统一性、奇异性为特征表现出它的美。数学美是一种理想的美,抽象的美,没有一定数学素养的人,不可能感受数学美,更不能发现数学美。教师可在课堂上设置各种情境展示数学美,培养学生欣赏数学的美学价值,使他们喜欢数学,热爱数学。
【案例13】在解析几何中,推导点![]() 到直线
到直线![]() 的距离公式,教师可以如此安排教学:
的距离公式,教师可以如此安排教学:
先求出点![]() 到直线
到直线![]() 的距离
的距离![]() ;
;
再求出点![]() 到直线
到直线![]() 的距离
的距离![]() ;
;
在此基础上,引导学生观察,猜测求出点![]() 到直线
到直线![]() 的距离形式
的距离形式![]() 。
。
对分母?,可以为学生提供这些选项:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 。结果表明大部分学生学选择了
。结果表明大部分学生学选择了![]() 。因为
。因为![]() 或
或![]() 不全面,
不全面,![]() 较松散,
较松散,![]() 次数不统一。这些说法看起来“没道理”,但它恰恰是学生凭直觉所得的结果,从某种意义上讲,分母
次数不统一。这些说法看起来“没道理”,但它恰恰是学生凭直觉所得的结果,从某种意义上讲,分母![]() 恰恰体现公式结构美。
恰恰体现公式结构美。
2.1.13 利用解题后的反思创设问题情境,巩固学生自主学习的意识
解题者提出了数学题的答案,并不意味着解题思维活动的结束,而是深入认识的开始。解题反思是对解题活动的反思,它是对解题活动的深层次的思考;是不断调整思维结构,深化思维层次,提高思维水平的过程;是进一步开发解题智力的过程;是一种再发现和再创造的过程。解题反思贯穿解题学习的全过程,也是对解题的原认知过程,如果学生在每一次解题之后都能对自己的思路作自我评价,探讨成功的经验和失败的教训,对解题过程中反映的数学思想方法进行总结、概括,这样长此以往,不仅能巩固知识,避免解题的错误,而且可以把解决问题的数学思想方法及对问题的再认识转化为一个学习过程,更提高学生分析问题、解决问题的能力,优化他们的数学思维,达到融会贯通的境界。在教学中,教师要引导学生通过对解题的反思来创设问题情境。
【案例14】已知![]() ,求证:
,求证:![]() ≥
≥![]() 。
。
在证明了这个问题之后,引导学生对解题过程反思可创设如下问题:
①已知![]() ,求证:
,求证:![]() ≥
≥![]() 。
。
②已知![]() ,你能猜想
,你能猜想![]() 不小于什么吗?如何证明呢?
不小于什么吗?如何证明呢?
2.2 创设问题情境的原则
创设情境的方法很多,但必须做到科学、适度,具体地说,有以下几个原则:
① 问题要具体明确。这是问题情境设计最基本的原则。提出的问题必须目的明确,紧紧围绕教学目标,而且要非常具体,即表达简明扼要和清晰,不要含糊不清,使学生盲目应付,思维混乱。这样学生能理解问题的含义,才有可能来探索、思考和解决这些问题。
② 问题要有新意。为了激发学生的求知欲望,提高学生学习的兴趣,在设置问题情境时,必须选择新颖的问题。
③ 问题要有启发性。教师在深入分析教学内容和学生情况的基础上,根据教学目标设计使学生的原有认知结构和新知识产生矛盾的富有挑战性的问题。
④ 问题要有适应性。考虑到学生的知识水平和智力要求,问题的深度、广度要适当既在学生力所能及的范围之内,又能激发学生的认知冲突。
⑤ 问题要少而精,做到教者提问少而精,学生质疑多且深。
⑥ 教师设计时要注意时机,情境的设置时间要恰当,寻求学生思维的最佳突破口。
结 论
创设问题情境是属于问题的发现,问题的提出和解决的重要手段和途径,对数学教学和数学学习尤其为重要,不仅能提高教学质量,也能提高学生素质,关键在于能充分调动全体学生的学习兴趣,学习积极性,能促进学生主动发展。创设应用性问题情境,理论联系实际,不仅把抽象问题具体化,学生容易接受,而且可以使学生认识到数学与生活紧密相关,并非远离生活,就会引起学生对数学的学习兴趣;创设趣味性问题情境和创设新异问题情境,可以避免数学的枯燥性和单调性,使学生感觉数学是有趣的;创设开放性问题情境,可以促进学生全面地观察问题,深入地思考问题,并用科学思想方法去探索、发现、归纳数学问题;创设直观性图形情境,直观的东西更能引起学生的注意力和兴趣,通过数形结合,可以降低问题的难度,减少学生对数学的恐惧,使学生对问题有更深刻的理解和认识;创设疑惑陷阱情境,可以产生很好的师生互动的效果,让学生参与讨论,自己慢慢解决问题,能够培养学生的成就感,使学生勇于挑战数学;创设实验问题情境,可以降低教学内容的抽象性,使学生容易理解,让学生通过观察和动手操作,在实验的情境中提高分析和解决问题的能力。
总之,创设问题情境,不仅能够激发学生的学习兴趣,而且能够培养学生自主地探索,解决问题的能力。教师在数学教学过程中要了解学生不喜欢数学的原因,并要善于挖掘教材潜力,创设美好的数学情境教学,以便激励、唤醒、鼓舞学生,激发学生饱满的学习热情,促使他们以积极的态度和旺盛的精力主动求索,从而获得最佳效果。
参考文献
1 张惠民.例谈反例的构建.中学数学教学参考.2002/09
2 邵瑞珍.教育心理学.上海教育出版社.1997
3 罗增儒.中学数学课例分析.陕西师范大学出版社.2001/07
4 洪秀满.制约数学问题解决的心理因素.中学数学.2002/02
5 孙宏安,程晓红.现代数学设计.华东师范大学出版社.2003/04
6 奚定华.数学教学设计.华东师范大学出版社.2003/04
7 朱万成.浅谈对学生学习数学情感的培养.中学数学研究.2004/09
8 宋秉信.数学学习论.重庆大学出版社.1996/02