立体几何入门探讨

如何解决立体几何中的证明问题呢？

首先要对课本中的公理、定理、定义推论要有一个深刻中认识和理解，就是要弄明白这些命题究竟表达的是什么意思，弄清题设和结论。只要做好这一步，我们才可以灵活地应用这个定理。例如：高二数学教材第二册（下A），平面的基本性质公理2：如果两个平面有一个公共点，那么它们还有其他公共点，并且所有这些公共点的集合是一条过个公共点的直线。这个公理读起来会让人感觉很别扭，不是那么的顺畅，其实它有三层意思：（1）有一个公共点必存在其它公共点（2）有一个公共点，必有一条公共直线（3）有公共点，这些公共点都共线。显然只要深刻理解了这一公理，我们就可以依据这一公理轻松的解决点共线问题。

其次，要把课本中的定理牢记在心中，当然我要说明的不是要你把定理的语言文字牢记在心中，而是要把它的意思牢记在心中，一般来说这一过程需要多练题反复的巩固记忆。

以上两点是我们学好立体几何证明问题的必备条件。有了以上两点，我们来谈谈如何解决立体几何中的证明题：下面我着重从解决证明问题的三种思维模式出发来阐述这个问题，在这里我不妨叫它三步思维模式：

1、从结论出发寻求证明依据（依据一般定理、公理、推论)

2、从条件出发得出某些相关结论，建立结论与条件的联系，寻找所需要信息。

3、条件不足，创造条件，达到目的（创造条件一般就是作辅助线，构造特殊图形）

上述三点是我们解决几何问题的基本模式，牢固掌握好这三种思维模式是我们学好立体几何的根本出发点。

当然对于以上三点，我需做些补充说明：（1）对于要证明的结论转化为另一种形式加以证明（2）寻找所需信息就在多个条件存在下，寻求和本问题有联系的信息（3）条件不足，创造条件就是在条件与结论联系不够紧密，经过上述两种思维模式思考后，还难以达到目的的情况下，我们需要借助辅助线，构造一些特殊图形，以此建立条件与结论的联系。（4）后面所讲的定理一般指的是包含了公理、推论、定理等、命题，是广义上的定理。（5）这里第一、二步其实就是我们数学上的分析法和综合法，在这里我仅仅具体化而已。对于以上所述如果感到很抽象的话，下面我着重通过几个实例来直观阐述以上三步思维模式的应用。

实例1、在正方体ABCD-A₁B₁C₁D₁中，设A₁C与平面ABC₁D₁交于Q，

求证：B、Q、D₁共线

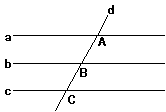
（1）由结论出发寻求证明依据。

欲证明B、Q、D₁共线，联想哪些定理涉及到共线问题，显然公理2描述的就是一个点共线问题，为此我们就会想到用公理2来证明本题结论。当然公理2所表达的条件是两个平面的公共点，那就是说要用公理2来证明共线，就需要证明这些点同时是哪两个平面的公共点。观察图形我们发现这些点可以是很多对平面的公共点。究竟该选哪两个平面呢？

（2）建立条件与结论的联系，寻求所需信息。

回到上面的问题，如何寻找这两个平面？我们来看看条件。题中条件给出了A₁C与平面ABC₁D₁交于Q。由此我们不妨着眼于A₁C所在平面以及平面ABC₁D₁，联系要证明的问题，我们就可以找到两个平面，即平面A₁BCD₁与平面ABC₁D₁，显然证明它们是平面A₁BCD₁与平面ABC₁D₁`的公共点是不难的，因此命题可得证。

实例2 证明：一条直线与三条平行直线相交，那么这四条线共面

这是一个文字叙述的命题，一般需先由题意画出图形，然后写出已知、求证。

已知：a//b，b//c，a∩d=D，c∩d=F

求证：a，b，c，d 共面

下面我将由三步思维模式探讨如何证明这个问题。

（1）寻求证明依据

欲证线共面问题，我们先想想哪些定理涉及到共面问题，有公理3，推论1推论2推论3都涉及共面问题。因此要证明线共面问题就得依据这些命题了，但这些定理所涉及到的线只有两条，而要直接由这些定理说明四线共面，显然是难以做到的，下面我们再进入第二步思维。

（2）由条件得出相关结论，建立条件与结论的关系。

经上述分析后，我们遇到了麻烦，为此我们不妨审视一下条件，条件中涉及到的是平行线与交线，显然由定理我们可得出这样一些结论：

　①

当然,下面只需证明直线也在平面内即可， 但若沿着这一思路向下论证时，我们发现直接证明在内是不很容易的，我们会遇到难以解决的麻烦。条条大道通罗马，我们不妨探索一下其它途径，再回头重新审视一下条件，同样可以得到：

②

由①②不难得出：

为此，刚才还感到郁闷的问题迎刃而解。

实例3 如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。

这是高二数学（下A）教科书P10的定理。下面我主要以三步思维模式谈谈对这个定理的证明思路。

先将文字语言翻译为为数学符号语言，写出已知、求证。

已知：

求证：

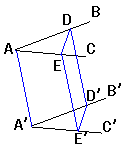
这是空间两个角，存在两种情况，在同一个平面内或不在同一个平面。对于前一种情况证明较简单。下面我着重谈谈当不在同一平面时如何证明。

（1）由结论出发，寻求证明依据

欲证，首先回顾一下哪些定理涉及到角相等问题或者说通过什么来说明两角相等呢？有同位角、内错角、对顶角、圆周角、相似三角形、全等三角形等，那么哪一个可作为本题的证明依据？审视一下命题题设，不在同一个平面内两个角显然不可能是同位角、内错角、对顶角、圆周角。为此，我们应选择三角形或三角形全等解决这一问题，而题中没有三角形怎么办呢？

（2）条件不足，创造条件，达到目的

由以上分析我们可初步设想用三角形来解决这一问题，为此我们必须依据这两个角构造两个三角形，当然构造全等更容易的多，因此我们可在角的两边取线段，连接，从而构造，下面只需证明即可, 上面的问题就此得到解决。

实例4 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC=AB=1,M是PB的中点.

（Ⅰ）证明：面PAD⊥面PCD；

（Ⅱ）求AC与PB所成的角；

（Ⅲ）求面AMC与面BMC所成二面角的大小.

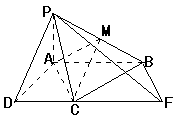
本题是2005年全国Ⅰ高考数学试卷（理科）第18题，我们就此来分析一下本题的解题思路

（1） 要证明面PAD⊥面PCD，由面面垂直判定我们需寻找线面垂直。即一个平面内的一条直线垂直于另一平面即可，那么如何寻找那条垂线呢？我们由面面垂直的性质知道两垂平面内垂直于交线的直线必垂直于另一个平面，就是说我们在一个平面内要寻找另一个垂直平面的垂线，我们只需在这个平面内寻找交线的垂线即可，根据这一思路，我们知道PD = 面PAD∩面PCD，而观察图形发现面PCD内直线CD垂直于交线PD，为此我们找到面PAD的垂线CD，下一步只需证明CD⊥面PAD即可。

（2） 欲求AC与PB所成的角，根据要解决的问题出发，思考哪些定理涉及异面直线所成角的问题，显然教材中并没有这一相关定理，为此求异面直线AC与PB所成角我们只能根据周大福定义将这一空间角的问题化为平面角来解决，我们借助和手段就是寻找异面直线的平行线，使其转化到同一平面内，当然首先观察图形中有无AC与PB的平行线，通过观察，图形中并没有AC与PB的平行线，为此我们需创造条件，作出辅助线，当然作AC与PB的平行线的方法有很多，在这里我仅仅给出一种作法，其它的供读者自己探讨。找到AC所在的平面ABCD与PB的交点B，过B作与AC平行的直线，延长DC于E，连结BE、PE，可证BE//AC，则∠PBE（或其补角）就是异面直线AC与PB所成的角。下面只需在△PBE内解出∠PBE即可。

（3） 欲求面AMC与面BMC所成二面角的大小，根据我们所学知识，有两种解决办法，①利用射影面积公式，②根据二面角定义直接作出二面角。若利用办法①，则需寻找某一个面的垂线。若利用办法②则需寻找二面角棱的垂线。无论哪一种方法，我们都必须解决一个问题，就是寻找垂线。那么题中条件虽然明显给出了一些垂直关系，但还有一些线间关系我们是不知道的，题目中告诉了一系列数据会不会隐藏着其他垂直关系。下面我们计算这几个几何体内各个线段的长度，不难计算；不难发现△AMC≌△BMC，这就是说只需过A作AF⊥MC，连BF，则BF⊥MC，也就是意味着我们可直接作出二面角的平面角。显然我们可用办法②来解决。当然能否采用办法①呢？那就是说我们需找到某一面的垂线即可，分析观察寻找面PBC的垂线，可能容易的多。欲找线面垂直。可先找面面垂直，即寻找面PBC的垂面。则又需在面PBC内寻找其它面的垂线，又由刚才的结论BC⊥AC不难得到BC⊥面PAC，则面PAC⊥面PBC，则只需过A作两垂面的交线PC的垂线，就是面PBC的垂线。下面的问题就可自行解决了。

另外，我需要进一步指出的是，以上几个的问题我们也可以用利用向量这个更普遍，更一般的知识解决它，但在这里我仅仅探讨的是如何思维的问题，对于如何使用向量这一工具需要在读者熟练掌握向量知识以后自己去探索一下，在这里我不再赘述了。

通过以上四个实例的探讨,我们应该可以初步了解用三步思维模式解决立体几何中证明问题的基本思路，其中对于实例1、2、3，列举的是教科书中的最基础的内容，目的是能让初接触立体几何的读者能够迅速上手而不至于感到困惑，而实例4中除了问题(1)是证明问题，(2)(3)两个问题则是计算求值问题,但你会发现也同样可以用三步思维模式来思考解决它，这也正说明了三步思维模式是解决立体几何问题的更一般的方法.它是我们学好立体几何的重要手段，也是提高我们思维能力的重要途径。

附实例4解答：（Ⅰ）证明：因

由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.又DC在面PCD上,故面PAD⊥面PCD.

（Ⅱ）解：因

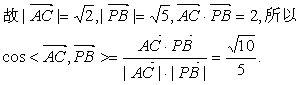
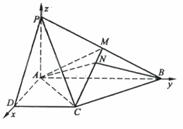
（Ⅲ）解：在MC上取一点N（x,y,z）,则存在 使

         要使

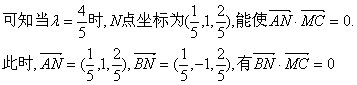
         为所求二面角的平面角.