现代教育强调"知识结构"与"学习过程"，目的在于发展学生的思维能力，而把知识作为思维过程的材料和媒介。只有把掌握知识、技能作为中介来发展学生的思维品质才符合素质教育的基本要求。数学知识可能在将来会遗忘，但思维品质的培养会影响学生的一生，思维品质的培养是数学教育的价值得以真正实现的理想途径。
高中学生一般年龄为15—18岁，处于青年初期。他们的身心急剧发展、变化和成熟，学习的内容更加复杂、深刻，生活更加丰富多采。这种巨大的变化对高中学生的思维发展提出了更高的要求。研究表明，从初中二年级开始，学生的思维由经验型水平向理论型水平转化，到高中一、二年级，逐步趋向成熟。作为高中教学教师，应抓住学生思维发展的飞跃时期，利用成熟期前可塑性大的特点，做好思维品质的培养工作，使学生的思维得到更好的发展。
教育心理学理论认为：思维是人脑对事物本质和事物之间规律性关系概括的间接的反映。思维是认知的核心成分，思维的发展水平决定着整个知识系统的结构和功能。因此，开发高中学生的思维潜能，提高思维品质，具有十分重大的意义。
思维品质主要包括思维的灵活性、广阔性、敏捷供、深刻性、独创性和批判性等几个方面。思维的灵活性是建立在思维广阔性和深刻性的基础上，并为思维敏捷性、独创性和批判性提供保证的良好品质。在人们的工作、生活中，照章办事易，开拓创新难，难就难在缺乏灵活的思维。所以，思维灵活性的培养显得尤为重要。
思维的灵活性指思维活动的灵活程度，指善于根据事物的发展变化，及时地用新的观点看待已经变化了的事物，并提出符合实际的解决问题的新设想、新方案和新方法。学生思维的灵活性主要表现于：(1)思维起点的灵活：能从不同角度、不同层次、不同方法根据新的条件迅速确定思考问题的方向。(2)思维过程的灵活：能灵活运用各种法则、公理、定理、规律、公式等从一种解题途径转向另一种途径。(3)思维迁移的灵活：能举一反三，触类旁通。
如何使更多的学生思维具有灵活特点呢？在教学实践中作了一些探索：
一、以"发散思维"的培养提高思维灵活性
美国心理学家吉尔福特（J·P·Guilford）提出的"发散思维"(divergent thinking)的培养就是思维灵活性的培养。"发散思维"指"从给定义的信息中产生信息，其着重点是从同一的来源中产生各种各样为数众多的输出，很可能会发生转换作用。"
在当前的数学教学中，普遍存在着比较重视集中思维的训练，而相对忽视了发散思维的培养。发散思维是理解教材、灵活运用知识所必须的，也是迎接信息时代、适应未来生活所应具备的能力。
l、引导学生对问题的解法进行发散
在教学过程中，用多种方法，从各个不同角度和不同途径去寻求问题的答案，用一题多解来培养学生思维过程的灵活性。
<例>求证：
证法1：（运用二倍角公式统一角度）
证法2：（逆用半角公式统一角度）
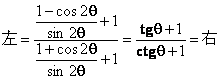
证法3：（运用万能公式统一函数种类）设
证明4：
(构法分母
并促使分子重新组合，在运算形式上得到统一。)
证法5：可用变更论证法。只要证下式即可。
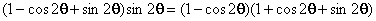
证法6：由正切半角公式
，利用合分比性质，则命题得证。
通过一题多解引导学生归纳证明三角恒等式的基本方法：(1)统一函数种类；(2)统一角度；(3)统一运算。
一题多解可以拓宽思路，增强知识间联系，学会多角度思考解题的方法和灵活的思维方式。
2、引导学生对问题的结论进行发散
对结论的发散是指确定了已知条件后没有现成的结论．让学生自己尽可能多地探究寻找有关结论，并进行求解。
<例>已知：
(1)，
(2)，由此可得到哪些结论？
让学生进行探素，然后相互讨论研究，各抒己见。
想法一：(1)2＋(2)2可得
（两角差的余弦公式）。
想法二：(1)×(2)，再和差化积：
结合想法一可知：
想法三：(1)2-(2)2再和差化积：
结合想法一可知：可得 
想法四；
，再和差化积约去公因式可得：
，进而用万能公式可求：
、
、
。
想法五：由消去
得：
；消去
可得
（消参思想）
想法六：(1)+(2)并逆用两角和的正弦公式：
(1)-(2)并逆用两角差的正弦公式：
想法七：(1)×3-(2)×4：
，
即 
则、、均可求。
开放型题目的引入，可以引导学生从不同角度来思考，不仅仅思考条件本身，而且要思考条件之间的关系。要根据条件运用各种综合变换手段来处理信息、探索结论，有利于思维起点灵活性的培养，也有利于孜孜不倦的钻研精神和创造力的培养。
3、引导学生对问题的条件进行发散
对问题的条件进行发散是指问题的结构确定以后，尽可能变化已知条件，进而从不同角度和用不同知识来解决问题。
对于等差数列的通项公式：an＝a1＋(n－1)d，显然，四个变量中知道三个即可求另一个（解方程）。如"｛an｝为等差数列，a1＝1，d＝－2．问－9为第几项"等等。然后，放手让学生自己编写题目。编题过程中．学生要对公式中变量的取值范围、变量之间的内在关系、公式的适用范围等有全面的掌握。否则，信手拈来会闹出笑话。上题中，若改d＝－3，则－9为第项，显然荒谬。如此，学生对于等差数列的通项公式与求和公式的掌握会比较全面，而且能站在较高层次来看待问题，提高思维迁移的灵活性。
二、以思维灵活性的提高带动思维其他品质的提高，以思维其他品质的培养来促进思维灵活性的培养
由于思维的各种品质是彼此联系、密不可分的，处于有机的统一体中，所以，思维其他品质的培养能有力地促进思维灵活性的提高。
1、思维的深刻性指思维过程的抽象程度，指是否善于从事物的现象中发现本质，是否善于从事物之间的关系和联系中揭示规律。
<例>方程sinx＝lgx的解有（ ）个。
（A）1 （B）2 （C）3 （D）4
学生习惯于通过解方程求解，而此方程无法求解常令学生手足无进。若能运用灵活的思维换一个角度思考：此题的本质为求方程组
的公共解。运用数形结合思想转化为求函数图家交点问题，寻求几何性质与代数方程之间的内在联系。通过知识串联、横向沟通牢牢抓住事物的本质，在思维深刻性的基础上，思维灵活性才有了用武之地。
2、思维的广阔性是指善于抓住问题的各个方面，又不忽视其重要细节的思维品质。要求学生能认真分析题意，调动和选择与之相应的知识，寻找解答关键。
<例>已知抛物线在y轴上的截距为3，对称轴为直线x＝－1，在x轴上截得线段长为4，求抛物线方程。
解法一：截距为3，可选择一般式方程：
显然有c＝3，利用其他条件可列方程组求a，b值。
解法二：由对称轴为直线x＝－1，可选择顶点式方程：
显然有m＝－1，利用其他条件可列方程组求a，k的值。
另外，由图象对称性可知x轴上交点为(l，0)和(－3，0)。
解法三：由截距为3，即过三点(0，3)、(l，0)和(－3，0),
可选择一般式方程：
代人点坐标，列方程组求a，b，c值。
解法四：由一元二次方程与一元二次函数关系可选择两根式：
（必须与x轴有交点）
显然；x1＝－3，x２＝1。由截距3，可求a值。
在把握整体的前提下，侧重某一条件作为解答突破口，在思维广阔性的基础上，充分运用思维灵活性调动相关知识、技能寻找解题途径。
3、思维的敏捷性指思维活动的速度。它的指标有二个：一是速度，二是正确率。具有这一品质的学生能缩短运算环节和推理过程。思维灵活性对于思维速度和准确率的提高起着决定性作用。
<例>相邻边长为a和b的平行四边形，分别绕两边旋转所得几何体体积为Vａ（绕a边）和Vｂ（绕b边），
则Vａ：Vｂ＝（ ）
（A）a：b （B）b：a （C）a2：b2 （D）b2：a2
用直接法求解：以一般平行四边形为例。如图，可求: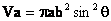
， 
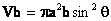
则Vａ：Vｂ＝b：a，由于要引入两边夹角
来求解，学生常无法入手。若以特殊的平行四边形 ──矩形来处理，则相当简便。
此题解法充分体现了思维灵活性，以简驭繁，用特殊化思想求解，解题迅速、正确。
4、思维的独创性指思维活动的独创程度，具有新颖善于应变的特点。思维的灵活性为思维的独创性提供了肥沃的土壤，为解题"灵感"的闪现提供了燃料。
在教学实线中，我常发现，学生提出富有个性的见解的时候,往往是"思维火花"闪烁的时候．
<例>求值： 
一般解法：
独特灵活的解法1：令
，
则
，
即
，则原式
构造对偶式求解，思维灵活颇有独创牲。
解法2：构造1为直径的圆内接三角形，三个角为
，
则
可构成三角形三边长。
逆用余弦定理：
则原式
灵活的构想独特巧妙，数形结合思想得到充分体现。我在教学中比较注重学生解题思路的独特征、新颖性的肯定和提倡，充分给予尝试、探索的机会，以活跃思维、发展个性。
5、思维的批判性指思维活动中独立分析的程度，是否善于严格地估计思维材料和仔细地检查思维过程。我在数学教学中，鼓励学生提出不同的甚至怀疑的意见，注意引导和启发，提倡独立思考能力的培养。
<例>⊿ABC中，
，
，求 
大部分学生如此解：由可得
；由可得
，进而可求
或
。
有学生提出异议：
由
可知：
，同理可知
。
由
知：
不可能！即
取不到。
故只有一解
学生对结论的可靠程度进行怀疑，在独立分析的基础上，灵活运用三角函数的单调性来确定三角形内角的取值范围，严密论证了三角函数值取值的可能性。
三、灵活新颖的教法探求和灵活扎实的学法指导
教师的教法常常影响到学生的学法。灵活多变的教学方法对学生思维灵活性的培养起着潜移默化的作用，而富有新意的学法指导能及时为学生注人灵活思维的活力。
"导入出新"──良好的开端是成功的一半。引人入胜的教学导入可以激发学习兴趣和热情。以"创设情境"，"叙述故事"、"利用矛盾"、"设置悬念"、"引用名句"、"巧用道具"等新颖多变的教学手段，使学生及早进入积极思维状态。
"错解剖析"──提供给学生题解过程，但其中有错误的地方。让学生反串角色，扮演教师批改作业。换一个角度来考察学生的知识掌握情况，寻找错误产生的原因，以求更好的加深对知识的掌握。
"例题变式"──从例题入手，变换条件寻求结论的不同之处；变换结论寻求条件的不同之处；变换提出问题的背景，寻求多题一解；变换问题的思考角度，寻求一题多解；……以变来培养学生灵活的思维。
"编制试卷"──列出考查知识点、考查重点、试题类型，让学生自己编制一份测验试卷．并给出解答。使学生站在老师的角度体验出题心理，更好的掌握知识结构和思维方式。
"撰写小论文"──根据学习体会、解题经验、考试心得等等，撰写学科研究性小论文。选择比较好的指导修改并编辑出版，激励学生善于进行总结，培养良好的思维品质读档。
以上只是我在培养学生思维灵活性方面的一些实践和体会。
几年来，所教学生在经过有目的的培养后，思维品质都有了很大的提高。相应的，学生的学习质量也有了很大提高。许多学生进入大学、甚至走上工作岗位后，常常来信谈及虽然数学知识有许多已经遗忘，但老师教的数学思维方式却常令他们在工作、学习、生活中得益不少。
近年来，随着课程教材改革的推进，突出思维品质的培养已成为广大教师和教育工作者的共识。我要继续探索下去，以求获得更多的收获。
参考文献：
(1)《中学生学习心理学》 编写组著 广东高等教育出版社
(2)《中学生心理学》 林崇德著 北京出版社
(3)《数学教育学》 田万海著 浙江教育出版社
(4)《高中生心理学》 郑和钧/邓京华等著 浙江教育出版社
(5)《中学生素质教育》 徐仲安著 上海科学技术出版社