数列新教材的特点及其教学设计

1 教材更新的几个特点及其意义

1.1 创设问题情境，注重数学过程

在教材内容的引入方面，第三章一开头就以古代印度的关于国际象棋棋盘上放麦粒的传说故事设置悬念：如何计算，启迪学生思考，提高学习新一章内容的积极性。等差数列的前n项和的引入，以德国数学家高斯两两结合简捷算出，让学生发现等差数列的性质：，再引出倒序求和方法。对等差数列、等比数列的概念引入也改变旧教材从一个数列直接引出定义，而是从三个特殊数列通过设问，观察其共同特点，从特殊到一般，让学生体会定义过程。

习题编排也注意了培养学生的归纳思维：新教材上的习题中，第10题关于等差中项、等比中项的性质让学生从特殊到一般，推出，。尽管用通项公式可以方便证明，但用八个问号编排使学生学会从特殊归纳一般的数学发现方法。

新教材注意了扩充整合知识，拓展思维空间。充要条件概念在旧教材数列部分没沾边，而新教材有多处呈现。在等差中项概念正逆叙述后还特意设问是、A、b成等差数列的充要条件吗？等比中项概念也正逆叙述。另外在参考例题中特意将旧教材中一个例题：RtΔ三边长成等差的性质证明改用充要条件命题，双向证明。在复习参考题中也有充要条件命题出现。众所周知，充要条件是数学思维的基本模式，也是序的本质诠释。新教材对此予以强化，正是通过数学概念间逻辑联系的方向性，让学生体验和理解概念形成的过程。

1.2 利用教材特点,渗透数学思想

由于数列可以看作是一个定义域为正整数集（或它的有限子集｛1，2，…n｝）的函数当自变量从小到大取值时对应的一列函数值，所以继函数之后提前编排数列教学，承上启下，顺理成章，恰到好处．同时数列内容所反映的基本数学思想和方法比较丰富，运用的初中知识也较多，如数式的运算、变换，基本量观点、方程思想和待定系数法等。

新教材P116页的例2：在等差数列｛｝中已知求首项和公差d。p121的例4已知一个等差数列的前10项的和是310，前20项的和是1220，由此可以确定求其前n项和的公式吗？等例题都是新增编的基本例题，让学生掌握常用的数学思想方法，如方程思想、基本量思想、待定系数法等。特别是p117上的例4：已知数列的通项公式为，其中p、q是常数，且p≠0，那么这个数列是否一定是等差数列？如果是，其首项与公差是什么？这个例题是新教材编写的“代表作”，一方面直接揭示了等差数列的判定方法之一，同时从其图象表示可以看出等差数列的几何意义；另外还可以从一次函数的两个基本量看出等差数列由和d=p所确定。可谓是一举三得。

新教材利用数列教材内容的特点，尽力展示函数与方程、等价转化、数形结合、分类讨论等数学思想方法，为学生体验数学过程，感悟数学文化提供了众多素材。

1．3 丰富教学内容，拓展思维空间

新教材的另一个显著特点是丰富了教学内容，增加辩证思维容量，努力促进学生智力成长，培养数学理性思维。主要表现：一 ，明确定义了数列的递推公式概念。教材以等差数列前后项的关系，实例引入，给出递推公式定义，让学生理解递推公式也是给出数列的一种方法，培养学生由此及彼的联想思维能力；其二，教材与时俱进，更新内容，增加了子数列、和数列、以及数列的线性运算等内容，一方面加深对等差、等比两类基本数列有关性质的理解，另一面将数列内容中的辩证唯物主义观点，如对立统一、运动变化、普遍联系、互相转化的思想方法充分展示出来，拓展了教与学的思维空间，有利于学生的智力成长和理性思维的培养。

如p118和p128练习中第3题都是特殊数列（等差、等比）对去掉前k项、取出所有奇数项、以及每隔一常数（如7、10）项取出一项的子数列的研究。又如p119由｛｝、｛｝为等差数列（项数相同），探讨｛｝（其中p、q是常数）的等差性质；p127由｛｝、｛｝为等比数列（项数相同），研究｛·｝的等比性质；以及p129｛｝（＞0）为等比数列，求证｛｝是等比数列。再如p123研究群数列=1+2+3+……+（n-1）+ n+（n-1）+……+3+2+1以及p123、p133研究等差、等比数列的分段和数列，的等差、等比性质等等。

新教材为我们奉献了理想的重要课程资源。如何利用和开发好新课程资源，实现课程改革宗旨，如何以人的发展为本，转变教学理念，倡导和实施建构的学习，把教育重心移到培养学生的数学素质和创新能力上来，是摆在我们教育工作者面前必须认真思考的问题。下面就数列内容的总体教学设计谈一些浅见。

2　多元的有效教学意图和教学对话策略

数列内容的新课程设计与时俱进，注重了数学过程，渗透数学思想和拓展思维空间。基于对课程与教学一体化的认识，我们的教学设计需要与新课程相对应的新的教学观。教学的目的在于帮助每一个学生进行有效的学习，教师须精心策划多元的有效教学意图，实施教学对话、体验过程的交流互动策略，使学习者得到尽可能充分的发展。

2.1 丰富课程思考以拓展学生视野

对数列内容应该从以下四方面丰富思考，帮助学生理解知识，拓展视野，即“背景、程序、辩证、回归”。

1）函数是源，数列是流。背景,即揭示背景，对数列知识理解更深刻。数列有关概念、性质只是函数相应概念、性质在限制自变量n∈N^*下的体现。如等差数列的通项、求和公式分别是n的一次、二次函数（缺常数项）；等比数列的通项、求和公式分别是指数函数的一次复合：、（q≠1）；尤其是分段函数思想在数列学习中学生时常疏忽。如，。

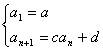2）定义是源，结构是流。程序,即理解程序性知识，迁移、运用知识更自然。中学里学习的数列知识主要是等差、等比两类特殊数列以及它们的组合、变式。对等差数列，其通项公式的归纳求法、求和公式的倒序相加、等差性质、判定等差,…,都是由等差定义推出；对等比数列其通项归纳、求和公式的错项相减、等比性质、判定等比，…，也都由得到。对于等差、等比数列的子数列、分段和数列以及它们的组合、变式均可以用特殊数列定义转化。如递推数列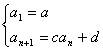其中C≠0、C≠1、，其特例即等差数列、等比数列。

3）关系是源，形式是流。辩证,即以辩证观点认识数列，虽然数列给出方法千变万化，形式各异，但其数学关系，基本量的结构关系是源头。一方面认识问题，运用辩证观点以揭示其关系为基本策略，抓住关系就是牵住了牛鼻子；另一方面变换问题，围绕关系辩证选择变换策略，或者利用已知关系，变换问题形式。

4）生活是源，数学是流。回归，即生产、生活、实践是数学学科知识的直接源泉。数学思维是对客观实际的抽象、概括、总结。等差、等比数列知识是现实中等量增、减，指数变化的模式概括。其实四则运算中的加减、乘除（指数运算不过是连续乘而已…）及其混合的规律性变化在现实生活中随处可见。山林木材的等比年增长，银行存款的复利计息、城市建设住房总面积的等比增长，…如果伴随着年末等量砍伐利用、等额取用款子、旧房的等量拆除，…即所谓等比、差复合问题。引导学生体验一类问题共性，归纳领悟其数学模式，使教学既源于具体情境，又超越具体情境，学生获取的才是高于真情实感的，能动而有活力的知识。

2．2　体验数学过程的教学对话策略

下面从一题多解（例1）、多题一解（例2、例3、例4、）的两个教学案例，认识让学生经历数学活动、体验数学过程的教学对话策略的具体运用。

例1：已知数列｛｝的项满足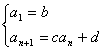（其中C≠0， c≠1）证明这个数列的通项公式为。

与学生一起分析，递推式中当 c=1时｛｝为等差数列；当d=0, c≠0，时，｛｝为等比数列。

该数列的递推公式中，前后项的关系是一次线性，不妨称为等比差数列。推导其通项公式，方法较多，体现了数列问题的基本变换和技巧，可以与学生一起探讨。

证一阶差法，由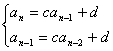两式相减，消d, 便有,即｛｝成等比数列，求后再迭加。

证二：待定系数法。设，比较系数，，使得｛｝成等比数列，下略。

证三：逐乘消项法。

由，逐次乘以（t=n,n-1,…2）迭加消项，要运用等比求和等知识。

证四：数学归纳法（略）

证五：不完全归纳法。由题设

,……

一般化有，化简即是。

不完全归纳法虽然不够严谨，但对培养学生的归纳思维，猜想能力很有帮助,教学中应予重视。

由于在生产实践、社会生活中等比、等差的混合变化的实际问题比较普遍，因而例1作为此类问题的数学模型相对显得重要。下面举几例让数学回归生活的典型例题供读者体验、运用;同时，可以借此培养多题一解的数学理性思维。

例2：分期付款中的有关计算。

设购买一件售价为元的商品，采用分期付款方式，要求在m个月内将款全部付清，分n次付款（n是m的约数）月利率为p，求每次付款数。

（本例系教科书p133研究性课题）

解一：要求m个月内付清，分n次付，每次间隔m/n个月。设每次均还x元。

第一次还款后尚欠；

第二次还款后尚欠［］；

第三次还款后尚欠；……

第n次还款后清，即∴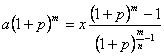

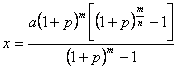
解二：商品增值与还款连息两个量分别考虑：商品增值，

还款连息：列成等式，即有x.

解三：用例2递推公式解：设第t次还款后尚欠，

则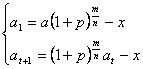

由例1,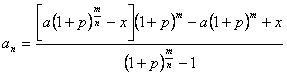, 令，每次还款x值同解一答案。

三种解法比较，解二较简洁（不妨叫做：分线单独分析法）。解一用归纳思想，解二体现降维思维，解三说明例2是例1的实际应用。

例3：某地现有居民住房的总面积为㎡，其中需要拆除的旧住房面积占了一半。当地有关部门决定在每年拆除一定数量的旧住房的情况下，仍以10％的住房增长率建设新住房。

（1）如果10年后，该地的住房总面积正好比目前翻一番，那么每年应拆除的旧住房总面积x是多少？

（2）过十年还未拆除的旧住房总面积占当时住房总面积的百分比是多少？（教科书末应用题）

解（1）：用分线单独分析。

10年中住房总面积增长为，

10年所拆旧房,即

（2）

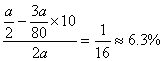
例4:某山林现有木材储量约1000立方米，预计每年增长木材约10％而每年冬季须砍用50立方米枯老木材，设n年后山林木材可以翻番，求n的范围。

解：设n年后木材总量可翻番，分线考虑：

长材：，

砍材（若不砍也长）：，

由题意 - 　化简为 　

一题多解，多题一解是数学思维的中行外汇牌价基本素质，只有在学习过程中，有意识地将知识迁移、组合、融合,激发好奇心，体验多样性，学懂学透，数学能力,创新思维才能与日俱增。

新课程改革提倡“用教科书教”，这给教师带来了极大的自主创造空间。新课程为倡导建构学习，培养理性思维作了示范，而我们教师是课程资源的有机组成部分。只要遵循学生的认知规律，让学生自主学习,经历数学活动（练习、实践）,体验数学过程（反思、理性化），就能拓展课程资源，以活泼、清新、富于理性思维的内容参与教学，拓展空间，激活思维，提高素质，以实现新课程改革的初衷。