提要 函数图象的变换是中学数学的重点内容，因其抽象性，学生理解起来有相当的困难，所以，它也是学习中的难点内容．传统教学中的纸笔画图方式难以有效地解决这个难点问题．如果在教学中能充分利用信息技术形象直观、便于探索研究的优势，就可以有效地发挥学生的学习主体性，通过他们的动手操作、实验和探索，让他们较好地理解和掌握这部分内容，从而提高课堂教学和学习的效率．
主题词 函数图象 图象变换 信息技术
函数图象的变换是函数教学中的重点内容，也是难点内容．但因为函数的抽象性，学生对此理解起来比较困难，即使学生能记住教师归纳出来的规律并能简单应用，但他们还是对此感到模糊不清．传统的纸笔画图方式因其静态的缺陷，难以对学生的理解和掌握起到真正的帮助，而信息技术能使数学“视觉化”的形象直观的特点和便于探索研究的优势正好弥补了传统方式的缺陷．笔者在教学《函数》一章时，利用专题讲座的形式，借助《几何画板》，引导学生对此进行了有益的尝试和探索，收到了较好的效果．以下就是笔者的教学案例及其分析．
一、平移变换
笔者课前先用《几何画板》画出指数函数
及
、
的图象，设置动画按扭（课前制作好课件，主要是想避免因学生对技术使用不熟练而影响上课的时间）．上课时，由学生自己操作，动态演示当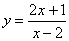
、
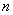的值发生变化时，函数和的图象的变化情况，并与函数的图象进行对照比较，初步得出图象平移的变化规律．然后再由师生共同考察相关图象上的对应点P、Q的坐标及变化情况，具体分析平移的距离（图1），从而归纳概括出图象平移的规律．
图1
平移规律：（1）f (x) → f (x+m) ： m>0时，向左平移m个单位；m<0时，向右平移∣m∣个单位．
（2）f(x) → f(x)+n ： n>0时，向上平移n个单位；n<0时，向下平移∣n∣个单位．
思考：对于二次函数y=ax2+bx+c(a≠0)，参数a、b、c的取值变化对函数的图象有什么影响？
学生回顾以前所学过的有关知识并回答后，教师利用课件直观形象地演示函数图象随参数a、b、c的变化而变化的情况（图2），既复习了有关知识，又巩固了平移变换的知识．
（学生观察图1后能很快发现平移方向与 、 的取值的关系．但对点P、Q的坐标变化情况还是费了一点周折，主要是学生难于找到平移后点P、Q的对应点．在教师的指导下，绝大部分学生都能完成操作并发现规律．从后面的练习1、2的完成情况来看，学生基本上都能正确解答这两题，这说明学生掌握得是比较好的．这与不用技术时反复强调和练习后仍有部分学生模糊不清形成鲜明的对比．）
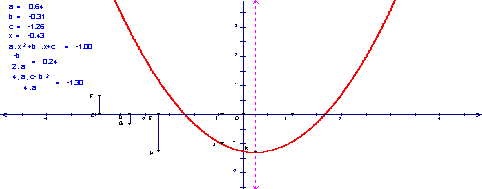
图2
二、对称变换
（1）利用《几何画板》的函数作图功能，让学生随意选择一个函数y=f(x)作出其图象，并依次作出函数y =-f(x)、y =f (-x)、y =-f (-x) （图3）、y =︱f (x)︱、y =f (︱x︱) （图4）的图象，再对照函数y=f (x)的图象观察分析．然后改变函数，同样处理，从而归纳概括出相应的对称变换规律．
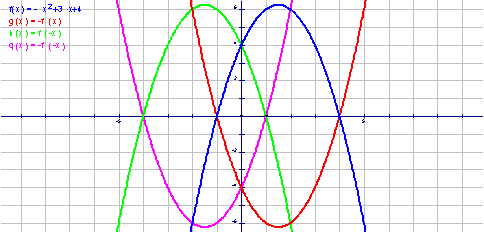
图3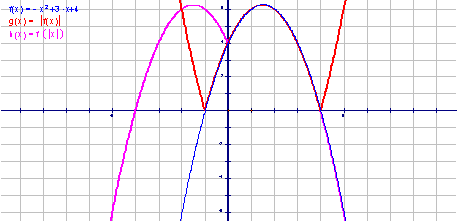
图4
变换规律：① y = -f (x)的图象与y = f (x)的图象关于x轴对称；
② y = f (-x)的图象与y = f (x)的图象关于y轴对称；
③ y = -f (-x)的图象与y = f (x)的图象关于原点对称；（回顾初中学过的点的对称 情况，此结论不难理解和解释）
④ y =︱f (x)︱的图象：保留y = f (x)的图象在x轴上及其上方的部分，并将x轴 下方的部分关于x轴对称到x轴上方（代数分析：因为︱f (x)︱非负，故函数图象总位于x轴上及其上方）；
⑤ y =f (︱x︱) 的图象: 保留y = f (x)的图象在y轴右边的部分，并将y轴右边的部分关于y轴对称到y轴左边（代数分析：因为函数y =f(︱x︱)是偶函数，其图象关于y轴对称）．
（学生能很快地画出函数图象，并观察出变换规律，但对图4中两个图象的变换规律的归纳叙述还不够清楚和准确．经过学生的讨论和交流，在教师的引导下，最终归纳概括出上面的规律，然后对其作出代数分析．这说明，技术的使用可以帮助学生理解和掌握相关知识内容，但是，相关的数学表达等方面的能力的训练，还有待于在日常的教学活动中逐渐进行．）
（2）让学生随意画出几个指数函数的图象，观察它们在第一象限内的图象特征，得出规律：当底数 越大时，函数图象就越靠近y轴（即图象右端在上方）；当底数
越小时，函数图象就越靠近x轴（即图象右端在下方）．（图5，相应颜色的图象对应于相应颜色的函数，图6与此相同）
然后，画出相应的对数函数的图象（图6中的虚线图象）．在指数函数的图象上各任取一点，作出它们关于直线y=x的对称点，则对称点在相应的对数函数的图象上．追踪对称点的轨迹可知，它即是相应的对数函数的图象．通过这个操作过程，复习了指数函数与对数函数互为反函数以及互为反函数的函数图象关于直线y=x对称的相关知识．
（学生对于画图和观察发现规律感到问题不大，但因学习基础的原因，他们对图6中对称点的轨迹与相应的对数函数图象之间的关系在理解上还是感到有些困难．教师先让他们回顾函数图象的描点作图法，再引导他们明确函数图象即是满足某种条件的点的集合，从运动变化的观点来看，就是满足某种条件的点运动以后留下的痕迹—轨迹．这样一来，学生就感到释然了．）
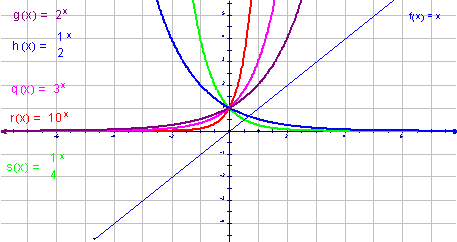
图5
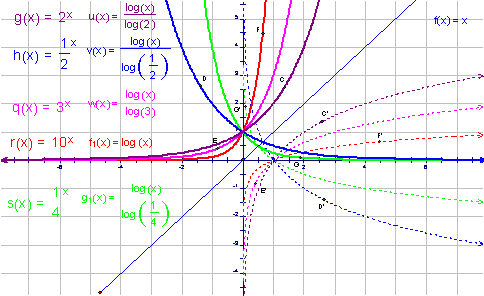
图6
三、练习
(1) 画出函数
的草图．
(2) 求出函数的图象的对称中心及函数的单调区间．
（关键是引导学生将函数式进行“分子常数化”的变形：
，从而找到与它有关系反比例函数
．对此，学生感到困难．引导学生变形后，通过讨论，大部分学生均能顺利地分两步解答此题．）
(3) 如何由y = lgx的图象通过变换而得到y=-lg∣x∣+2的图象？
（此题有些复杂，教师应适时引导：由y = lgx的表达式通过怎样的变形可得到y = -lg∣x∣+2的表达式？每一步变形代表着什么图象变换？如此，大部分学生就能分三步解答此题：先变绝对值符号，再变负号，最后上平移．部分学生还提出了另一种变形方法：先变负号，再变绝对值符号，最后上平移．其实，这是学生第一次接触函数图象的平移和对称变换，没有必要、也不可能要求每一个学生都能立即掌握复杂的变换问题．只要他们能较好地理解和掌握本节课的相关知识和规律就行．在今后的教学中，还需要对此进行相应的训练，以巩固所学．）
通过以上的教学过程，不但使学生直观形象地理解和比较牢固地掌握了函数图象变换的相关知识和规律，更为重要的是，这使学生在学习方式的转变方面进行了有益的尝试，学生也积累了学习的体验和经验，他们从被动地接受知识转变为主动地参与教学、参与操作、发现知识、掌握知识，成为了学习的主人，发展了实践能力和创新精神．当然，经验的积累、学习方式的转变、能力的培养，远不是几节课就能完成的，这需要教师在平时的教学活动中有目的地进行安排和实施．本节课的实践，为今后的教学提供了有益的例子．