教学何谓有效?是教师精彩的上课,还是学生考试的高分数?现代观点强调:衡量教学的有效与否,是学生的进步与发展,是学生学习的长期性、可持续性,是教与学有机结合的体现。具体来说,我们的教学应关注学生良好学习品质、良好思维品质的培养,关注学生学习能力的提高,关注学生的情感、态度、科学价值观等个性品质的获得。
怎样实现和提高教学的有效性,是我们探讨的方向,也是新课程提出的目标。教材是实现课程目标,实施有效教学的重要资源,所以我们在教学中对新课程的教材要做到“三个把握”,从而实现“三个有效”,最终达到提高教学的质量。
(一)把握教材的空白空间,有效培养学生良好的学习品质
学习品质包括学习的兴趣、学习的方式、方法、学习的习惯,怎样有效培养学生良好的学习品质?在传统的教学中,一些教师(尤其是一些经验丰富的教师)为学生想得很周到,讲得清楚、详细,却使学生养成了过于依赖老师的习惯,处在被动接受的状态,这种把数学学习当成是记忆一些重要的数学结论,而忽视对学生的发展和可持续学习能力的培养的教学已不适应时代的发展。美国教育家布鲁纳曾说过“学习不是被动机械地形成刺激—反应的联结,而是主动形成认知结构的过程”。事实上,激发学生学习的兴趣,、改进学生的学习方式和学习方法,使学生学会学习,为终身学习和发展打下良好的基础正是高中数学课程的基本理念。新课程教材在编写设计上与旧教材有一个明显不同,新教材为引导学生自主发现、探索留有比较充分的空间。在教学中我们应充分利用这些空白空间,再给予学生发挥的时空,,促进他们主动地学习和发展。如:在人教版的《数学必修4》探讨三角函数的单调性,教材首先引导学生利用正弦函数在一个周期的图像探讨单调区间,并归纳推广出一般结论:对于余弦函数单调区间的探讨,教材没有画出图像,也没有写出结论,这就要求学生运用研究正弦函数性质的方法来研究余弦函数,探究后得出一般性结论,再进行填空。这是教材第一次出现这种填空,老师不能替代,只能引导学生逐步进行,也许学生没有什么收获;也许因此而完成不了当时的教学任务,但从效果看:由老师讲、学生学的短期效果较好;而由学生自己探究的却具有长期效应,兼顾长短期目标我们既要重视基础教学,又要从发展学生智力着想,采取循序渐进,鼓励引导学生不断改进学习方式,大胆进行思考、探究。教材也正是沿着这一方向进行,思考、探究、填充等逐渐增多,如由![]() 的公式怎样得到
的公式怎样得到![]() 公式,结论是什么?由
公式,结论是什么?由![]() 、
、![]() 公式又怎样得到
公式又怎样得到![]() ,结论又是什么?我们的教材都在不断引导学生探究、推导、归纳,留下许多问号和空白让学生完成。又如学习完《数列》一章后,教材设计了全章知识结构框图的填充,让学生自己回顾小结。这些设计都给人耳目一新,对培养学生良好的学习品质有积极作用,复习的效果也事半功倍。让空白的地方丰富多彩也是学习方式丰富的表现,,许多学生能利用书本大片空白作归纳总结,记录自己的研究发现、学习心得;翻开学生的书本就能猜出学生学习的成效:学困生的书本崭新崭新的,空白的仍然是空白;而优等生的书本里面写满了东西,有的记录每单元的重点、难点;有的记录着错例的剖析或学习体会评注等等。有一个学生在学完了函数
,结论又是什么?我们的教材都在不断引导学生探究、推导、归纳,留下许多问号和空白让学生完成。又如学习完《数列》一章后,教材设计了全章知识结构框图的填充,让学生自己回顾小结。这些设计都给人耳目一新,对培养学生良好的学习品质有积极作用,复习的效果也事半功倍。让空白的地方丰富多彩也是学习方式丰富的表现,,许多学生能利用书本大片空白作归纳总结,记录自己的研究发现、学习心得;翻开学生的书本就能猜出学生学习的成效:学困生的书本崭新崭新的,空白的仍然是空白;而优等生的书本里面写满了东西,有的记录每单元的重点、难点;有的记录着错例的剖析或学习体会评注等等。有一个学生在学完了函数![]() 的图像与性质后,在旁边空白处写道:只要把
的图像与性质后,在旁边空白处写道:只要把![]() 看作一个整体,再结合基本函数
看作一个整体,再结合基本函数![]() 的性质就能解决求最值、单调区间、对称等问题;有一个学生在《数学必修5》的
的性质就能解决求最值、单调区间、对称等问题;有一个学生在《数学必修5》的![]() 的B组4题下面的空白处记录着:
的B组4题下面的空白处记录着:![]() 可以推广到
可以推广到![]() ;到现在为止求数列前n项和的方法已有三种:(1)倒序相加法:(2)公式法:(3)裂项相消法。充分把握课本的素材与空间,让学生探索求真,主动参与教学的全过程,有助于
;到现在为止求数列前n项和的方法已有三种:(1)倒序相加法:(2)公式法:(3)裂项相消法。充分把握课本的素材与空间,让学生探索求真,主动参与教学的全过程,有助于
(二)把握教材例、习题的潜在功能,有效培养学生良好的思维品质
(1)利用例、习题的典型性、示范性,训练学生思维的有序性和表述的条理性
思维和语言有密切关系。一个语言表达水平低的人绝不可能具有高度发展的思维,尤其是数学语言,要经常在文字语言、图形语言、符号语言中转换,而又侧重于用图形、符号语言来书写表达。在教学中发现,相当的学生对数学问题无从下手、不会分析思考,在推理过程中前后不连贯,思路混乱,也有的知道怎样做,但不会表达或表达不规范,处在有水倒不出的尴尬局面,严重影响水平的发挥。课本的例题尽管简单,但蕴含着重要的数学思维方法和思想精髓,具有典型性和示范性,有助于我们牢固掌握书本的基础知识和基本技能,进而提高综合能力。例如:《三角恒等变换》有角度变换、函数名称变换和式子结构间的变换,容易使学生摸不着头脑,必须经过系统的引导、训练。《数学必修4》P139例题:已知Sinα=![]()
![]() ,
,![]() ,Cos
,Cos![]() -
-![]() ,β是第三象限角,求Cos(α-β)的值。
,β是第三象限角,求Cos(α-β)的值。
要引导学生分析:要求Cos(α-β)的值,联系C(α-β)公式和本题的已知条件,需要作哪些准备?让学生逐步理清思路。解答从哪里开始书写有利,在书写过程要注意什么?由Sinα求Cosα时,开方取什么符号?总之,在学习例题时,让学生明确怎样分析、怎样联想,为什么要这样写。通过例题的学习,使学生领会分析思考的条理性和书写表达的规范性,练就扎实的基本功,从而达到举一反三、变式引申。
如:P150习题3.1
4:已知 α ,β都是锐角,Cosα = ![]() , Cos(α+β) =
, Cos(α+β) = ![]() , 求Cosβ的值。
, 求Cosβ的值。
5:已知Sin(300 +α) = ![]() , 600
, 600 ![]() α
α![]() 1500 求Cosα的值。
1500 求Cosα的值。
只要进行恰当的角度变换,这两个问题实质上与例题一样,因为β=(α+β) –α,α = (300+α) -300 ,也就是已知两角的正、余弦值,求这两角的差的余弦值;但如果不善于作分析,或受定势思维的负迁移,有的学生把Cos(α+β)展开来求Cosβ,其结果都难以成功。学习等差、等比数列时,学生对证明等差或等比数列的问题上不会表述,大部分都只会列举。究其原因:教材只引导学生归纳了定义的文字表达形式,教学上很有必要补充式子符号表达,即:若数列![]() 满足
满足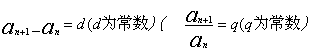 ),则数列
),则数列![]() 为等差(等比)数列。然后才能较好地完成如
为等差(等比)数列。然后才能较好地完成如![]() 的例3和
的例3和![]() 的例4。认识数学知识的本质特征,理清思维程序并恰当表述是良好思维品质的基本要求。
的例4。认识数学知识的本质特征,理清思维程序并恰当表述是良好思维品质的基本要求。
(2)利用例、习题的联系性,有效训练学生思维的深刻性和批判性
数学知识由纷繁复杂的客观世界抽象而来,思维的深刻性和批判性也是学习数学知识的必要条件。很多教师都有一个发现:在学习单个知识时,学生似乎学得不错,但学完了多个知识或一个系统后,却变成简单的题目都不会,这除了综合能力不高外,还与平时不作归类整理、没有把各个局部知识按照一定的观点和方法组织成整体有关。二倍角公式的理解就不能只知道2α是α的二倍角,类似的:4α是2α的二倍,α是![]() 的二倍,如P146 例5:已知Sin
的二倍,如P146 例5:已知Sin![]() =
=![]() ,
, ![]() , 求4
, 求4![]() 的三角函数值。
的三角函数值。
分析:由![]()
![]() ,两次运用二倍角公式;又如P152 例1:
,两次运用二倍角公式;又如P152 例1:![]() Cosα=2Cos 2
Cosα=2Cos 2 ![]() - 1 = 1 – 2Sin2
- 1 = 1 – 2Sin2 ![]()
![]()
![]() Cos 2
Cos 2 ![]() =
=![]() , Sin2
, Sin2 ![]() =
= ![]()
![]() tan2
tan2 ![]() =
= ![]()
这实际上是二倍角公式的逆向运用,得到的半角公式(或降幂公式)。有了对例题的深刻理解就能解决一类问题,如求![]() 的值;化简
的值;化简![]() 等。
等。
通过变式、逆用、一题多解等训练思维的深度,引导学生不满足表面知识,能深入钻研问题,探求各种知识的联系,从而找到解决问题的本质和规律。在新课程的教材中的确十分注意挖掘数学知识的内在联系,如《数学5》学习等差数列时把通项公式与一次函数联系,前n项和公式与二次函数联系,等比数列的通项与指数函数联系;学习一元二次不等式与二次函数和一元二次方程联系,注意相关内容的前后联系,使学生加深对所学知识的系统认识,促进思维的深刻性。
不迷信书本和老师,敢于主动、独立、批判的探讨问题也是当代创新人才的思维品质。在教学上要鼓励学生敢于提问、敢于发表自己的不同观点,《数学4必修》习题3.1第8题,在 △ABC中![]() ,
,![]() ,求CosC值。我在批改作业时,没有考究教材参考资料提供的答案(
,求CosC值。我在批改作业时,没有考究教材参考资料提供的答案(![]() 实际上只有
实际上只有![]() ),结果把正误答案颠倒。发现错误后,我主动向全班同学道歉,并表扬了敢于坚持真理的同学。及时提出新问题:(1)在 △ABC中若
),结果把正误答案颠倒。发现错误后,我主动向全班同学道歉,并表扬了敢于坚持真理的同学。及时提出新问题:(1)在 △ABC中若![]() ,
,![]() ,求CosC值。有几个解?(2)在 △ABC中,
,求CosC值。有几个解?(2)在 △ABC中,![]() 成立吗?留给学生课外思考、讨论。学习了正弦定理后,再回头证明。通过这一问题的深刻探讨,不但使学生牢固掌握知识,更大大提升了学习的自信心和学习的热情,在潜移默化中培养了学生的科学态度和理性精神。在学习《数学必修5》的等比数列前n项和知识时,训练
成立吗?留给学生课外思考、讨论。学习了正弦定理后,再回头证明。通过这一问题的深刻探讨,不但使学生牢固掌握知识,更大大提升了学习的自信心和学习的热情,在潜移默化中培养了学生的科学态度和理性精神。在学习《数学必修5》的等比数列前n项和知识时,训练![]() 第2题:在等比数列中:已知
第2题:在等比数列中:已知![]() 在求解过程中学生得到了:
在求解过程中学生得到了:![]() ,进一步发现:
,进一步发现:![]() 成等比数列 ,这就对应于完成第70页的习题B组第2题,继续引导这一结论推广,完成第76页的复习参考题A组第10题,证明:等比数列的
成等比数列 ,这就对应于完成第70页的习题B组第2题,继续引导这一结论推广,完成第76页的复习参考题A组第10题,证明:等比数列的![]() 也成等比数列。学生们总结前面的经验也较顺利地完成了证明,心理充满了成功的喜悦。真的没有漏洞吗?鼓励学生探讨其严谨性,有学生举出了反例:数列 1,-1,1,-1……是公比q= -1等比数列,但
也成等比数列。学生们总结前面的经验也较顺利地完成了证明,心理充满了成功的喜悦。真的没有漏洞吗?鼓励学生探讨其严谨性,有学生举出了反例:数列 1,-1,1,-1……是公比q= -1等比数列,但![]() ,并不是等比数列;这一发现令人吃惊,因为在课本和其他所有的课外书都没有此说法。从理论上讨论:当
,并不是等比数列;这一发现令人吃惊,因为在课本和其他所有的课外书都没有此说法。从理论上讨论:当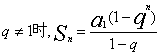 显然当n为偶数且q= -1时,
显然当n为偶数且q= -1时,![]() ,
,![]() 不可能为等比数列。不人云亦云,敢于用批判的观点去探索是科学的基本态度,在教学过程中,应当充分把握课程资源肩负培养学生理性精神和批判性思维习惯的使命。
不可能为等比数列。不人云亦云,敢于用批判的观点去探索是科学的基本态度,在教学过程中,应当充分把握课程资源肩负培养学生理性精神和批判性思维习惯的使命。
(三)把握教材的辅助材料,有效培养学生的个性品质
培养良好的个性品质和数学素养在新课标中明确提出, 学生要具有一定的数学视野,认识数学的科学价值和人文价值,崇尚数学的理性精神,形成审慎思维习惯。 新课程的教材更加重视数学的文化价值观的渗透,在许多地方安排了“阅读与思考”、“探究与发现”等辅助材料,如果我们在进行教学的同时采取多种形式利用好这些辅助材料,就能极大地开阔学生视野、训练数学技能,更深刻地挖掘数学的文化内涵,从而有效培养学生的个性品质。如“探究与发现”的《互为反函数的两个函数图象之间的关系》、《解三角形进一步讨论》等内容可结合课堂教学内容,采取穿插渗透式,作为课堂的拓展与引申,进一步促进学生对所学知识的理解,完善认知结构;而“阅读与思考材料” 《函数概念的发展历程》、《三角与天文学》、《对数的发明》等则可以在课外活动中,以讲座形式,由教师或学生讲述,让学生了解数学发展中的重大发现,激发学生不懈追求的志向;同时关注数学的应用意识,引导学生用数学眼光从生活中捕捉数学问题,并主动地运用数学知识解决问题,如“探究与发现”《购房中的数学》就是有趣且实用的素材,可以采取分组形式,组长负责制,发动学生到售楼中心,银行调查、搜集购房的相关信息,分别就商业贷款、公积金贷款、一次性购房等不同支付方式,写出报告,并以小论文形式论述购房的最佳方案,并进行论文评奖,组织答辩,充分调动学生参与的积极性,让学生充分感受数学的实用性,品尝成功的喜悦。总之,在知识教育的同时,让学生通过数学文化的学习,可以了解人类社会发展与数学发展的相互作用,认识数学发生、发展的必然规律;了解人类从数学的角度认识客观世界的过程,体会和认识数学的文化价值,促进学生科学观形成,全面提高学生的数学素养。
在新课程改革的大潮中,我们应更新观念,更多地关注学生的发展与未来。把握新课程教材的“度”,合理灵活使用教材,发挥教材各种潜能,改进教学方法,引导学生改进学习方式,在主动学习中参与教学的探究、思考过程,变“学会”为“会学”,努力提高教学的有效性,从而提高教学质量。
参与资料:《数学课程标准解读》江苏教育出版社
《现代教育学》广东高等教育出版社
《心理学》广东高等教育出版社