初中阶段已经讲述了函数的定义,进入高中后在学习集合的基础上又学习了映射,接着重新学习函数概念,主要是用映射观点来阐明函数,这时就可以用学生已经有一定了解的函数,特别是二次函数为例来加以更深认识函数的概念。二次函数是从一个集合A(定义域)到集合B上的映射?:A→B,使得集合B中的唯一元素y=a![]() +bx+c(a≠0)与集合A的元素X对应,记为?(x)= a
+bx+c(a≠0)与集合A的元素X对应,记为?(x)= a![]() +bx+c(a≠0)这里a
+bx+c(a≠0)这里a![]() +bx+c表示对应法则,又表示定义域中的元素X在集合B中的象,从而使学生对函数的概念有一个较明确的认识,
+bx+c表示对应法则,又表示定义域中的元素X在集合B中的象,从而使学生对函数的概念有一个较明确的认识,
事实上,函数的概念来自于生活实践,来自于社会中各个量之间错综复杂的相互关系。 反过来我们又可以根据函数来探索、确定现实生活中各个变量之间的关系,从而解决实际问题。
第一部分 教学案例
资料1:65%个税来源于工薪阶层 个税改革牵动工薪一族
来自国家税务总局的消息说,2004年中国个人所得税收入为1737.05亿元,其中65%来源于工薪阶层。“贫富倒挂”的现状激起了各方的反应,一时间“个税改革”的问题成为街头巷尾热论的话题。
目前,除北京、上海执行1200元,深圳执行1600元起征的个人所得税标准外,全国其他地区执行的仍旧是800元的“老标准”。这个始于1980年的个税起征点,在经历了25年的经济发展和物价上涨后,显然已经不能适应新的形势了。
1980年月收入800元的算高收入阶层,但25年后的今天,“月薪800元”已经成了低收入的代名词。用20多年前的标准当作现在的起征点,显然已经脱离实际。因此,这让人们对此次个税改革充满了期待。
标准提高压力减小
记者从北京市地税局个税管理处了解到,从2003年9月1日开始,北京市每人每月的补贴免税扣税额,由200元提高到400元,个税工薪项目起征点,也由1000元提高到1200元。以北京某国企职工李先生为例,他的月收入为2000元,按照1200元个人所得税起征额,他每月应缴纳个人所得税金额为55元,一年为660元。如果按照 800元的个人所得税起征额,他每月应该缴纳的个人所得税金额为95元,一年为1140元,二者相差近一半。
这对于收入本来就不高的李先生来说,“显然提高了起征标准之后,压力就小了一半。”
个人所得税知多少
个人所得税是对个人(自然人)取得的各项所得征收的一种所得税。其征收范围包括:工资薪金所得;个体工商户的生产、经营所得;对企事业单位的承包经营、承租经营所得;劳务报酬所得;稿酬所得;特许权使用费所得;利息、股息、红利所得;财产租赁所得;财产转让所得;偶然所得;经国务院财政部门确定征税的其他所得。
——摘自新浪网
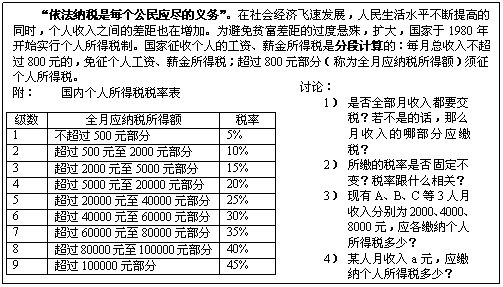
资料2:“依法纳税是每个公民应尽的义务”。在社会经济飞速发展,人民生活水平不断提高的同时,中国个人收入差距存在着不断扩大的趋势。为避免贫富差距的过度悬殊,缓解分配不公,促进社会公平,国家于1980年开始实行个人所得税制。国家征收个人的工资、薪金所得税是分段计算的:每月总收入不超过800元的,免征个人工资、薪金所得税;超过800元部分(称为全月应纳税所得额)须征个人所得税。
附: 国内个人所得税税率表
|
级数 |
全月应纳税所得额 |
税率 |
|
1 |
不超过500元部分 |
5% |
|
2 |
超过500元至2000元部分 |
10% |
|
3 |
超过2000元至5000元部分 |
15% |
|
4 |
超过5000元至20000元部分 |
20% |
|
5 |
超过20000元至40000元部分 |
25% |
|
6 |
超过40000元至60000元部分 |
30% |
|
7 |
超过60000元至80000元部分 |
35% |
|
8 |
超过80000元至100000元部分 |
40% |
|
9 |
超过100000元部分 |
45% |
(本表所称全月应纳税所得额是指依照《个人所得税法》第六条的规定,以每月收入额减除费用800元后的余额或者减除附加减除费用3200元后的余额)
通过阅读材料,思考以下几个问题:
1) 是否全部月收入都要交税?若不是的话,那么月收入的哪部分应缴税?
2) 所缴的税率是否固定不变?税率跟什么相关?
3)现有A、B、C等3人月收入分别为2000、4000、8000元,应缴纳个人所得税多少?
4)某人月收入a元,应缴纳个人所得税多少?请用a表示。
第二部分 教学实案
一、教学课题:§3.12.1 函数的实际应用 课时:第1课时(共2课时)
二、教学目标
(一)知识目标
1.了解数学建模的目的和意义
2.掌握数学建模的一般步骤,会根据已知条件建立函数关系式
(二)能力目标
3.加强现实性,培养学生分析问题、解决问题的能力
4.加强锻炼数学建模能力,培养学生应用数学的意识
(三)情感目标
5.通过让学生感受数学的形成、发展与应用过程,培养学生对数学的兴趣
6.通过案例分析,渗透德育教育,树立依法纳税意识
三、教学重点、难点
重点是根据已知条件建立函数关系式;难点是数学建模意识
四、教学方法
读议讲练法
五、教具准备
多媒体投影仪、电脑设备
六、教学过程
(一)情景设计
【投影一】
|

师:前面,我们已经学习了函数的概念、函数的性质以及一元二次函数的图像和性质,那么它们到底有什么用呢?许多人都以为我又不当数学家,我又不去考大学,只要学会加减乘除就行了,何必去学这么难的函数呢?此话差矣。正如理论来自于实践,又反作用于实践,数学在当今社会各个领域均有着广泛的应用,著名数学家华罗庚说过“数学无处不在,凡是出现"量"的地方就少不了数学”。正因为数学具有广泛的应用性,因此又被称为基础工具学科。接下来我们就通过几个例子来体会数学是如何作用在实践中的。
(二)讲授新课
【投影二】

师:大家首先阅读资料1、2(课前先行下发),来了解一下我国的个人所得税有关知识,并思考下列问题(每4人为一小组,可前后左右讨论,):
5)是否全部月收入都要交税?若不是的话,那么月收入的哪部分应缴税?
6)所缴的税率是否固定不变?税率跟什么相关?
7)现有A、B、C等3人月收入分别为2000、4000、8000元,应各缴纳个人所得税多少?
8) 某人月收入a元,应缴纳个人所得税多少?
(学生阅读材料,小声讨论,教师巡视、启发)
生1:根据资料1,只有收入中超过800元的部分须交纳个人所得税,而不是全部收入。
师:这位同学看资料很仔细,理解也很准确,很好。从中可以发现只有收入超过了800元才需要缴纳个人所得税。这部分称为全月应纳税所得额。下面请另一位同学回答第2个问题。
生2:所缴的税率是变化的。它随着全月应纳税所得额的增加而增加。
师:能不能举例说明,比如个人收入为1000、1500元,应缴的税率各为多少?
生2:个人收入1000元,则全月应纳税所得额为1000-800=200元,税率为5%,应缴个人所得税200×5%=10元;个人收入1500元,则全月应纳税所得额为1500-800=700元,税率为10%,应缴个人所得税700×10%=70元。
师:这位同学分析过程很详细,逻辑很清晰,很好。下面同学有不同意见吗?请尽兴发表,答错也不要紧。
(沉默……。有个别学生小声议论。在教师鼓励下,又一位学生举手发言)
生3:我认为,个人收入1500元时,应缴个人所得税不是70元,而是45元。
(下面学生议论纷纷。教师不加评论,而是把学生的思路引向深入)
师:你是怎么得出这个结果的?
生3:个人收入1500元,则全月应纳税所得额为1500-800=700元,其中500元对应税率为5%,200元对应税率为10%,应缴个人所得税500×5%+200×10%=45元。
师(饶有兴趣地):你是怎样想到把700元分为500元+200元的?
生3:我也说不清,只是感到应该这样:不超过500元部分,税率5%;超过500元到2000元部分,税率10%,而700元中超过500元部分的只有200元,因此对应税率10% 。
师:很好。大家有不同意见吗?
生2:我认为超过500元至2000元部分,应该指700元,而不必分为500元+200元。
师:大家认为怎样?
(下面学生议论纷纷,有说生2对的,有说生3对的。此时学生以达“心有所感,欲说不能”的不愤不悱阶段)
师:好,刚才大家的意见都集中在是否要对全月应纳税所得额按税率进行分段计算。在解决这个问题之前先请大家回答一个问题:如果甲的收入大于乙的收入,那么在交税后甲的收入是否可能小于乙的收入?
生:不可能。
师:对,不可能!个人所得税的目的是抑制贫富差距的过分拉大,而不是贫富一个样;否则就不利于激发大家的积极性,挣钱越多,越不合算嘛。那么接下来请座位左边的同学按照生2的思路、右边的同学按照生3的思路分别算一下:若甲月收入为1301元,乙为1300元,他们分别应缴个人所得税多少?然后互相比较,交税后实际所得谁多谁少?
(教师巡视,请两位同学上来板演)
生4(按照生2不分段思路):
甲月收入1301元,全月应纳税所得额为1301-800=501元,对应税率10%,
故应缴税501×10%=50.1元,得甲税后实际收入1301-50.1=1249.9元;
乙月收入1300元,全月应纳税所得额为1300-800=500元,对应税率5%,
故应缴税500×5%=25元,从而得乙税后实际收入1300-25=1275元;
所以,缴税后乙的收入大于甲的收入。
生5(按照生3分段思路):
甲月收入1301元,全月应纳税所得额为1301-800=501元,其中500元对应税率5%,1元对应税率10%,故应缴税500×5%+1×10%=25.1元,从而得甲税后实际收入1301-25.1=12759元;
乙月收入1300元,全月应纳税所得额为1300-800=500元,对应税率5%,故应缴税500×5%=25元,从而得乙税后实际收入1300-25=1275元;
所以,缴税后甲的收入仍大于乙的收入。
师:由上述同学的解答可以看出:按照不分段的思路求解,就有可能造成税前收入高的一方在税后反而变成了收入低的一方现象;而按照分段的思路求解,税前收入高的一方在税后仍然是收入高的一方,只不过两者间的差距缩小了:由税前相差1元,变成了税后相差1275.9-1275=0.9元。这正是个人所得税的作用,调配社会分配不均,缩小个人收入差距。那么好,我们应选择哪一种思路计算个人所得税?
生(异口同声):按税率对应纳税所得额进行分段计算。
师:好,这正是税率表里各级纳税所得额中“部分”的正确反映!也就是说,在应纳税所得额中应分为不超过500、500-2000、2000-5000、…、100000以上等九部分,这正是解决本道题的关键!下面请大家解决问题3。
(学生互相讨论,计算,教师巡视、个别指导)
【投影三】
|

师:由上面可以看到,首先应确定纳税所得额,并分析等级。然后再依次计算以上各级税额,但在分段计算时应去掉已经计算过的部分。但是上面的计算过程稍嫌麻烦,有没有更一般的方法或公式呢?
【投影四】
 |

根据这个关系式,我们根据收入可以马上得出任何一人的应缴税额,而不必再详细分类,这正是数学的好处。
像上述过程把实际问题转化为数学问题的过程我们称为数学建模。数学建模是解实际问题及数学应用题常用的方法。其基本思维流程如下:


【投影五】
师:下面我们来研究其他几个例题。
【投影六】(多媒体逐步演示)
|

师:面积由哪几部分组成?
生:上面的半圆和下面的矩形。
师:那么它们的面积分别是多少?
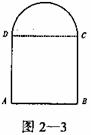
生6:因为半径为x,所以半圆面积为![]() 。……矩形面积求不出。
。……矩形面积求不出。
师:为什么求不出呢?矩形面积不是等于长×宽=AB×AD吗?
生6:AB=CD=2x,但是AD没有告诉我们呀!
师:考虑很仔细,很好!那么AD是否由铁丝弯成的?
生6:是。
师:那么,铁丝总共弯成了哪些边框?它们的总长你知道吗?
![]() 生6:圆弧CD和线段DA、AB、BC、CD,它们的总长是…m! (有学生提示)
生6:圆弧CD和线段DA、AB、BC、CD,它们的总长是…m! (有学生提示)
师:好极了!也就是说:![]() (板书),那么AD能求了吗?
(板书),那么AD能求了吗?
生6:我知道了!
师:好!请你继续回答。
生6:因为AD=BC,AB=CD=2x,而圆弧CD=πx,所以πx +2AD+4x=m,即AD![]()
师:下面请大家继续解决y与x的关系。
(教师巡视,学生练习。投影六显示解答过程)
师:通过此题大家应明确应用的能力要求及求解应用题的基本步骤。(以下板书)
1、 数学应用题的能力要求:
(1)阅读理解能力;
(2)抽象概括能力
(3)数学语言的运用能力;
(4)分析、解决数学问题的能力
2、解答应用题的基本步骤:
(1)合理、恰当假设;
(2)抽象概括数量关系(已知,未知),并能用数学语言表示;
(3)分析、解决数学问题;
(4)数学问题的解向实际问题的还原。
师:接下来请看例2。
【投影七】(多媒体逐步演示)


|

评述:例2是实际应用问题,解题过程是从问题出发,引进数学符号,建立函数关系式,再研究函数关系式的定义域,并结合问题的实际意义做出回答,这个过程实际上就是建立数学模型的一种最简单的情形。
(三)课时小结
师:通过本节学习,大家应对数学建模有所了解。其解题过程主要是从问题出发,引进数学符号,建立函数关系式,再结合问题的实际意义研究函数关系式的定义域,分析函数式做出回答。其关键是正确建立函数关系式。下节课主要针对数学建模做练习,加强锻炼数学的实际应用能力。
(板书):实际问题 引入符号 建立函数关系式* 定义域 解答问题
(四)课后作业
【投影八】
|

八、教学后记
新课标要求我们从人的发展上对课堂教学活动做较大的改革,即“改革教学过程中过分注重接受、记忆、模仿学习的倾向,倡导学生主动参与,交流、合作、探究等多种学习活动,改进学习方式,使学生成为学习的主人”。本文通过案例的引进,创设现实情景使学生乐于参与讨论,在教学过程中对学生的观点注重通过交流、讨论决定取舍,而不是以教师的身份加以评判,从而培养学生的数学科学思维能力,增强学生的数学应用意识;同时渗透德育教育,通过论述所得税的意义,增强学生依法纳税的意识。在案例分析时把重点放在了对“部分”的不同理解上(即问题2),结合案例的实际意义,辨明了是非。笔者以为正确理解问题正是数学建模成败的关键。
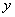 即
即 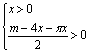 解之得
解之得