[摘要]职高入学没有门槛后,职业教育迎来了新的机遇与新的挑战,同时也冲击着传统的教学观与学生观。既然没有教不好的学生,那么这些学生数学成绩差,不学数学,肯定是教育的责任。基于职高数学课堂有效性的研讨,如何让学生轻松乐意的学,于是提出寻找有效的”问题源”该是首要任务。通过对有效“问题源”几大关注点的探讨,揭示职高数学课堂有效“问题源”的几大切入口。
[关键词]职高数学 课堂教学 问题
1.问题的提出
1.1 问题背景
2002、2003、2005年国务院先后召开全国职业教育工作会议,会议指出努力扩大职业教育规模,大力发展农村劳动力技能培训,提高农村劳动力整体素质,所以职校入学变成没有门槛的了,由此职校学生学习素质之差是可想而知的。2006年秋季对我校553名职高新生进行了数学学习情感特点的问卷调查,结果有73.2%的学生表现为讨厌数学,有13.6%的同学甚至表现为愤怒。面对如此的学生,即使再怎么样的降低教学目标,也是枉然。以至于职高数学课堂启而不发,自启自发现象成了一种普遍的课堂现象。“没有教不好的学生”给教师带来更多的压力与震撼。扪心自问“既然没有教不好的学生,那么这些学生数学成绩差,不学数学,肯定是我的责任”。寻思:“创设怎样的课堂才能让学生轻松,乐意的参与数学课堂学习”?“建构主义的认知是以情意为动力,由学习者主动建构的,是情意与认知的融合”。寻找有效的问题资源使学生对数学学习产生兴趣是首要任务。
2.有效问题
有效问题是那些能够让学生积极组织回答,并因此而积极参与学习过程的问题。问题应该设计成学习者的认知挑战,以引发学习者的兴趣,促进他们获取知识、发展有效的问题解决和高级思维技能。[1]要提问很容易,问何?缘何而问?提出好的问题却很困难。寻找有效的问题资源一般应关注以下几点:
2.1 “有趣”与“有用”的统一
“兴趣是最好的老师”,借助有趣的问题源提问能引起学生的参与热情和学习动机。但“缘何而问”必须先行,当学生感兴趣的抬起头,应不失时机的抓住问题与课程内容的内在联系,切入学生临近发展区的认知区域引起冲突,创设“愤与悱”之境,触发学的冲动,继而激发学生主动参与解决问题。如在学习排列数公式时,问题源可选择一副扑克牌,一可借助它推导排列数公式,二可借助它提问“4个0计算24点”来学习阶乘与0!,一门两用。也可利用“阳光伙伴”体育游戏,学习数列的概念,并在学的潜移默化中增强团队精神。
2.2“师问”与“生问”的和谐
由谁问?问谁?由谁解决问题?从而生成了一个灵动的课堂。有效提问在教学中占有十分重要的位置,要求教师针对教学内容、教学对象和教学环境,深入了解职校学生学习内在障碍的因素,了解学生在学习上的要求和愿望,去寻找问题源。传统的课堂总是学生求解由教师所给出的问题,而很少要求学生主动地去提出问题,这种单一的问题源形式阻碍了学生创新能力发展,所以著名科学家爱因斯坦曾指出:“提出一个问题比解决一个问题更为重要。”所以课前教师应积极开发资源,使预设的问题源应有利于学生生成有效问题源。由下面的课堂教学片断可见一斑:
个 案
余老师的在上排列组合单元的复习课时,她简要的对本节课作了总结后,“同学们,再过几个月,你们就要毕业了。在校学习期间,各任课老师与你们的友好相处,共同进步,你们将拿什么留作永久的纪念呢?”
学生甲:“照张集体相。”其他同学众声附和“对”。
师:“好!我赞成。老师提个小小要求:5位科任老师想跟咱班的五位课代表照张相,你们利用所学排列组合知识,设计一些条件,然后求出各自条件下的所有的不同情况的种数。”
接着余老师出示问题如下:
本班____个任课老师与各自的课代表排成一排照相,根据下列不同的条件,求各有多少种不同的排法?
①____________________________
②____________________________
③____________________________
④____________________________
⑤____________________________
⑥____________________________
⑦____________________________
余老师说明:横线处你们先自己填条件,然后让学生互答。
学生们的想象力非常丰富!提出如下问题:
1、一排照相,英语课代表与体育老师必须站在中间(因为她们俩最高)。
2、排成一排照相,林老师与余老师必须站在中间(因为林老师是我们的校长而余老师是我们的班主任)。
3、师生各自站在一起。
4、5位学生必须排在一起
5、老师不能站在两头
6、5位学生必须相邻
7、每位教师和自己的课代表必须相邻
8、5位学生不相邻
9、师生相间
一石激起千层浪,学生的思维非常活跃,自己提问自己解决,或带着问题走向同学与老师。这种教师投放问题源,学生产生问题链的师生、生生互动,让学生真正成为学习的主人,创造性能力得到了充分的展现。
2.3“个性”与“共性”的兼顾
笔者曾在去年的冬天有幸听了一节〈平面向量的基本定理〉公开课,当时上课老师创设了一个“你们喜欢游泳吗”问题情境。觉得有点不妥,因为大冷天的,大部分学生又没冬泳爱好,所以不能激起学生对问题的愉悦感,结果此问题情境的效应可想而知。课堂是一个动态的情境,应遵循大部分学生共性的经验、、兴趣、态度等,所以教师应寻找让大部分学生产生共鸣的问题源,选择问题源呈现的合适时机,然后兼顾个性的特质、能力与爱好,并充分预设可能达到的目的。如在学习排列组合应用时正好遇上校新生杯篮球赛,由此找到了一个能激发学生学习兴趣的问题源,提出问题“请设计一个由16个班级参与的小组单循环赛”,此时不懂篮球赛比赛规则的同学不知所以然,结果让喜欢打篮球的小王(平时数学课常睡觉)设计并说明,然后共同解决场次问题。做到了个性的关注与共性的发展。
综上所述教师能否找到恰当的“问题源”,设计出有效的问题事关课堂的教学效果。一般不仅取决于数学本身知识的考虑,而且也与学生自身的认知水平、先前经验、家庭背景、能力、个人特质、兴趣、态度等有关,因此这样的“问题源”一般不能直接在课本内找到,而只能依据教师针对教学内容、教学对象和教学环境来具体构建,创造性地去设计。职业高中数学课堂应该选择怎样的“问题源”呢?
3.寻找有效“问题源”的几大切入口
3.1从生活入口
有教育价值的课堂活动,应该是指能够满足学生经验的连续、互动的活动。所以其问题源应选择学生熟悉的生活场景,着眼于他们日常经验和现有经验。从学生的日常生活中发现、挖掘、选择性的提炼“问题源”,促成有效的课堂活动,实现自我发展。如在数列应用学习中可出示如下问题:
某同学利用暑假时间到一家商场勤工俭学。该商场向他提供了三种付酬方案:第一种,每天支付38元;第二种,第一天付4元,第二天付8元,第三天付12元,依此类推;第三种,第一天付0.4元,以后每天比前一天翻一番(即增加1倍)。你会选择哪种方式领取报酬呢?
职业中学强调工学研读,每年暑假都有社会岗位实践活动,所以算工资的生活场景耳濡目染。也是他们急待解决的问题,由此能持续保持学生的学习兴趣。
3.2从发展入口
杜威的课程理论中明确指出课程的目标是保护与促成发展。有个性的生长与社会性的生长。个性的生长包括学生身体发育、心理与情感的成长、思维与理智能力的发展;而社会性它不仅包涵着对社会进步所需要的知识、文化遗产的继承、传播和创造。所以应引导学生主动积极的参与课堂活动,考虑学生兴趣、本能和习惯等特质,面对经验与活动进行择取和排序,另外应重视学生的一定的文化环境、民族环境和社群环境的成长,最后还应循序渐进,不可拔苗助长。如在〈空间图形性质的应用〉教学中本人是这样设计的:先课件展示2003年8月9日温州晚报新闻:文物考古部门人士呼吁,尽快修复江心东塔,该主题问题情境。在世界历史百塔之一的修复背景中,学生形成自主参与、乐于探究等学习习惯,形成搜集、获取、处理信息的能力以及提出分析解决问题的能力,通过以东塔的修复方案为主线的付之人文气息的实际问题的解决,形成对美的追求,激发爱乡情绪,以及积极向上不畏艰难的精神,这种有效的利用本乡本土的资源,遵循时代性与地域性。充分关注个体的发展,调动了人性的冲动与激情。
3.3从经验入口
经验是学习的起点,所以如何从学生的个体经验中挖掘有教育意义的“问题源”,重视学生所学经验与原有经验的联系,引导学生原有经验的扩大或更深理解。所以教师应在学生“邻近(边缘)发展区寻找“问题源”进行内发性与建构性的学习。如在学习〈向量内积的运算〉时,可源于学生已有的实数运算法则:交换律、结合律与分配律,结合最近发展区向量的概念、线性运算与内积的概念学习的基础上,采取类比的思想假设联想向量是否也有相应的运算法则。通过知识的迁移、同化与顺应。把知识内化为自身头脑中的知识网络结构。
3.4从专业入口
职业教育是就业为主的教育,职业高中的文化科应遵循够用与适用,应与专业科进行有机的整合,突出文化科的服务功能,所以教学中问题源也应突出专业特色。下面为本人担任汽修专业班数学教学,在学习一次函数的应用时,问题源的选择,权作抛砖引玉:
个 案
从专业入手寻找问题源:源于暑假汽修专业老师小杨因学校委派,到某公司实践培训时,某一天所发生的事情:
1、开车至某超市购物
问题1、一种矿泉水,单价为1.5元,试写出这种矿泉水瓶数x和总价值y之间的函数关系。
巩固练习:(从生活经验找到问题的生长点)
1)一种矿泉水,零售价为1.5元/瓶(12瓶以下),批发价为1.1元/瓶(12瓶以上包括12瓶),试写出这种矿泉水瓶数x和总价值y之间的函数关系。
2)一种食物,如果单价不变,购买4公斤需付64元,写出这种食品重量x和总价值y之间的函数关系。归结:确定一个函数的步骤
(1) 写出解析式,其中未知系数用字母表示
(2) 把已知数据代入函数解析式,解方程(或方程组)
(3) 解方程(或方程组),解出"待定系数"
(4) 把求出的"待定系数"值回代原来的函数解析式,得到所求的函数
(5)数学问题的解向实际还原.
(从生活入手创设生活场景,超市出来后,发现自己的驾座漏机油,于是生成新的问题源。)
2、汽车出故障
问题2、汽车储油3升的油箱,如果每分钟流出![]() 升,求油箱所剩余的油量Q升和流出时间t(min)的函数关系式。
升,求油箱所剩余的油量Q升和流出时间t(min)的函数关系式。
(从发展入手找到问题源)请问上面的汽车能否安全的以60Km/h的速度开到20Km外的汽车维修点?
(从专业入手排查故障。)
3、故障排查轴向柱式油泵出问题
汽车的轴向柱式油泵出故障(运用flash动画演示它的工作状态,寻找有效的问题源)
问题3、弹簧匯率原长为2.5cm,在0.5N到40N 的力作用限度内,每增加1N时,弹簧就伸长0.05cm,求弹簧长度l与力F的函数关系。
(围绕问题的发现和解决,从发展入手挖掘问题源)
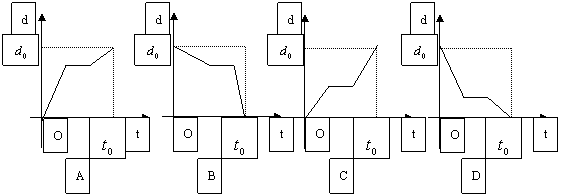
问题4、.小杨与同事事先约好某时刻在学校旁的汽车维修点集中,一起参与实习作业.由于时间还早,他从家里出来后一开始便开的很慢,途经某超市时,看看时间还早,便在超市里面购买了矿泉水与食物,出来后,发现汽车出故障,以较快的速度在规定时间赶到汽车维修点,如果用纵轴表示离汽车维修点的距离,横轴表示出发后的时间,则下列四个图形中比较符合小李走法的是( )

总之,数学是思维的体操,职业高中数学的课堂是灵动的,而问题是思维的接生婆,没有问题的思维是肤浅的思维。如何让职高学生积极参与课堂,做一个问题发现与解决的积极者与主动者,首先就是教师应引导学生课前去挖掘资源,要让学生形成有时刻寻找问题源的意识。只有在不断的解决问题,产生新问题,再解决问题,再产生新的问题-----的过程中思维受到熏陶与激励,在多思与深思中培养良好的思维品质。
[参考文献]
1.钟启泉等主编 . 为了中华民族的复兴 为了每位学生的发展 . 华东师范大学出版社 . 2001,8
2.(美)坎贝尔等. 多元智能教与学的策略.王成全译.北京:中国轻工业出版社,2001.3.
3.顾泠沅主编.数学教育 从理论到实践.上海教育出版社
4.戴再平主编.开放题 数学教学的新模式.上海教育出版社
[1] Chuska,1995;Wilen,1991