建构主义下的中小学数学作业处理方法探讨

关键词：建构主义，协作学习，支架式教学模式，新型的数学作业处理方法。

在我国传统教育“刺激—接受”的模式下，中小学的大部分数学作业是学生被动完成的。因为教师要求做，学生才完成。而教师的批改，因为时间紧，大部分作业也只是简单机械地打“√”与打“×”。于是作业“多、空、假”的现象普遍存在。这种现象直接影响着学生的学习兴趣，也严重地影响教学质量的提高。学生本应该用在学习他们感兴趣、有意义的事情上的时间，被许多重复作业无情地夺走；教师把本应该放在教学研究与备课上的时间,全花在了学生作业的机械批改上。这是一种低效的劳动，毫无疑问应该改进。但目前很难看到成功的改进办法，究其原因是传统的教育思想的影响根深蒂固地束缚着教师与教育管理者的思想，教师更没有理由自己去改变这种现状。要想从根本上改变这种现象，必须从教育思想上提高认识。

一 传统教育思想与建构主义教育思想的比较

我国的教育思想历来倾向以教师为中心，“为人师表”，“师道尊严”，“传道、授业、解惑”，这既是我们祖先留传下来的良好师德，也是以教师为中心的传统教育思想的真实写照。这种教育思想的优点是有利于教师主导作用的发挥，有利于教师监控整个教学活动进程，有利于系统科学知识的传授，有利于教学目标的完成。这种教育思想，对于知识、技能的学习掌握，对于全面打好学生的各学科知识基础是有利的。

不足之处是由于长期“重教轻学”，忽视学生的自主学习、自主探究，容易造成学生对教师、对书本、对权威的迷信，并且缺乏发散思维、批判思维和想象力，这样培养出来的大多是知识应用型人才，而非创新型人才。这正是我国当前教育的致命弱点。我国素质教育的指导方针是：“要实施以培养学生的创新精神与实践能力为重点的素质教育”。如果完全沿用传统的教育思想我们就不可能培养出21世纪所需要的具有创造精神与合作精神的人才。

但是，来自西方的建构主义认为，知识不是通过教师传授得到，而是学习者在一定的情境下，借助学习获取知识过程中的其他人（包括教师和学习伙伴）的帮助，利用必要的学习资料，通过意义建构的方式而获得。

“建构”同时是建立和构造关于新知识认识结构的过程。“建立”是指从无到有的兴建；“构造”是指对已有的材料、结构、框架加以调整、整合或者重组。学习者对新知识的学习，同时包括建立和构造两个方面，既要建立对新知识的理解，将新知识与已有的适当旧知识建立联系，又要将新知识与原有的认知结构相互结合，通过纳入、重组和改造，构成新的认知结构。一方面新知识由于成为结构中的一部分，就与结构中的其它部分形成有机联系，从而使新知识的意义在心理上获得了建构；另一方面原有的认知结构由于新知识的进入，而更加分化和综合贯通，从而获得了新的意义，可见建构新知识的过程，既建构了新知识的意义，又使原认知结构得到了重建。

学生与环境的相互作用涉及两个基本过程：“同化”与“顺应”。同化是指把外部环境中的有关信息吸收进来并结合到学生已有的认知结构中，即个体把外界刺激所提供的信息整合到自己原有认知结构内的过程；顺应是指外部环境发生变化，而原有认知结构无法同化新环境提供的信息时所引起的学生认知结构发生重组与改造的过程，即个体的认知结构因外部刺激的影响而发生改变的过程。同化是认知结构数量的扩充，而顺应则是认知结构性质的改变。学生就是通过同化与顺应这两种形式来达到与周围环境的平衡：当学生能用现有知识去同化新信息时，他是处于一种平衡的认知状态；而当现有知识不能同化新信息时，平衡即被破坏，而修改或创造新知识的过程就是寻找新的平衡的过程。学生的认知结构就是通过同化与顺应过程逐步建构起来，并在“平衡──不平衡──新的平衡”的循环中得到不断的丰富、提高和发展。这就是建构主义的基本观点。

从建构主义的教育思想来看，它更强调对学生的自主性、创造性与合作精神的培养，正好弥补了我国传统教育的欠缺。由此可见，我国的传统教育思想与西方建构主义的教育思想是一种互补的思想结构，我们应该在继承传统教育的同时，努力地改进我们教育的缺陷，才能达到素质教育的目的。

二 新型作业处理方法的探讨与实践

如果我们抛弃传统的作业评判方式，从布置作业开始，就应用建构主义的支架式教育模式来设计学生的作业及批改，那么我们的工作将会是怎样的情况呢？

支架式教学模式的五个主要环节是：

⑴ 搭脚手架──围绕当前学习主题，按“最邻近发展区”的要求建立概念框架。

⑵ 进入情境──将学生引入一定的问题情境(概念框架中的某个节点)。

⑶ 独立探索──让学生独立探索。

⑷ 协作学习──进行小组协商、讨论。

⑸ 效果评价──对学习效果的评价包括学生个人的自我评价和学习小组对个人的学习评价，评价内容包括：①自主学习能力；②对小组协作学习所作出的贡献；③是否完成对所学知识的意义建构。

笔者的做法如下：

第一步 教师在新知识教学之后，认真分析各类学生现有的数学基础，以及他们的最邻近发展区的数学知识，设计一套题量适当、由浅入深、由易到难的习题，它们分别是基础题、巩固题、综合发展题三种题型，并分类标号，如：A1、 B3、 C1，为学生搭脚手架。

第二步 教师宣布作业不要求上交，学生围绕教师设计的题与问题尽自己能力想与做，教师只做抽样调查，但对独立做完题的或比上次多做题的同学施行奖励，以此创设问题情景。

第三步 学生从易到难独立作业。教师明确表示题目可以不做完，但必须完成以下任务：

1. 写出本次作业中，你独立完成的题的标号，按做题的顺序编排。目的在于搞清学生新旧知识的构建情况，将不同的学生分类，为下一步的教学做准备。

2. 在所做的题中你用到了哪些知识？这些知识你正确掌握了吗？目的在于梳理知识，考查学生自主学习的能力，为再学习做准备。

3. 写出本次作业中途卡壳的题的题号。思考卡在哪里？与什么知识有关？目的在于引导学生如何建立知识的联系，找到问题所在。

4. 写出不动笔的题的题号，你认为不会做的原因在哪里？目的在于找到学习难点，为寻找帮助者做准备。

第四步 协作学习，要求同学相互交流，但严禁抄袭。按下列步骤进行：

1. 公布自己会做题的题号，寻找同号伙伴，相互交流各自的做法，学习别人的不同方法，推出团体的最优方法并将此方法告知老师。

2. 公布自己卡壳题的题号，寻找会做此题的团体，加入其中，寻找卡壳的问题症结所在，讨论解决问题。

3. 公布自己不会做的题号，寻找此题开始卡壳并且现在会做的同学伙伴，加入其中，相互帮助，相互学习讨论油價解决问题。

4. 全体不会做的题，在教师的分层启发下，教师与同学一起探讨完成。

这种充分的信息交流与沟通，相互的学习与帮助，使学生们会做的题数，象滚雪球一样不断增大，知识在相互协作的学习中不断的同化与顺应，最后形成意义的建构。

第五步 效果评价 教师应在第三、四步进行的过程中，认真分析学生做题的题号及顺序，从中发现学生的问题与知识的欠缺，及时指出，也为后期教学做准备。帮助学生寻找相应的伙伴，并对积极参与活动的同学给予鼓励，让有好而新的解题方法的同学充分表现自己。对不同类型学生的作业进行抽样调查，适时分类指导。对学习确实有困难的同学要认真辅导，耐心帮助，及时鼓励。

教学实例片段精选：

课题：图形变换的应用

1 提出问题，创设情境。（造桥选址问题，选自人教版七年级下册），如图1，A和B两地在一条河的两岸，现要在河上造一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直.）看谁能最迅速地架一座最好的桥？

2 分层设题，辅助建架。

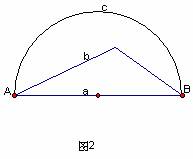
A1题：如图2，A、B是平面上不重合的两点，在连接A、B的所有连线中，最短的一条是：

A、 线段a ； B、 折线b ； C、 曲线c； D、以上都不对.

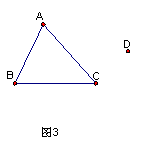
A2题：如图3，已知△ABC及点D，求作△DEF，使△DEF由△ABC平移得来，且点D是点A的对应点。在作图过程中，想一想哪些线段相等？为什么？

A3题：如图4，画出点A关于直线l的对称点A1. 点B是直线上的另一点，线段AB与A1B相等吗？为什么？

B1题：如图6，要在公路m旁建一所小学，使A村、B村到小学的距离之和最小，请作出小学的位置。

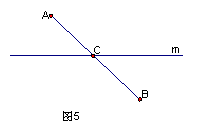
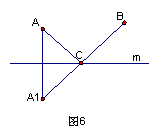
分析讨论：如图5，若A、B两村分布在公路m两侧，则只需连结A、B，AB与公路m的交点C即为所求. 这时，AC+BC =AB. 依据连结A、B两点的连线中，线段AB最短. 但是此问题中A、B两村分布在公路m的同侧. 因而利用对称变换作出A点关于公路m的对称点 A1，就可转化为前面的情形来解决了.

作法：如图6，①作A点关于公路m的对称点A1. ②连结A1B与公路m交于C.

③连结AC、BC，则C就为学校的位置.

B2题：如图7，在给定的锐角∠AOB内有一点M，试分别在OA与OB上求点P与Q使△MPQ的周长最小.

分析讨论：要使△MPQ的周长最小.须使MP+PQ+QM成一条线段. 如图8，假设△MPQ为所求三角形，延长QP至M1，使PM1=PM，延长PQ至M2使QM2=QM. 则△MPQ的周长为线段M1M2（最短）. 所以此问题关键在于确定M1和M2.即利用对称变换作出M点关于OA和OB的对称点M1和M2就能解决问题.

作法：如图8，①作出M点关于OA的对称点M1，

作出M点关于OB的对称点M2.

②连结M1M2与OA交于P与OB于Q.

③连结MP、MQ.

则△MPQ为所求作三角形.

B3题：已知点A、B是直线m的异侧且到m的距离不相等.

求作：在直线m上求一点，使与点A、B的距离之差为最大.

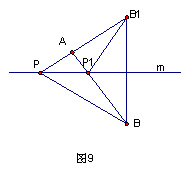
分析讨论：如图9，作出点B关于直线m的对称点B1.则直线m上任意一点P1与A、B两点距离之差等于P1A与P1B1之差. 由于点P1与A、B1不共线，点P1与 A、B1两点的距离之差总小于AB1，只有当点P1与AB1共线时，点P1与A、B1的距离之差才等于AB1.因而所求的点应为AB1与m的交点P.

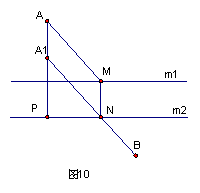
C1题：（造桥选址问题，选自人教版七年级下册）A和B两地在一条河的两岸，现要在河上造一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直.）

分析讨论：如图10，因为两平行线间的距离处处相等，所以桥长MN是不变的（与河同宽）.只须AM+BN最短. 把河岸m1连同A向下平移使两岸重合，这时A1B就是除去河宽的A到B的最短路径, 问题转化为B1题的第一种讨论。

作法：如图10，①过A作AP⊥m2 ，在AP上截取AA1=MN.

②连结A1B与m2交于N点.

③过N点作MN⊥m2与m1交于M点.

④连结AM.

则路径AMNB最短.

其实，此题将B点向上平移河宽也可以；将点A、点B同时向下、向上平移，使它们移动的距离之和为河宽也可以。同学们可以在此充分讨论。

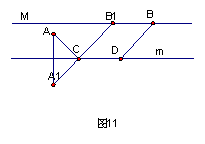
C2题：如图11，在河流m的同岸有A、B两个村庄，今欲在河岸m上确定相距a米的两点C、D，怎样才能使AC+BD最短.

分析讨论：CD=a米是固定不变的，如图11,把点B沿BM方向向左平移a米，要使AC+CD+BD最短，只要AC+CB1最短，这就同B1题的第二种讨论一样了.

作法：如右图，①过B点作BM∥m，

在BM上截取BB1=a米。

②作A点关于m的对称点A1.

③连结A1B1与m交于C点.

④在m上截取CD=a米.

⑤连结AC、BD.则所求作的AC+BD最短.

经过这样的处理，学生不再把作业当成负担，而是把作业作为一种游戏来完成，在作业的过程中，学生感觉到了相互协作的重要性，在不断地克服困难，最后解决问题的探索中，培养学生的毅力与自信心，增强学生学习数学的积极性。

通过几年的实践，笔者深切地感到，传统的教学模式与建构主义的教学模式的结合，不仅可以使学生系统的学习数学知识，打好坚实的基础，也能培养学生的数学学习兴趣，并且培养了学生不怕困难、克服困难、勇于探索的精神，许多新颖的解题方法就是在协作讨论中形成的。教师也可以从机械地布置作业、批改作业的低效劳动中解脱出来，把更多的精力花在对学生的研究、对教学方法的研究上来。不抛弃传统教育思想的先进部分，努力吸取他国的先进教育思想为我所用，应该是未来教育的发展方向。

参考文献：

1 何克抗 从Blending Learning看教育技术理论的新发展 北京师范大学现代教育技术研究所

2 赵建华 李克东 协作学习与协作学习模式 华南师范大学教育技术研究所