去年我观摩了市区青年教师大奖赛数学学科复赛阶段的参赛课,发现在三十多名选手中有五人选择了人教版课标教科书“13.2三角形全等的条件”这个课题,但他们的设计流程与方法基本上都与教师用书上的案例相同,即通过两个探究活动来得到“边边边公理”的。学生的积极性不是很高,因为他们完全是按照教师预设的思路去完成任务,没有课堂生成的东西,因此是不精彩的,细想起来,主要存在以下两个问题:
1.学生在画已知三角形三边对应相等的三角形时,感到困难,教师处理都是领着学生画,出现喧宾夺主。
2.探究“满足满足一个或两个条件时两个三角形不一定全等”时,分类及举反例验证过细,浪费了大量的时间,重心偏移。
为了克服这些不足,针对本节的重点内容探究2,我设计了以下教学过程:
教具准备:三种颜色的小木棒,长度分别为5cm,6cm,7cm;胶带。
片断:……
师:刚才我们探究得到两个三角形满足一个或两个条件时不一定全等,下面我们一起来研究当两个三角形三条边对应相等时,它们是否全等。请拿出你们手里的红、黄、蓝三种小棒,测量一下它们的长度。
(学生测量后汇报:5cm,6cm,7cm)
师:把它们首尾顺次相接,能组成三角形吗?
生:能
师:把它们用胶带固定为一个三角形。(学生动手实验)
师:你们所做的三角形有什么共同的特征?
生:三边都分别是5cm,6cm,7cm。
师:那么你们所做的任意两个三角形之间就满足了三条边对应相等,先思考一下它们是否全等,然后同桌比较,验证自己的想法。
学生对比后汇报:全等。
师:你能用一句话总结出这种现象吗?
生1:如果两个三角形的三条边分别是5cm,6cm,7cm,那么这两个三角形全等。
生2:三条边对应相等的的两个三角形全等。
师:第二个学生由一个特例猜想“三条边对应相等的两个三角形全等”,要想将它作正确的命题,也就是定理,只靠猜想是不行的,还得进进一步地验证。怎么验证呢?
思考一下:大家是如何将三根木棒连成三角形的?
请两位同学到前面演示一下。
学生用教师的教具演示:首先选择一根木棒(图中为BC),然后用另外两根木棒的一端分别与第一根木棒的两个端点相接,如图1所示。
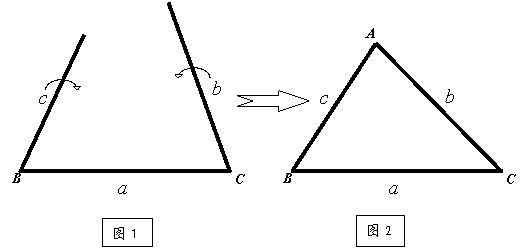 |
然后将b、c绕着相接的B、C两点旋转,使另一端重合(图上为A),最后固定。
师:很好。这两位同学是先固定了边a,然后旋转边b、c,从而得到三角形,那么在旋转过程中什么变了,什么没变?
生:b、c与a夹的角度变了,而b、c的长度没变。
师:哦,是c、b的位置变了,但它们的另一个端点到固定点B、C的距离没变。是不是相当于c、b的另一个端点在作“以B、C为圆心,以c、b为半径”的圆弧运动?……
我们的作图工具中哪一种工具可以完成这项任务?
学生:圆规。
师:不摆木棒,你可以画出长度分别为5cm、6cm、7cm的三角形吗?
生:可以,用圆规和直尺。
师:请同学们在练习本上用直尺和圆规把它做出来。
学生作图并组内交流,尝试叙述作法步骤。
师:如果将三根木棒换成三条线段,可以画出以它们为边的三角形吗?
生:可以,把它们当成木棒,也就是用圆规的两脚比出它们的长度。
师:我这里有一个三角形,同学们知道它的三条边是哪三条线段吗?能不能画出和它的三边对应相等的三角形?
(小组内合作作图,已知三角形可以自己任意画出,对照书上P95作法,规范几何语言,教师巡视辅导)。
师:把画出的三角形剪下来,与原三角形对比,看是否全等。你能得到什么结论?
生:三边对应相等的两个三角形全等。
师:这次是由特例得出的吗?
生:不是,因为我们所画的三角形都不一样,具有一定的普遍性。
……
这样做,学生通过动手分操作散了难点,并在操作过程中理解了做法的依据,增强了学生探究的兴趣,为以后学生独立获得课本知识、培养创新意识提供了一定的思路,取得了比较令人满意的效果。