参与式教学是在“以学生为中心，以活动为主，共同参与”的理念指导下，强调在教学中体现学生的主体地位的教学组织形式和教学方式。其核心就是充分调动教师和学生在教学过程中两个方面的积极性，贯彻教学民主的理念，创造师生平等、和谐的学习氛围，提高学习主体自主学习和独立思考的自觉意识，激发学生自身的潜能和创造力，在双边教学过程中突出教师的主导作用和学生的主体作用，体现以人为本的原则。近年来，笔者一直参加省立项课题“参与式教学”课题组的实践与研究工作。在教学过程中，如何引导学生积极主动参与学习过程，结合教学实际，我进行了一些有益的尝试。在这里呈上一篇“参与式教学”课例，就“数学学科中如何进行参与式教学”这一话题，与大家共同探讨，以求教于各位同行。
【课例简案】
教材版本：义务教育人教版几何第二册
课题：两圆的公切线（3）
教学目标：
1、知识获取目标：在直线与圆的位置关系、圆与圆的位置关系的变化中，综合运用所学知识深刻理解运动中的变与不变，以达到知识正确迁移的目的。
2、能力培养目标：在动手操作中，让学生对图形进行直觉猜想，通过图形变式，培养学生的发散思维能力，提高其分析问题、解决问题的能力。
3、情感孕育目标：培养学生敢于猜想的探索精神，实事求是的科学精神，勇往直前的进取精神。
教学重点：“圆”有关知识的整体梳理。
教学难点：用运动的观点理解变量与不变量。
教学方法：以“引导—探究”为主，“参与—讨论”相佐。
教学过程：
一、创设问题情境，激发参与兴趣
如图1，已知两圆相交于A、B，直线CD与两圆分别相交于C、E、F、D。
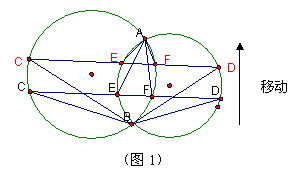
1、动手操作：用量角器量出∠EAF与∠CBD的大小。
2、直觉猜想：根据量得结果，请你猜想∠EAF与∠CBD之间存在怎样的大小关系？
3、证明结论。
（遵循学生的认知规律，培养学生大胆猜想的探索精神）
二、参与问题变式，激活思维灵性
1、当直线CD的位置向上移动至如图2所示的位置，上题的结论是否还能成立？并说明理由。
（旨在强化相交两圆中的公共弦的桥梁作用）
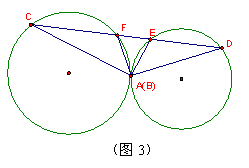
2、如果将已知中的“两圆相交”改为“两圆外切于A”，其余条件不变（如图3），那么上题中的结论将变为什么？并作出证明。（意在强调相切两圆中公切线的纽带作用）
3、若将CD继续上移，使得CD切⊙O
于C，交⊙O
于E、D（如图4）。
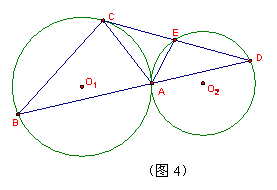
（1）找出图中一对互补的角；
（2）连接DA并延长交⊙O于B，连接CB，则还有哪些新的结论？
（通过结论的发散，打开学生的视野，达到系统获取知识的目的）
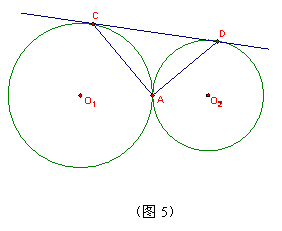
4、CD继续移动，分别切两圆于C、D（如图5），试判断△ACD的形状。
（通过解法的发散，开阔学生的思维，达到整体梳理知识的目的）
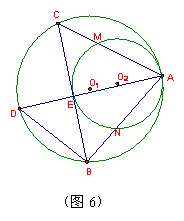
5、两圆由外切变内切。如图6，⊙O与⊙O内切于A点，⊙O的弦BC切⊙O于E点，AE的延长线交⊙O于D点，AC、AB分别与⊙O交于M、N两点。试探求图中成立的结论（可添加辅助线）。
（让学生参与到问题的结论的探索中，亲身体验成功的喜悦）
三、揭示问题规律，提炼参与成果
在直线与圆、圆与圆的位置变化中，用运动的观点正确理解“变中不变”的规律，用科学的方法构建系统的知识结构。
【评析】
本节课遵循学生的认知规律，以素质教育思想为指导，学生主动参与为前提，师生合作讨论为形式，培养学生创新精神和实践能力为目的，构建了“教师导、学生学”的互动的比较理想的教学境界。
首先，激趣引题，诱发参与。利用投影呈现两个圆的位置关系图，然后增加条件，让学生在测量、观察、比较等活动中去感知问题、形成认识、得出结论。简短的两三分钟，吸引了学生的注意力，调动了学生的情绪，形成了良好的课堂气氛的切入口，诱发了学生参与的愿望。
其次，设疑点拨，合作参与。通过直线与两圆的位置关系的逐步变动，设计了恰当的教学情境，凸现了问题的实质。“结论是否变化，怎样变化？”进而把学生的学、思、问联结在一起，面对学生的疑问，营造了良好的认知冲突。此时，学生的主体参与过程与活动过程同步展开，师生集思广益，互补思维，透彻分析，使获得的结论更清晰、更准确，使直观的感知上升为理性的认识，使学生在参与与合作中的表现需要、求知需要和发展需要得到了满足，他们学习的激情被激发起来。
第三，明理强化，实践参与。在经历运动变化后，师生合作探讨图形特征，发散求解思路，这时，学生的参与决定着活动方向，决定着活动的质量。学生通过解决这个问题，发现其中的关系，理解其中的新侧面，领悟数学的真谛。为发展学生的能力，老师放手让学生就这一典型问题，结合自己的经验，分析当前的问题情景，设计问题、提出问题。学生通过积极分析、推理，生成了新的问题，同时也获得了相应问题的解决方法，可贵的参与精神得到了质的飞跃。学生对数学知识形成了深刻的、结构化的理解，形成了自己的可以迁移的问题解决策略，而且对数学的学习形成了更为积极的兴趣、态度和信念。
综观本课例，遵循了“师生双主体”的教学原则，突出了数学思想方法的教学思路，体现了课堂教学的实验性、探索性，构建了“参与式教学”与“探究性活动”相结合的新理念，对于《新课程标准》的实施，无疑是一个大胆地尝试。