教材是中考命题的依据，任何复习资料都代替不了教材。教材能为创设数学问题、有效地考评学生提供丰富的素材，同时试题以知识为基础，贴近教材，也体现了对全体考生公平、公正的原则。通过对课本例题或习题的类比、改造、延伸和拓展，可以保证试题面向全体学生，减轻学生的课业负担，同时也是一种导向──重视教科书的作用。事实上，数学概念、定义及其性质是解决数学问题的起点和基础，基本的数学思想和数学方法，是在知识的形成过程中发展的，课本中重要的例题和习题，或者提供重要的结论，或者体现某种数学思想，或者是更高层次的数学命题的具体形式，它的延伸、转化和扩展，呈现出了丰富多彩的数学世界。所以，教材丰富的内涵也是编拟中考数学试题的源泉。本文以人教课标教材一例做一说明，旨在抛砖引玉。
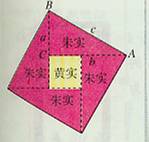
【教材内容】下图是3世纪我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”。赵爽根据此图指出：四个全等的直角三角形（红色）可以如图围成一个大正方形，中空的部分是一个小正方形（黄色）。
赵爽利用弦图证明勾股定理的基本思路如下，如图（1），把边长为
的两个正方形连在一起，它的面积是
，另一方面，这个图形可由四个全等的直角三角形（红色）和一个正方形（黄色）组成。把图（1）中左、右两个三角形移到图（2）中所示的位置，就会形成一个以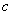
为边长的正方形（图3）。因为图（1）与图（3）都由四个全等的直角三角形（红色）和一个正方形（黄色）组成，所以它们的面积相等。因此，
。
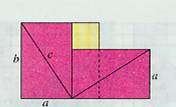
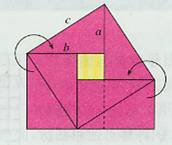
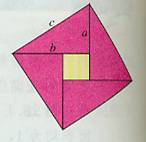
（图1） （图2） （图3）
【命题拓展】基础试题：例1、（2006年烟台）2002年8月在北京召开的国际数学家大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形。若大正方形的面积是13，小正方形的面积是1，直角三角形的较长直角边为
，较短直角边为
，则
的值为( )
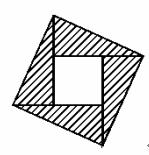
A．35 B．43 C．89 D．97
解析：本题直角三角形和正方形的性质结合在一起，考查了考生的分析能力和综合能力。
方法1：根据勾股定理和直角三角形边与边之间的数量关系求解。
根据题意得：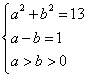
解得：
所以， =43，故选B。
方法2：根据阴影面积和直角三角形边与边之间的数量关系求解。
根据题意得：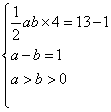
解得： 所以， =43，故选B。
拓展试题：例2、（2006年北京市中考题)请阅读下列材料：
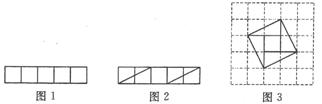
问题：现有5个边长为1的正方形，排列形式如图1，请把它们分割后拼接成一个新的正方形。
要求：画出分割线并在正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形。
小东的做法是：设新正方形的边长为 
。依题意，割补前后图形的面积相等，有
，解得
。由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长。于是，画出如图2所示的分割线，拼成如图3所示的新正方形。
请你参考小东同学的做法，解决如下问题：
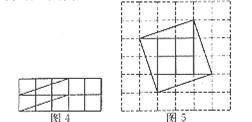
现有10个边长为1的正方形，排列形式如图4，请把它们分割后拼成一个新的正方形。
要求：在图4中画出分割线，并在图5的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形。
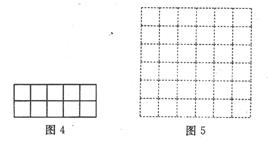
评析：本题是一道设计精良的拼图题，把面积的计算、合情的推理与动手操作结合起来，使学生思维发散能力和创造能力得到淋漓尽致的发挥，激发学生探究问题的兴趣。通过命题者的铺路搭桥、思路的引导，考生一步一步地进行深入探究，在问题解决的过程中，充分展现了考生的思维过程。
答案：所画图形如图所示
