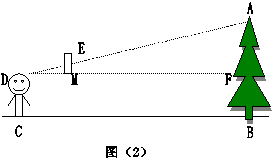学习数学课程标准发展学生思维能力

教育部制订的全日制义务教育《数学课程标准》在第一部分中指出：“……，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感态度与价值观等多方面得到进步和发展。”由此可见，培养学生的思维能力，是中学数学教学的重要任务之一，教者如何利用教材内容组织教学，探索发展学生思维能力的方法，是我们值得研究的课题。

一、联系实际，培养学生的思维能力

初中生好奇心强，观察能力和思维能力相对较差，为此，教师可根据教学要求的需要，引导学生参加实践活动，并进行积极引导，提出问题，让学生进行充分思考，认真讨论，广泛交流，共同解答。例如，在八年级学生学过相似形和解直角三角形后，可组织学生参加实践活动，为了测量校园内一棵高不可攀的大树的高度，可做如下探索：

根据物理学中光的反射定律，利用一面镜子和一根皮尺，设计如图1所示的测量方案。

把镜子放在距树AB根端B点10米的点E处， 然后沿BE方向后退到D点，恰好在镜子里看到树梢顶点A，再用皮尺量DE为3米，观察者目高CD=1.5米，试计算树AB的高度。

学生运用相似三角形的知识，很快求出了树AB的高度为5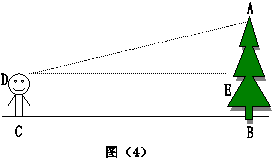米，这时教师可提问，有无其他测量树高AB的方法，同学们探索讨论思考后，纷纷发表自己的见解。

学生甲提出：如图2，可在C处用手平举刻度尺，让刻度“0”与水平线DE对齐，记下视线DA所对刻度尺位置E所示的读数，再量出BC、DC、DM的长，同样可用相似形知识求出树高AB。

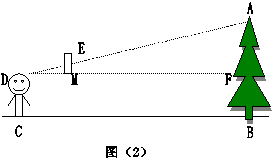
学生乙提出：如图3，可在C处用手平举刻度尺，让刻度“0”，与视线DB对齐，再记下视线DA所对刻度尺上E所示读数，再量出BC、DM、DC的长，同样可用相似形知识求出树高AB。

学生丙提出，如图4，可在C处用测角仪测得仰角∠ADE的度数，再量出BC、CD的长，可用解直角三角形的方法求得树高AB。

还有同学提出其他测算树高AB的方法，这里不一一列举。

这样让每个学生都参与探索实践活动，集思广益，培养了学生的思维能力，调动了同学们学习数学的积极性。

二、创设情境，激发学生的思维能力

众所周知，加大思维密度是优化课堂教学的重要标准，但这并不等于单纯增加几道例题和习题，倘若教者贪多求全，学生会因为在课堂上无法展开思维，只能被动地接受现成的结论，这样必然会阻碍 对学生思维能力的培养，即使遇到有思考价值的问题，也会由于教师的自行揭秘和暗示结论面失去思考的吸引力，这样的教学只能导致思维密度的下降，因此，教学中必须重视设计一些必要的停顿，关键时刻创设一些悬念，不一味追求把所有问题都讲深讲透，故意留点“空白时空”，使之产生“空白效益”，以此来诱发学生的思维活动的大力展开，让学生学有所得。例如，在讲函数时，我选了这样的例题，大拇指与小拇指尽量张开时，两指尖距离称为指距，某次实验得出如下一组数据。

(1)求出h与d之间的函数关系式；

(2)某人身高为196cm，他的指距是多少?

我在分析此题时，不急于给出函数模型，而是先启发学生先在直角坐标系中描出(19，151)、(20，160)、(21，169)、(22，178)、(23，187)这五个点，让学生发现这五点在这一条直线上，从而根据图象建模，确定为一次函数，再按一次函数的模式很快求出结果。

这样，在教学过程中留下适当空白，极大地激发了学生的求知欲，使学生的思维能力得以激发。

三、多方设疑，发展学生的思维能力

大家知道，创造思维就是从疑问和惊奇开始的，有了疑问，才能深入地思考，才能找出发人深省的问题，要让学生充分认识事物，就必须让学生对事物产生疑问，这样才能激发学生去分析思考，一味地帮助学生排难解惑的教师不是高明的老师，而高明的老师应该是不断地、巧妙地给学生提出高而可攀的要求，设置多加思考才能逾越的思维障碍，使学生的时时感到不足，又时时获得思考的乐趣，在教学过程中，教师要善于巧妙设疑，引导学生不盲从现有知识，培养学生良好的思维品质。例如，在学习完一次函数后，可安排题目：计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂有A、B两种不同规格的货车车厢共有40节，使用A型车厢每节费用为6000元，使用B型车厢每节费用8000元。

(1)设运送这批货物的总费用为y万元，这列货车挂A型车厢x节，写出y与x间的函数关系式；

(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求，安排A、B两种车厢的节数，那么共有哪几种安排车厢的台幣方案?

(3)在上述方案中，哪个方案运费最省，最少运费是多少万元?

对于问题(1)，大部分学生经思考都能顺利求得答案为y=-0.2x+32。

对于问题(2)，涉及到不得式组的整数解，学生通过思考、讨论、探索，通过努力也能求出三种方案：即①A型24节、B型16节；②A型25节、B型15节；③A型26节，B型14节。

对于问题(3)，根据一次函数的性质，结合(2)中的方案，得出方案③运费最省的26.8万元。

这样让学生参与讨论，激发学生的求知欲，又联系实际，学生的主体活动得以体现，思维能力得以发展，解决实际问题的能力有了提高。

四、改编习题，提高学生的思维能力

新课改的目标之一就是要提高学生的兴趣，变“要我学”为“我要学”，这“要我学”是一种被动的学习，就有做不完的题目，而“我要学”是自主学习，题目就不够做，改编习题能使学生通过思维，从做学习的奴隶中解救出来，成为学习的主人。例如，在复习一元二次方程根的判别式的应用时，可出示如下题目：当k为何值时，关于x的一元二次方程2x2-3x+(k-5)=0没有实数根?

学生经过思考后求出答案为“k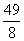＞”，随后教师要求学生做完后，每人根据原题至少改编一个题目进行交流。

学生甲编出：“当k为何值时，关于x的二次三次式2x2-3x+(k-5)在实数范围内不能分解为两个一次因式的积?”

学生乙编出：“当k为何值时，关于x的不等式2x2-3x+(k-5)＞0的解集为一切实数?”

学生丙编出：“当k为何值时，函数 y=2x2-3x+(k-5)与x轴没有交点?”

这样，通过学生自编习题，加深了对所学知识的理解，增强了学生学习数学的兴趣，提高了学生的思维能力。