初中数学课程标准(实验稿)的正式颁布给数学教育改革注入了新的生机,由于中考是现行体制下初中数学的指挥棒,所以必将折射出课程标准的最新内涵和动向,同时中考的发展趋势也是促进基础教育课程改革的一大动力。我们知道,现行的数学中考题已经或多或少地反映了课程改革的内容,出现越来越多的新题型,具有探究性、实践性、创新性等特点,课程标准强调以学生发展为本,特别重视发挥学习主体在认识活动中的主动和能动作用,面对全新的教育理念,我们想得更多的是课程标准下新的教学思想会给近几年的中考带来什么样的影响。笔者结合近年来的中考题,谈点自己的看法。
1 开放性问题可促进学生个性的培养
课程标准强调要关注学生的个性差异,有效地实施有差异的教学,使每个学生都得到充分的发展,面对全体学生多样化的学习需求,开放性问题能较好地达到这一要求,学生需要通过一系列分析,展开发散性思维,运用所学的知识经过推理,得出正确的结论,充分显示出思维的多样性,同时也体现了学生对数学学习的个性化,从而全方位地培养了学生的创造能力。
例1 试比较下面两个几何图形的异同,请分别写出它们的两个相同点和两个不同点。
例如:相同点:正方形的对角线相等,正五边形的对角线也相等。
不同点:正方形是中心对称图形,正五边形不是中心对称图形。
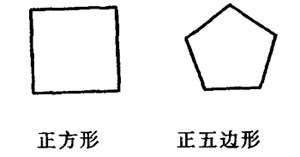
(金华市2002年中考题)
相同点:_________;(2)_________
不同点:(1)_________;(2)_________
这类开放性问题不同于在固定条件下研究固定结论,可以鼓励学生从多角度、多层次、多侧面地思考问题,发展学生的求异思维,对于激发学生的学习兴趣,发挥学生的主体精神,培养学生的个性很有益处。
因此,学生在学习过程中通过开放性问题经历适当的数学交流活动,让他们感受到别人的思维方式和思维过程。以改变自己在认知上的单一性,从而达到个性良性发展的目的。
2 操作性问题可强化学生的动手能力
课程标准指出有效的数学学习活动不能单纯地依赖模仿与记忆,动手操作也是学生学习数学的一种重要方式。欧、美等国提倡学生在"做数学"中学数学,充分体现了以学生为主体,让学生主动参与教学活动中进行的。课程标准下的新教材非常重视学生活动的开展,尤其重视操作能力的培养,因为它具备知识综合性强、趣味性强、容量大等特性。让学生在多样化的操作活动中体验数学,如利用户外测量活动、制作活动、利用实物探索数量和图形的活动等。新教材七年级已把实践操作纳入其中,如利用易得的包装盒,让学生动手操作,了解图形在"展开与折叠"过程中的变化,亲自发现结果的来龙去脉和可靠性,改变以往的灌输式教学,留给学生一个活动和探索的空间。
例2 在平面内,分别用3根、5根、6根…火柴首尾依次相接,能搭成什么形状三角形呢?通过尝试,列表如下:
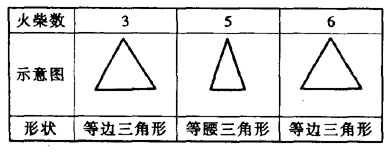
(1)4根火柴能搭成三角形吗?
(2)8根、12根火柴能搭成几种不同形状三角形?并画出它的示意图。
(2002年福建宁德中考题)
这类题型主要以学生熟悉的、感兴趣的图形为背景提供观察和操作的机会,让学生通过动手操作,亲自发现结果的准确性,在思想上和行动上逐步消除理论和实践之间的阻隔。所以,我们在平时的教学中要向学生提供充分从事数学活动的机会,积极引导学生从事实验活动和实践活动,培养学生乐于动手的意识。
3 应用性问题可提高学生的实践能力
尽管我国中学生在国际奥林匹克数学竞赛中连获总分第一,在1992年国际教育进展评估(IAEP)的测试中也名列总分第一,但在简单应用题方面的得分率较低,仅据第九。另据调查,初中毕业生中半数不理解利润,看不懂股票走势图,弄不清统计图,不会填银行票据,更不会计算分期付款与一次性付款的利息问题。究其原因是在校内外学做家庭理财和参与社会服务的机会太少了。新课程标准重视数学学习与实践的结合,重视考查学生在面对真实情境下,解决问题的能力,从而引导学生关注对应用性问题的领悟能力和解决能力。
例3 哈尔滨市移动通讯公司开设了两种通讯业务:"全球通"使用者先缴50元月基础费,然后每通话1分钟,再付电话费0.4元;"神州行"不缴月基础费,每通话1分钟,付话费0.6元(这里均指市内通话)。若一个月内通话x分钟,两种通讯方式的费用分别为y1元和y2元。
(1)写出y1、y2与x之间的函数关系式;
(2)一个月内通话多少分钟,两种通讯方式的费用相同;
(3)若某人预计一个月内使用话费200元,则应选择哪种通讯方式较合算?
(哈尔滨市2002年中考题)
这类题型旨在利用与生活实际有关的具体情境,注重学生的心理历程,搭起数学与实际问题的桥梁,协助学生体验由生活情境中抽象出的数学问题,即学会运用数学建模思想方法,培养学生用数学的观点和方法来考察周围的事物,提高了学生应用数学的能力。本问题最终归结为一个函数模型,函数思想是最成功、最典型的初等模型之一。
因此,新教材带给了学生深广的发展空间,转变了教师教学观念,通过数学建模将数学与应用问题紧紧地结合起来,对培养学生的问题意识、应用意识和探究意识,让学生主动关注身边的实际问题,应该说是开辟了一条行之有效的佳径。
4 探索性问题可增强学生的分析能力
课程标准从以往比较单一的教学方法,发展到引导教师形成开放性、创新性的教学方式,体现主体性、反思性和合作性等教学思想,要求学生学会"问题—探究—发现—推广",这就把学生推理能力的培养有机地融合在数学教学的过程中,通过学生熟悉的生活发展学生的探索能力,让学生自己"悟出"道理、规律和思考方法等,学生经历操作、观察、猜想、证明的过程,做到合情推理与演绎推理相结合。在新教材中,七年级的代数式中已经把探索规律放入课程,数与式的规律寻找在历年来的中考中都有所体现。
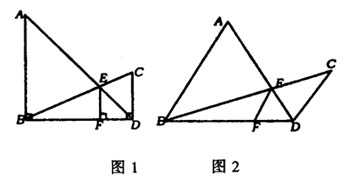
例4 已知:如图1,AB⊥BD,CD⊥BD,垂足分别为B,D,AD和BC相交于E,EF⊥BD,垂足为F.我们可以证明成立(不要求证明)。若将![]() 图1中的垂直改为斜交,如图2,AB∥CD,AB,BC相交于点E,过点E作EF∥AB,交BD于点F,则
图1中的垂直改为斜交,如图2,AB∥CD,AB,BC相交于点E,过点E作EF∥AB,交BD于点F,则
(1)![]() 还成立吗?如果成立,请给出证明,如果不成立,请说明理由:
还成立吗?如果成立,请给出证明,如果不成立,请说明理由:
(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明。
(2002年黄冈市中考题)
这类题型主要通过学生的观察、分析、探索、猜测、推理、验证等一系列探究活动,从不同的角度和层次来分析和解决问题。另外,如专题探索、图表识别和量化等在新教材中已得到了广泛运用,因此平常要注重研究探索性问题,以培养学生的分析能力。
5 阅读理解题可加强学生的自学能力
课程标准重视培养学生的自学能力,强调了油價学习方法的指导,学会学习,重视发现、形成知识的过程而不仅仅是结果。这就要求学生在获取知识的过程中,教师不要灌输式地把知识交给学生,而是引导学生通过自己思考或自学来获得,将课本知识转化为个人能力,加强了学生的必备知识。因此,要对学生基础概念、思维能力、理解能力、运用数学语言能力等的考查,可借助阅读理解题能很好地达到上述要求。
例5 阅读下面短文
如图3,△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第3个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB(如图4),解答问题:
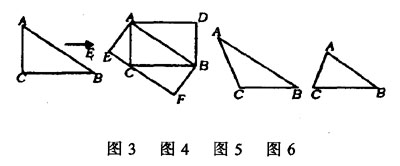
(1)设图4中矩形ACBD和矩形AEFB的面分别为S1,S2,则S1________S2(填:">","="或"<")。
(2)如图5,△ABC是钝角三角形,按短文中要求把它补成矩形,那么符合要求的矩形可以画________个,利用图5把它画出来。
(3)如图6,△ABC是锐角三角形且三边满足BC>AC,按短文中的要求把它补成矩形,那么符合要求的矩形可以画________个,利用图6把它画出来。
(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?
(2002年陕西省中考题)
这类题型主要通过分析、比较、抽象和概括等数学手段,运用已学过的数学知识和数学方法,对知识进行归纳总结,迁移应用,善于联想猜想,借鉴创新,它能很好地培养学生的自学能力。
6 跨学科问题可提升学生的综合能力
课程标准要求教学与信息社会发展的总体趋势相适应,着眼于学生全面、持续、和谐地发展,强调科际联系,要求研究和把握学科之间知识、技能的迁移和横向联系,研究和把握知识的局部和整体之间的关系,注重学科内的综合和学科间的整合,再加上先进的技术手段,才能形成解决世纪难题的有效方案。因此,数学教学也不能仅仅关注数学知识之间的联系,还要关注数学与现实世界、其他学科之间的联系,如通过在数学试题中穿插自然学科知识,就可以培养学生综合理科能力。跨学科问题能考查学生的综合能力,在中考中会有所体现。
例6 我们知道,溶液的酸碱度由pH值确定,当pH>7时,溶液呈碱性;当pH<7时,溶液呈酸性。若将给定的HC1溶液加水稀释,那么在下列图像中,能反映HCl溶液的pH与所加水的体积(V)的变化关系的是:
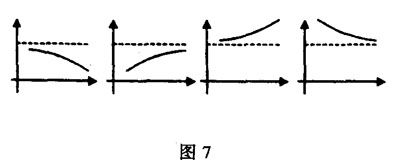
(2002年安徽省中考题)
这类题型主要是考查学生对各科知识的整体性和综合性的认识,除了要考查学生函数图象上的一些纯数学知识外,还渗透了自然中的酸碱度的变化,同时突出了数学应用的广泛性,突出了数学作为工具学科的本质。
随着数学课程改革的深入,中考也将会适应数学教学改革的要求,重视新教材、新理念,除了注重对最基本的知识和技能的考查之外,还会适当增加一些灵活性试题,重视学生个性和创造性思维能力的培养,鼓励学生进行探索,拓展思路,会出现应用和探究能力,真正起到考查学生学习数学的潜能的目的。总之,准确地把握数学课程标准的新理念,吸收新思想,将有助于提高数学教学水平,有助于研究数学中考的发展方向。
参考文献
[1]数学课程标准研制组编写。数学课程标准(实验稿)解读。北京大学出版社,2002.
[2]周卫勇主编。走向发展性课程评价。北京大学出被社,2002.
[3]靳玉乐等主编。新教材将会给教师带来些什么,北京大学出版社,2002.
[4]钟启泉主编。新教材师资培养精要。北京大学出版社,2002.