《数学课程标准》指出：“动手实践、自主探索与合作交流是学生学习数学的重要方式。”强调学生的创新意识是在主动探索知识的过程中得到培养的，学生的实践能力是在运用知识解决问题的实践活动中得到发展的，课堂教学应该是培养学生创新意识和实践能力的主阵地。因此，进行初中数学探究性学习的课堂教学实践，寻找与时代发展相适应的教与学的方式势在必行。
所谓数学探究性学习，是指“学生在数学领域或现实生活的情境中，通过发现问题、调查研究、动手操作、表达与交流等探究性活动，获得知识、技能和态度的学习方式和学习过程。”如何在初中数学教学中引导学生进行探究性学习？本文试图通过例子，展示探究性学习的课堂教学设计，就教于方家。
例题：已知
中，AB＝AC，D为BC边所在直线上任一点，
于E，于F。试求DE与DF满足的关系。
本题没有提供图形，而且DE与DF满足怎样的关系不清楚，学生感到难以人手。如何激发学生的探究欲望，让他们自己来参与数学发现呢？为此，进行以下的教学设计：
一、创设情境，明确探究目标
在《几何画板》中用鼠标拖动相关关键点结合“计算工具" 演示：等腰三角形中，DE与DF的和始终是一个固定的值。激起学生疑问：点D、E、F的位置在不断变化，为什么它们的和却始终不变呢？这个固定的值是多少呢？与什么有关呢？如何来证明呢？
二、动手操作，深入探究
1、引导学生正确分类。
（1)你认为点D的位置可能有几种情况？（三种：点D在B、C之间或与B、C之一重合或在BC的延长线上）
(2)等腰三角形有几种类型？（锐角、直角、钝角等腰三角形）你认为哪一种情形最特殊？（等腰直角三角形）
2、从特例人手，逐类考查。
在等腰直角三角形中（图1）：
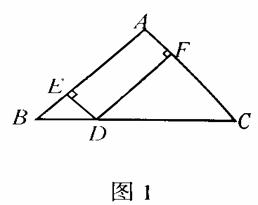
（1）当点D与B、C之一重合时，DE与DF应满足什么关系？请进行合理猜想。（等于腰长，很容易验证。）
(2)当D在B、C之间时，上述猜想还成立吗？你能就此种情形验证你的猜想吗？
3、从特殊向一般转化，探究普遍规律。
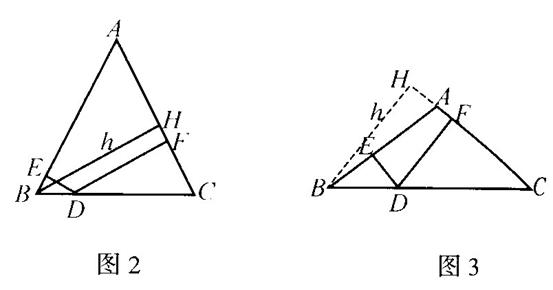
（1）从特殊到一般地推广，若将等腰直角三角形改为锐角等腰三角形或钝角等腰三角形，上述猜想是否仍旧成立？若不成立，是否有类似的结论？请作出合理猜想。（DE与DF之和等于腰上的高线长）。（图2、图3)
(2）如何验证（1）中的猜想？（用截短法、加长法或面积法）
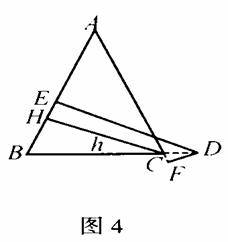
（3）当点D在BC的延长线上时，DE与DF又将满足什么样的关系？如何证明？（图4)
三、群体参与、合作交流
1、以四人为小组，进行组内合作，充分发表己见，形成小组集体意见。
2、进行组际交流，交流猜想结论、交流验证方法等。
3、学生概括题中DE与DF在不同情况下满足的不同关系。
说明：这里，教师设计了一个容易激疑的问题情境，给学生思维以方向和动力；五个由浅人深的问题引起学生深人的思考，并且能促使学生“发现问题，作出思考，提出猜想，进行验证”等探究性的学习活动，并教给学生探究性学习的方法。这样设计探究学习活动，是为了更有利于学生主体性的发挥。在探究活动中强调合作，促进了学生在思维品质、人格特征以及解题方法等方面的优势互补，使学生兴趣盎然地投人探究新知的学习活动。
四、反思小结、提炼数学思想
1、在问题的解决过程中，我们是怎样人手的？为什么要这样分类？（根据点D在等腰三角形底边上的位置和三角形的形状分类；在无图形的几何问题中往往需分情形分类讨论）
2、在证明过程中我们主要运用了哪两种方法？哪一种方法更加优越？（面积法较简捷）
3、本题可以概括出怎样的一般性的结论？（等腰三角形底边上任意一点到两腰的距离之和（之差）等于腰上的高线长）
4、在解题过程中运用了哪些数学思想方法？（整体思想、分类讨论的思想、从特殊到一般的思想等。）
五、类比迁移、引申拓广
应用本题的解题方法和结论，尝试解决下列问题：
问题l：如图5，在矩形ABCD中，AC、BD交于O，P为AD上任一点，
于点E，
于点F。
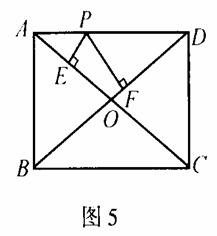
1、若AB＝3，BC=4。求PE十PF的值。
2、若AB＝a，BC=b。求PE＋PF的值。
3、若AB＋BC＝8，求PE＋PF的最大值。
反思：本题和上述例题有何联系吗？（题中包含例题中的基本图形，如图6)
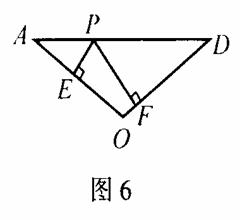
问题2：如图7，正 的边长为2，AD是BC边上的高线，点P为AD上任意一点，求PD＋PE＋PF的值。
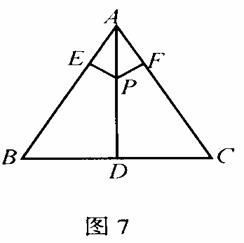
本题作为一种特殊情形，很容易求出PD十PE＋PF的值就是高线AD的长。
以此题为背景，引导学生猜想并验证下列结论：
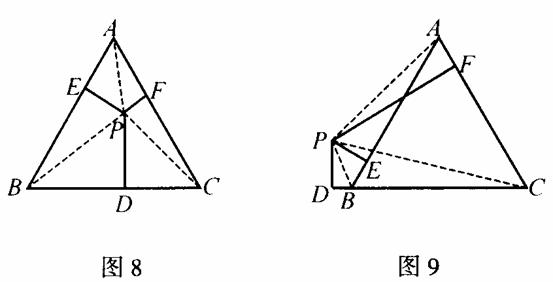
1、当点P为正 内任意一点时，求PD十PE十PF的值。（如图8)
2、当点P为正△ABC外任意一点时，求PD、PE、PF三者满足的关系。（如图9)
分析：
1、如图8，连结AP、BP、CP，则
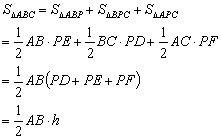
所以PD十PE+PF=h（这里h是正三角形的高线长，下同）
2、应分成以下三种情况进行讨论。
(1)当点P在一边和另两边的反向延长线所围成的区域内时，如图9，连结AP、BP、CP，则
。
即 
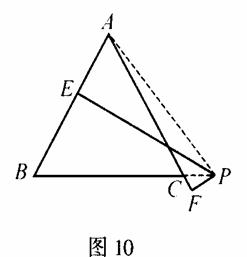
(2）当点P在一边的延长线上时，如图10，同法可推出PD＋PE一PF＝h（此时PD=0).
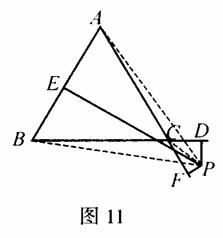
(3）当点P在某两边延长线所夹角的内部时，如图11，同法可得PE一PD一PF＝h
说明：学生经过自己的主动探索、实验，发现了重要的结论，这是对学生主动参与精神的激励，能使学生体验到主动探究成功后的喜悦，增强学生学习的动力和信心。经过组内和组际的交流，能使学生各自得到不同的收获，同时能使学生感悟到“面对新问题，联想旧知识，寻找新旧知识之间的关系，揭示知识规律，获取新知”的探究方法和策略，使他们更自觉更主动地投入到探究性学习活动中去。
实施数学探究性学习，是数学教学和学习方式改革的必由之路。学生探究性学习活动能否顺利实施，关键在于教师能否创造适宜的教学情境和进行合理的引导。在新课程实施过程中，教师要运用一切可能的手段，不断优化教学设计，激发学生的学习兴趣，创设有效的探究时间和空间，形成良好的探究风气，让每个学生都有主动探究的机会和欲望，从而真正实现“不同的人在数学上得到不同的发展”。